标签:
本篇用双向链表和模拟栈混洗过程两种解答方式具体解答“栈混洗”的应用问题
有关栈混洗的定义和解释在此篇:手记-栈与队列相关
Figure 1 shows the structure of a station for train dispatching.
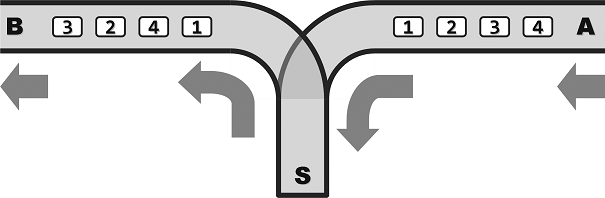
Figure 1
In this station, A is the entrance for each train and B is the exit. S is the transfer end. All single tracks are one-way, which means that the train can enter the station from A to S, and pull out from S to B. Note that the overtaking is not allowed. Because the compartments can reside in S, the order that they pull out at B may differ from that they enter at A. However, because of the limited capacity of S, no more that m compartments can reside at S simultaneously.
Assume that a train consist of n compartments labeled {1, 2, …, n}. A dispatcher wants to know whether these compartments can pull out at B in the order of {a1, a2, …, an} (a sequence). If can, in what order he should operate it?
Two lines:
1st line: two integers n and m;
2nd line: n integers separated by spaces, which is a permutation of {1, 2, …, n}. This is a compartment sequence that is to be judged regarding the feasibility.
If the sequence is feasible, output the sequence. “Push” means one compartment goes from A to S, while “pop” means one compartment goes from S to B. Each operation takes up one line.
If the sequence is infeasible, output a “no”.
Input
5 2
1 2 3 5 4
Output
push
pop
push
pop
push
pop
push
push
pop
pop
Input
5 5
3 1 2 4 5
Output
No
1 <= n <= 1,600,000
0 <= m <= 1,600,000
Time: 2 sec
Memory: 256 MB
某列车调度站的铁道联接结构如Figure 1所示。
其中,A为入口,B为出口,S为中转盲端。所有铁道均为单轨单向式:列车行驶的方向只能是从A到S,再从S到B;另外,不允许超车。因为车厢可在S中驻留,所以它们从B端驶出的次序,可能与从A端驶入的次序不同。不过S的容量有限,同时驻留的车厢不得超过m节。
设某列车由编号依次为{1, 2, ..., n}的n节车厢组成。调度员希望知道,按照以上交通规则,这些车厢能否以{a1, a2, ..., an}的次序,重新排列后从B端驶出。如果可行,应该以怎样
的次序操作?
共两行。
第一行为两个整数n,m。
第二行为以空格分隔的n个整数,保证为{1, 2, ..., n}的一个排列,表示待判断可行性的驶出序列{a1,a2,...,an}。
若驶出序列可行,则输出操作序列,其中push表示车厢从A进入S,pop表示车厢从S进入B,每个操作占一行。
若不可行,则输出No。
见英文题面
1 ≤ n ≤ 1,600,000
0 ≤ m ≤ 1,600,000
时间:2 sec
空间:256 MB
双向链表
用链表解题的关键其实就在设立一个*P指向A栈顶元素,每一次比对p和p的上一个元素,若能够匹配则删除该元素,并将指针指向该元素的下一个元素,也就是说如果匹配p,则p = p->next,如果匹配p的上一个元素则不动。
这里的p和p的上一个元素其实就是模拟A栈顶元素和S栈顶元素,这里的时间度为O(n)。
具体如下:

1 // 1-n编号车厢按照“栈混洗”从A->S->B,最终确认车厢在B处是否可以按照某一序列排列 2 // 一种栈结构-输出不要用strcat进行字符链接输出(会TLE) 3 // 双向链表模拟 4 // Memory:70984 Time:1753Ms(按最大样例) 5 #include<iostream> 6 #include<cstring> 7 #include<cstdio> 8 using namespace std; 9 10 #define MAX 1600005 11 12 // A->S->B 13 /*构造双向链表*/ 14 struct Train{ 15 int num; 16 Train *up; 17 Train *down; 18 Train(){}; 19 Train(int n) :num(n){}; 20 }*header,*tailer; //前后哨兵 21 22 int target[MAX]; 23 bool output[2 * MAX]; //true为push,false为pop 24 int k; //输出操作数 25 26 /*构建*/ 27 void Creat_Train(int n) 28 { 29 header = new Train(0); 30 header->up = NULL; 31 32 Train *rear = header; //定义尾针 33 for (int i = 1; i <= n; i++) 34 { 35 Train *p = new Train(i); //新链表元素 36 rear->down = p; 37 p->up = rear; 38 39 rear = p; 40 } 41 tailer = new Train(0); 42 rear->down = tailer; 43 tailer->up = rear; 44 tailer->down = NULL; 45 } 46 47 /*删除*/ 48 void Delete(Train *p) 49 { 50 p->up->down = p->down; 51 p->down->up = p->up; 52 delete p; 53 } 54 55 int main() 56 { 57 int n, m; 58 scanf("%d%d", &n, &m); 59 for (int i = 1; i <= n; i++) //目标序列 60 scanf("%d", &target[i]); 61 62 Creat_Train(n); 63 64 int counter = 0; //S站车厢数量 65 Train *cur = header->down; 66 /*开始匹配第i个目标车厢*/ 67 for (int i = 1; i <= n; i++) 68 { 69 if (cur->num == target[i]) //A栈顶匹配 70 { 71 Train *tmp = cur; 72 cur = cur->down; 73 Delete(tmp); //删除车厢结点 74 if (counter + 1 > m) //S滞留车厢过多 75 { 76 printf("No\n"); 77 return 0; 78 } 79 output[k++] = true; 80 output[k++] = false; 81 } 82 else if (cur->up->num == target[i]) //S栈顶匹配 83 { 84 Delete(cur->up); 85 output[k++] = false; 86 counter--; 87 } 88 else{ //A->S 89 cur = cur->down; 90 --i; 91 counter++; 92 if (cur->down == NULL || counter > m) //A空 Or S滞留车厢过多 93 { 94 printf("No\n"); 95 return 0; 96 } 97 output[k++] = true; 98 } 99 } 100 /*Output*/ 101 for (int i = 0; i < k; i++) 102 { 103 if (output[i]) 104 printf("push\n"); 105 else printf("pop\n"); 106 } 107 108 return 0; 109 }
模拟栈混洗过程
也就是设立三个栈,模拟车厢进栈,出栈的过程,时间度也是O(n)。
TshingHua OJ 中不允许使用STL,所以自己用数组模拟了stack。
具体如下:

1 // 1-n编号车厢按照“栈混洗”从A->S->B,最终确认车厢在B处是否可以按照某一序列排列 2 // 一种栈结构-输出不要用strcat进行字符链接输出(会TLE) 3 // 模拟栈混洗过程 4 // Memory:41332 Time:1562Ms(按最大样例) 5 #include<iostream> 6 #include<cstring> 7 #include<cstdio> 8 using namespace std; 9 10 #define MAX 1600005 11 12 // A->S->B 13 int A[MAX], S[MAX], B[MAX]; //数组模拟栈 14 int curA, curS; //A和S当前栈顶 15 bool output[7 * MAX]; //true为push,false为pop 16 int k; //输出操作数 17 18 int main() 19 { 20 int n, m; 21 scanf("%d%d", &n, &m); 22 for (int i = 1; i <= n; i++) //目标序列 23 scanf("%d", &B[i]); 24 for (int i = n; i >= 1; i--) //Init现有序列 25 A[n - i + 1] = i; 26 curA = n; 27 curS = 0; 28 29 /*从栈顶开始匹配栈B*/ 30 for (int i = 1; i <= n; i++) 31 { 32 if (S[curS] == B[i]) //S栈顶匹配 33 { 34 curS--; //S出栈 35 output[k++] = false; 36 } 37 else if (A[curA] == B[i]) //A栈顶匹配 38 { 39 --curA; //A出栈 40 output[k++] = true; 41 output[k++] = false; 42 if (curS + 1 > m) //S爆栈 43 { 44 printf("No\n"); 45 return 0; 46 } 47 } 48 else{ 49 S[++curS] = A[curA--]; //A->S(A出栈-S入栈) 50 output[k++] = true; 51 i--; 52 if (!curA || curS > m) //A栈空 or S爆栈 53 { 54 printf("No\n"); 55 return 0; 56 } 57 } 58 } 59 /*output*/ 60 for (int i = 0; i < k; i++) 61 { 62 if (output[i]) 63 printf("push\n"); 64 else printf("pop\n"); 65 } 66 67 return 0; 68 }
ACM/ICPC 之 用双向链表 or 模拟栈 解“栈混洗”问题-火车调度(Tshing Hua OJ - Train)
标签:
原文地址:http://www.cnblogs.com/Inkblots/p/4950331.html