标签:

#include <bits/stdc++.h> const int MAX=1010; char x[MAX]; char y[MAX]; int DP[MAX][MAX]; int b[MAX][MAX]; using namespace std; int PRINT_LCS(int b[][MAX],char *x,int i,int j) { if(i==0||j==0) return 1; if(b[i][j]==1) { PRINT_LCS(b,x,i-1,j-1); cout<<x[i]<<" "; } else if(b[i][j]==2) { PRINT_LCS(b,x,i-1,j); } else if(b[i][j]==3) { PRINT_LCS(b,x,i,j-1); } } int main() { int T; int n,m,i,j; cin>>T; while(T--) { while(cin>>n>>m) { for(int i=1; i<=n; i++) cin>>x[i]; for(int j=1; j<=m; j++) cin>>y[j]; memset(DP,0,sizeof(DP)); for(i=1; i<=n; i++) { for(j=1; j<=m; j++) { if(x[i]==y[j]) { DP[i][j]=DP[i-1][j-1]+1; b[i][j]=1; } else if(DP[i-1][j]>=DP[i][j-1]) { DP[i][j]=DP[i-1][j]; b[i][j]=2; } else { DP[i][j]=DP[i][j-1];//Max(DP[i-1][j],DP[i][j-1]); b[i][j]=3; } } } cout<<DP[n][m]<<endl; PRINT_LCS(b,x,n,m); cout<<endl; } } return 0; }
mon Subsequence)。其定义是,一个序列 S ,如果分别是两个或多个已知序列的子序列,且是所有符合此条件序列中最长的,则 S 称为已知序列的最长公共子序列。而最长公共子串(要求连续)和最长公共子序列是不同的
动态规划
第一步:先计算最长公共子序列的长度。
第二步:根据长度,然后通过回溯求出最长公共子序列。
现有两个序列X={x1,x2,x3,...xi},Y={y1,y2,y3,....,yi},
设一个C[i,j]: 保存Xi与Yj的LCS的长度。
递推方程为:
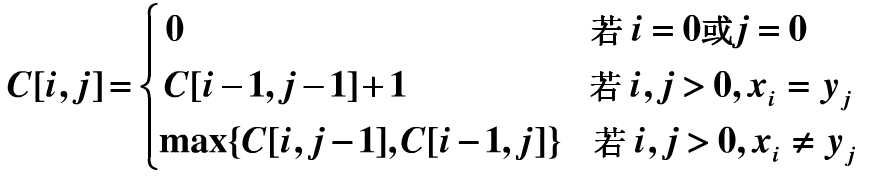
代码亲测:
LCS(Longest Common Subsequence 最长公共子序列)
标签:
原文地址:http://www.cnblogs.com/zpfbuaa/p/4953865.html