标签:
潜在语义分析通过矢量语义空间来分析文档和词的关系。
基本假设:如果两个词多次出现在同个文档中,则两个词在语义上具有相似性。
LSA使用大量文本构成矩阵,每行表示一个词,一列表示一个文档,矩阵元素可以是词频或TF-IDF,然后使奇异值分解SVD进行矩阵降维,得到原矩阵的近似,此时两个词的相似性可通过其向量cos值。
降维原因:
- 原始矩阵太大,降维后新矩阵是原矩阵的近似。
- 原始矩阵有噪音,降维也是去噪过程。
- 原始矩阵过于稀疏
- 降维可以解决一部分同义词与二义性的问题。
推导:
对于文档集可以表示成矩阵X,行为词,列为文档
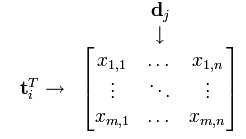
词向量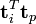 的点乘可以表示这两个单词在文档集合中的相似性。矩阵
的点乘可以表示这两个单词在文档集合中的相似性。矩阵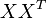 包含所有词向量点乘的结果
包含所有词向量点乘的结果
降维的过程其实是奇异值分解,矩阵X可分解成正交矩阵U、V,和一个对角矩阵 的乘积
的乘积

因此,词与文本的相关性矩阵可表示为:
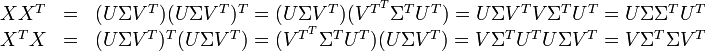
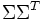 与
与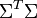 是对角矩阵,因此
是对角矩阵,因此 肯定是由
肯定是由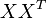 的特征向量组成的矩阵,同理
的特征向量组成的矩阵,同理 是
是 特征向量组成的矩阵。
特征向量组成的矩阵。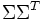 中的元素。综上所述,这个分解看起来是如下的样子:
中的元素。综上所述,这个分解看起来是如下的样子: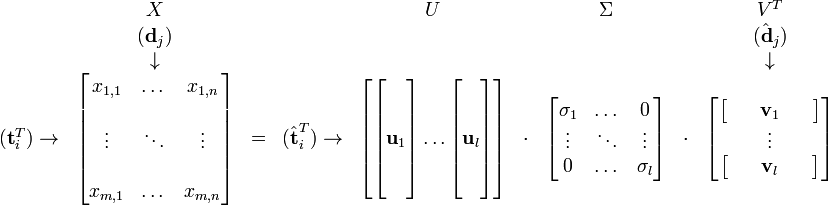
 被称作是奇异值,而
被称作是奇异值,而  和
和 则叫做左奇异向量和右奇异向量。
则叫做左奇异向量和右奇异向量。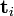 只与U矩阵的第i行有关,我们则称第i行为
只与U矩阵的第i行有关,我们则称第i行为  。
。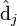 只与
只与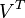 中的第j列有关,我们称这一列为
中的第j列有关,我们称这一列为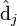 。
。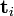 与
与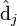 并非特征值,但是其由矩阵所有的特征值所决定。
并非特征值,但是其由矩阵所有的特征值所决定。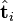 与含有k个奇异值的矩阵相乘,实质是从高维空间到低维空间的一个变换,可以理解为是一个高维空间到低维空间的近似。
与含有k个奇异值的矩阵相乘,实质是从高维空间到低维空间的一个变换,可以理解为是一个高维空间到低维空间的近似。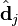 也存在这样一个从高维空间到低维空间的变化。这种变换用公式总结出来就是这个样子:
也存在这样一个从高维空间到低维空间的变化。这种变换用公式总结出来就是这个样子: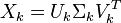
 与
与  在低维空间的相似度。比较向量
在低维空间的相似度。比较向量 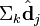 与向量
与向量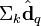 (比如使用余弦夹角)即可得出。
(比如使用余弦夹角)即可得出。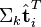 与
与 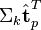 可以判断词
可以判断词 和词
和词 的相似度。
的相似度。 
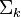 的逆矩阵可以通过求其中非零元素的倒数来简单的得到。
的逆矩阵可以通过求其中非零元素的倒数来简单的得到。 将其映射到语义空间,再与文档进行比较。
将其映射到语义空间,再与文档进行比较。低维的语义空间可以用于以下几个方面:
LSA的一些缺点如下:
摘自:http://blog.csdn.net/roger__wong/article/details/41175967
标签:
原文地址:http://www.cnblogs.com/IvanSSSS/p/4958601.html