Matlab 形态学图像处理（转载）

%% 第9章 形态学处理

%% imdilate膨胀
clc
clear

A1=imread(‘.\images\dipum_images_ch09\Fig0906(a)(broken-text).tif‘);
info=imfinfo(‘.\images\dipum_images_ch09\Fig0906(a)(broken-text).tif‘)
B=[0 1 0
   1 1 1
   0 1 0];
A2=imdilate(A1,B);%图像A1被结构元素B膨胀
A3=imdilate(A2,B);
A4=imdilate(A3,B);

subplot(221),imshow(A1);
title(‘imdilate膨胀原始图像‘);

subplot(222),imshow(A2);
title(‘使用B后1次膨胀后的图像‘);

subplot(223),imshow(A3);
title(‘使用B后2次膨胀后的图像‘);

subplot(224),imshow(A4);
title(‘使用B后3次膨胀后的图像‘);
 27%imdilate图像膨胀处理过程运行结果如下：


%% imerode腐蚀
clc
clear
A1=imread(‘.\images\dipum_images_ch09\Fig0908(a)(wirebond-mask).tif‘);
subplot(221),imshow(A1);
title(‘腐蚀原始图像‘);

%strel函数的功能是运用各种形状和大小构造结构元素
se1=strel(‘disk‘,5);%这里是创建一个半径为5的平坦型圆盘结构元素
A2=imerode(A1,se1);
subplot(222),imshow(A2);
title(‘使用结构原始disk(5)腐蚀后的图像‘);

se2=strel(‘disk‘,10);
A3=imerode(A1,se2);
subplot(223),imshow(A3);
title(‘使用结构原始disk(10)腐蚀后的图像‘);

se3=strel(‘disk‘,20);
A4=imerode(A1,se3);
subplot(224),imshow(A4);
title(‘使用结构原始disk(20)腐蚀后的图像‘);
%图像腐蚀处理过程运行结果如下：


%% 开运算和闭运算
clc
clear
f=imread(‘.\images\dipum_images_ch09\Fig0910(a)(shapes).tif‘);
%se=strel(‘square‘,5‘);%方型结构元素
se=strel(‘disk‘,5‘);%圆盘型结构元素
imshow(f);%原图像
title(‘开闭运算原始图像‘)
 61%运行结果如下：


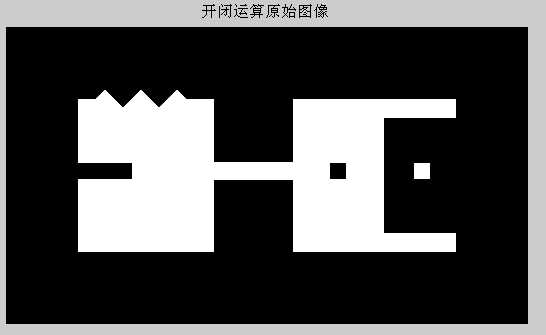%开运算数学上是先腐蚀后膨胀的结果
%开运算的物理结果为完全删除了不能包含结构元素的对象区域，平滑
%了对象的轮廓，断开了狭窄的连接，去掉了细小的突出部分
fo=imopen(f,se);%直接开运算
figure,subplot(221),imshow(fo);
title(‘直接开运算‘);

%闭运算在数学上是先膨胀再腐蚀的结果
%闭运算的物理结果也是会平滑对象的轮廓，但是与开运算不同的是，闭运算
%一般会将狭窄的缺口连接起来形成细长的弯口，并填充比结构元素小的洞
fc=imclose(f,se);%直接闭运算
subplot(222),imshow(fc);
title(‘直接闭运算‘);

foc=imclose(fo,se);%先开后闭运算
subplot(223),imshow(foc);
title(‘先开后闭运算‘);

fco=imopen(fc,se);%先闭后开运算
subplot(224),imshow(fco);
title(‘先闭后开运算‘);
 84%开闭运算结果如下：


%先膨胀再腐蚀
fse=imdilate(f,se);%膨胀

%gcf为得到当前图像的句柄，当前图像是指例如PLOT,TITLE,SURF等
%get函数为得到物体的属性，get(0,‘screensize‘)为返回所有物体screensize属性值
%set函数为设置物体的属性
figure,set(gcf,‘outerposition‘,get(0,‘screensize‘));%具体目的是设置当前窗口的大小
subplot(211),imshow(fse);
title(‘使用disk(5)先膨胀后的图像‘);

fes=imerode(fse,se);
subplot(212),imshow(fes);
title(‘使用disk(5)先膨胀再腐蚀后的图像‘);
 99%先膨胀后腐蚀图像如下：

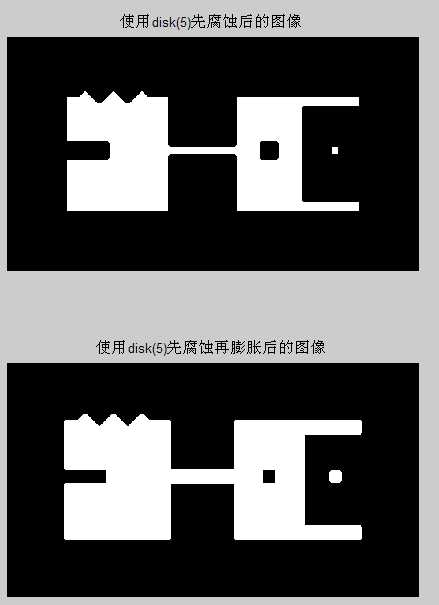
%先腐蚀再膨胀
fse=imerode(f,se);
figure,set(gcf,‘outerposition‘,get(0,‘screensize‘))
subplot(211),imshow(fse);
title(‘使用disk(5)先腐蚀后的图像‘);

fes=imdilate(fse,se);
subplot(212),imshow(fes);
title(‘使用disk(5)先腐蚀再膨胀后的图像‘);
110%先腐蚀后膨胀的图像如下：


%% imopen imclose在指纹上的应用
clc
clear
f=imread(‘.\images\dipum_images_ch09\Fig0911(a)(noisy-fingerprint).tif‘);
se=strel(‘square‘,3);%边长为3的方形结构元素
subplot(121),imshow(f);
title(‘指纹原始图像‘);

A=imerode(f,se);%腐蚀
subplot(122),imshow(A);
title(‘腐蚀后的指纹原始图像‘);
123%指纹原始图像和腐蚀后的图像结果如下：


fo=imopen(f,se);
figure,subplot(221),imshow(fo);
title(‘使用square(3)开操作后的图像‘);

fc=imclose(f,se);
subplot(222),imshow(fc);
title(‘使用square闭操作后的图像‘);

foc=imclose(fo,se);
subplot(223),imshow(foc);
title(‘使用square(3)先开后闭操作后的图像‘)

fco=imopen(fc,se);
subplot(224),imshow(fco);
title(‘使用square(3)先闭后开操作后的图像‘);
140%指纹图像开闭操作过程结果如下：

%% bwhitmiss击中或击不中变换
clc
clear
f=imread(‘.\images\dipum_images_ch09\Fig0913(a)(small-squares).tif‘);
imshow(f);
title(‘击中或不击中原始图像‘);
148%击中或不击中原始图像显示结果如下：


B1=strel([0 0 0;0 1 1;0 1 0]);%击中：要求击中所有1的位置
B2=strel([1 1 1;1 0 0;1 0 0]);%击不中，要求击不中所有1的位置
B3=strel([0 1 0;1 1 1;0 1 0]);%击中
B4=strel([1 0 1;0 0 0;0 0 0]);%击不中
B5=strel([0 0 0;0 1 0;0 0 0]);%击中
B6=strel([1 1 1;1 0 0;1 0 0]);%击不中

g=imerode(f,B1)&imerode(~f,B2)%利用定义来实现击中或击不中
figure,subplot(221),imshow(g);
title(‘定义实现组1击中击不中图像‘);

g1=bwhitmiss(f,B1,B2);
subplot(222),imshow(g1);
title(‘结构数组1击中击不中后的图像‘);

g2=bwhitmiss(f,B3,B4);
subplot(223),imshow(g2);
title(‘结构数组2击中击不中的图像‘);

g3=bwhitmiss(f,B5,B6);
subplot(224),imshow(g3);
title(‘结构数组3击中击不中的图像‘);
172%击中击不中变换后图像如下：

%%makelut
clc
clear

f=inline(‘sum(x(:))>=3‘);%inline是用来定义局部函数的
lut2=makelut(f,2)%为函数f构造一个接收2*2矩阵的查找表
lut3=makelut(f,3)

%% Conway生命游戏
clc
clear
lut=makelut(@conwaylaws,3);
bw1=  [0     0     0     0     0     0     0     0     0     0
       0     0     0     0     0     0     0     0     0     0
       0     0     0     1     0     0     1     0     0     0
       0     0     0     1     1     1     1     0     0     0
       0     0     1     0     0     0     0     1     0     0
       0     0     1     0     1     1     0     1     0     0
       0     0     1     0     0     0     0     1     0     0
       0     0     0     1     1     1     1     0     0     0
       0     0     0     0     0     0     0     0     0     0
       0     0     0     0     0     0     0     0     0     0  ];
subplot(221),imshow(bw1,‘InitialMagnification‘,‘fit‘);
title(‘Generation 1‘);

bw2=applylut(bw1,lut);
subplot(222),imshow(bw2,‘InitialMagnification‘,‘fit‘),
title(‘Generation 2‘);

bw3=applylut(bw2,lut);
subplot(223),imshow(bw3,‘InitialMagnification‘,‘fit‘);
title(‘Generation 3‘);

temp=bw1;
for i=2:100
    bw100=applylut(temp,lut);
    temp=bw100;
end
subplot(224),imshow(bw100,‘InitialMagnification‘,‘fit‘)
title(‘Generation 100‘);
214%显示Generation结果如下：


%% getsequence
clc
clear
se=strel(‘diamond‘,5)
decomp=getsequence(se)%getsequence函数为得到分解的strel序列
decomp(1)
decomp(2)

%% endpoints
clc
clear

f1=imread(‘.\images\dipum_images_ch09\Fig0914(a)(bone-skel).tif‘);
subplot(121),imshow(f1);
title(‘原始形态骨架图像‘);

g1=endpoints(f1);
%set(gcf,‘outerposition‘,get(0,‘screensize‘));%运行完后自动生成最大的窗口
subplot(122),imshow(g1);
title(‘骨架图像的端点图像‘);
%骨架头像端点检测头像如下：


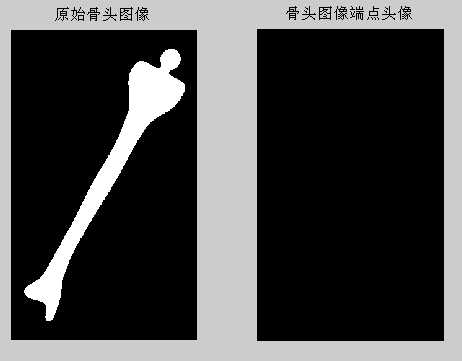
f2=imread(‘.\images\dipum_images_ch09\Fig0916(a)(bone).tif‘);
figure,subplot(121),imshow(f2);
title(‘原始骨头图像‘);

g2=endpoints(f2);
subplot(122),imshow(g2);
title(‘骨头图像端点头像‘);%结果是没有端点
245%骨头头像端点检测图像如下：

%% bwmorph组合常见形态学之细化
clc
clear
f=imread(‘.\images\dipum_images_ch09\Fig0911(a)(noisy-fingerprint).tif‘);
subplot(221),imshow(f);
title(‘指纹图像细化原图‘);

g1=bwmorph(f,‘thin‘,1);
subplot(222),imshow(g1);
title(‘指纹图像细化原图‘);

g2=bwmorph(f,‘thin‘,2);
subplot(223),imshow(g2);
title(‘指纹图像细化原图‘);

g3=bwmorph(f,‘thin‘,Inf);
subplot(224),imshow(g3);
title(‘指纹图像细化原图‘);
265%指纹图像细化过程显示如下：

%% bwmorph组合常见形态学之骨骼化
clc
clear
f=imread(‘.\images\dipum_images_ch09\Fig0911(a)(noisy-fingerprint).tif‘);
subplot(131),imshow(f);
title(‘指纹图像骨骼化原图‘);

fs=bwmorph(f,‘skel‘,Inf);
subplot(132),imshow(fs);
title(‘指纹图像骨骼化‘);

for k=1:5
    fs=fs&~endpoints(fs);
end
subplot(133),imshow(fs);
title(‘指纹图像修剪后骨骼话‘);
283%指纹图像骨骼化过程显示：


%% 使用函数bwlabel标注连通分量
clc
clear
f=imread(‘.\images\dipum_images_ch09\Fig0917(a)(ten-objects).tif‘);
imshow(f),title(‘标注连通分量原始图像‘);
290%其结果显示如下：


[L,n]=bwlabel(f);%L为标记矩阵，n为找到连接分量的总数
[r,c]=find(L==3);%返回第3个对象所有像素的行索引和列索引

rbar=mean(r);
cbar=mean(c);

figure,imshow(f)
hold on%保持当前图像使其不被刷新
for k=1:n
    [r,c]=find(L==k);
    rbar=mean(r);
    cbar=mean(c);
    plot(cbar,rbar,‘Marker‘,‘o‘,‘MarkerEdgeColor‘,‘k‘,...
         ‘MarkerFaceColor‘,‘k‘,‘MarkerSize‘,10);%这个plot函数用法不是很熟悉
    plot(cbar,rbar,‘Marker‘,‘*‘,‘MarkerFaceColor‘,‘w‘);%其中的marker为标记
end
title(‘标记所有对象质心后的图像‘);

%% 由重构做开运算
clc
clear
f=imread(‘.\images\dipum_images_ch09\Fig0922(a)(book-text).tif‘);
subplot(321),imshow(f);
title(‘重构原始图像‘);

fe=imerode(f,ones(51,1));%竖线腐蚀
subplot(322),imshow(fe);
title(‘使用竖线腐蚀后的结果‘);

fo=imopen(f,ones(51,1));%竖线做开运算
subplot(323),imshow(fo);
title(‘使用竖线做开运算结果‘);

fobr=imreconstruct(fe,f);%fe做标记
subplot(324),imshow(fobr);
title(‘使用竖线做重构开运算‘);

ff=imfill(f,‘holes‘);%对f进行孔洞填充
subplot(325),imshow(ff);
title(‘对f填充孔洞后的图像‘);

fc=imclearborder(f,8);%清除边界，2维8邻接
subplot(326),imshow(fc);
title(‘对f清除边界后的图像‘);
336%图像重构过程显示如下：

%% 使用顶帽变换和底帽变换
clc
clear
f=imread(‘.\images\dipum_images_ch09\Fig0926(a)(rice).tif‘);
subplot(221),imshow(f);
title(‘顶帽底帽变换原始图像‘);

se=strel(‘disk‘,10);%产生结构元素
%顶帽变换是指原始图像减去其开运算的图像
%而开运算可用于补偿不均匀的背景亮度，所以用一个大的结构元素做开运算后
%然后用原图像减去这个开运算，就得到了背景均衡的图像，这也叫做是图像的顶帽运算
f1=imtophat(f,se);%使用顶帽变换
subplot(222),imshow(f1);
title(‘使用顶帽变换后的图像‘);

%底帽变换是原始图像减去其闭运算后的图像
f2=imbothat(imcomplement(f),se);%使用底帽变换，为什么原图像要求补呢？
%f2=imbothat(f,se);%使用底帽变换
subplot(223),imshow(f2);
title(‘使用底帽变换后的图像‘);

%顶帽变换和底帽变换联合起来用，用于增加对比度
f3=imsubtract(imadd(f,imtophat(f,se)),imbothat(f,se));%里面参数好像不合理？
subplot(224),imshow(f3);
title(‘使用顶帽底帽联合变换后图像‘);
363%顶帽底帽变换过程图像如下：


%%使用开运算和闭运算做形态学平滑
%由于开运算可以除去比结构元素更小的明亮细节，闭运算可以除去比结构元素更小的暗色细节
%所以它们经常组合起来一起进行平滑图像并去除噪声
clc
clear
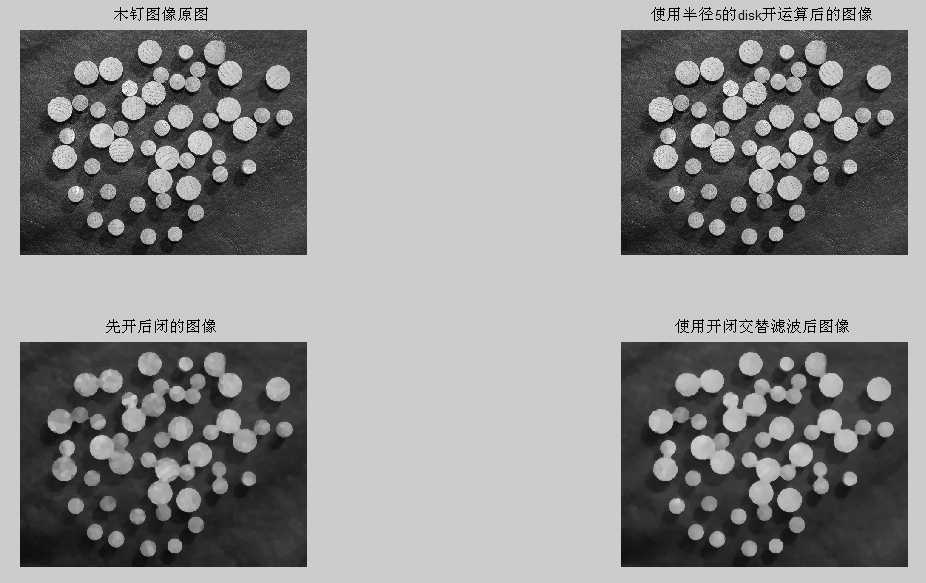
f=imread(‘.\images\dipum_images_ch09\Fig0925(a)(dowels).tif‘);
subplot(221),imshow(f);
title(‘木钉图像原图‘);

se=strel(‘disk‘,5);%disk其实就是一个八边形
fo=imopen(f,se);%经过开运算
subplot(222),imshow(f);
title(‘使用半径5的disk开运算后的图像‘);

foc=imclose(fo,se);
subplot(223),imshow(foc);
title(‘先开后闭的图像‘);

fasf=f;
for i=2:5
    se=strel(‘disk‘,i);
    fasf=imclose(imopen(fasf,se),se);
end
subplot(224),imshow(fasf);
title(‘使用开闭交替滤波后图像‘);
390%使用开运算和闭运算做形态学平滑结果如下：


%% 颗粒分析
clc
clear
f=imread(‘.\images\dipum_images_ch09\Fig0925(a)(dowels).tif‘);

sumpixels=zeros(1,36);
for k=0:35
    se=strel(‘disk‘,k);
    fo=imopen(f,se);
    sumpixels(k+1)=sum(fo(:));
end

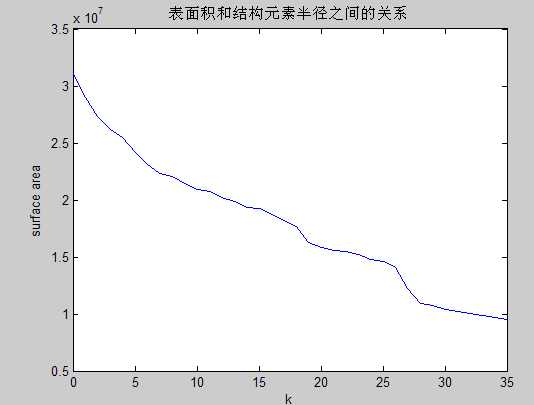
%可以看到，连续开运算之间的表面积会减少
plot(0:35,sumpixels),xlabel(‘k‘),ylabel(‘surface area‘);
title(‘表面积和结构元素半径之间的关系‘);
407%其运算结果如下：   


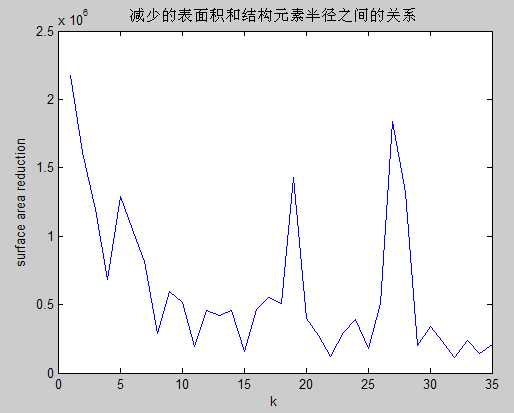
figure,plot(-diff(sumpixels));%diff()函数为差分或者近似倒数，即相邻2个之间的差值
xlabel(‘k‘),ylabel(‘surface area reduction‘);
title(‘减少的表面积和结构元素半径之间的关系‘);
412%其运算结果如下：


%% 使用重构删除复杂图像的背景
clc
clear
f=imread(‘.\images\dipum_images_ch09\Fig0930(a)(calculator).tif‘);
subplot(221),imshow(f);
title(‘灰度级重构原图像‘);

f_obr=imreconstruct(imerode(f,ones(1,71)),f);
subplot(222),imshow(f_obr);
title(‘经开运算重构图‘);

f_o=imopen(f,ones(1,71));
subplot(223),imshow(f_o);
title(‘经开运算后图‘);

f_thr=imsubtract(f,f_obr);
subplot(224),imshow(f_thr);
title(‘顶帽运算重构图‘)
432%使用重构删除复杂图像的背景1:


f_th=imsubtract(f,f_o)
figure,subplot(221),imshow(f_th);
title(‘经顶帽运算图‘);

g_obr=imreconstruct(imerode(f_thr,ones(1,11)),f_thr);
subplot(222),imshow(g_obr);
title(‘用水平线对f_thr经开运算后重构图‘);

g_obrd=imdilate(g_obr,ones(1,2));
subplot(223),imshow(g_obrd);
title(‘使用水平线对上图进行膨胀‘);

f2=imreconstruct(min(g_obrd,f_thr),f_thr);
subplot(224),imshow(f2);
title(‘最后的重构结果‘);
449%使用重构删除复杂图像的背景2: