·专题」线段树

时间：2014-07-20 09:06:47 阅读：509 评论：0 收藏：0 [点我收藏+]

PKU暑期培训第一天，这次培训人很多，但是感觉打酱油的也不少，不知道大牛有多少。

第一天都是讲线段树的，课件的话和往常一样，没什么变化。

具体的话，讲了线段树和树状数组。线段树的话讲了单点更新，成段更新，扫描线已经离散化。

然后随便提了提树状数组。估计明天再讲一点点，然后接着是讲并查集，多串匹配什么的。

线段树的题目我做得很少，以前看过HH大神的模板，想模仿来着，其实也没什么理解。

重新理解一下线段树吧。

线段树的用途，主要是维护区间问题，比如区间的单点更新操作，成段更新，扫描线等等。
当然还有一个编程复杂度更低的树状数组BIT，主要用于维护区间。

线段树是一棵二叉树
存储的形式可以用完全二叉树来存储（但是线段树并不是一棵完全二叉树，而是一颗真二叉树）
存储的话可以不需要使用指针，而通过下标计算来确定位置。(如果使用完全二叉树的形式存储，需要开辟4n的空间)
然后是域，根据不同的问题，有特定的阈值，比如最大值最小值，区间和等等。

学习大牛的模板，一般好像没有特意去封一个struct来存放各种阈值，而是都是用全局的一位数组来存，我暂且也这样搞吧。



然后我明白要从这里开始刷题生涯
http://blog.csdn.net/shiqi_614/article/details/8228102

HH大神的模板，大概是这样的
首先用了宏定义 lson rson 我自己再加上了mid等宏定义

线段树最强大的功能是支持区间修改，求和等操作。
主要的题目有 单点修改(可以用树状数组)，区间修改，扫描线，区间合并
然后需要用到的可以有离散化
然后还有二维的线段树(树套树)

然后开始我的刷题生涯，记录在这个帖子里，怒刷线段树

一、单点更新

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
#define mid(l,r) (l + r) >> 1
#define inf 0x3f3f3f3f
#define maxn 55555 
int N,T,a,b,cas=1;
char op[10];

struct seg_tree
{
    int SUM[maxn << 2];                //线段树的域，这里用来存放某个区间的和 
    
    void PushUp(int rt)                //向上更新 
    {
        SUM[rt] = SUM[rt<<1] + SUM[rt<<1|1];
    }
    void build(int l,int r,int rt)    //建树 
    {
        if(l == r)
        {
            scanf("%d",&SUM[rt]);
            return;
        }
        int m = mid(l,r);
        build(lson);
        build(rson);
        PushUp(rt);
    }
    
    void update(int pos,int add,int l,int r,int rt)    //更新，这里是单点更新 
    {
        if(l == r)
        {
            SUM[rt] += add;
            return;
        }
        int m = mid(l,r);
        if(pos <= m)    update(pos,add,lson);
        else            update(pos,add,rson);
        PushUp(rt);
    }
    
    int query(int L,int R,int l,int r,int rt)        //询问操作 
    {
        if(L <= l && r <= R)    return SUM[rt];
        int m = mid(l,r);
        int ret = 0;
        if(L <= m)        ret += query(L,R,lson);
        if(R >     m)        ret += query(L,R,rson);
        return ret;    
    }
}st;

int main()
{
    scanf("%d",&T);
    while(T--)
    {
        printf("Case %d:\n",cas++);
        scanf("%d",&N);
        st.build(1,N,1);
        while(true)
        {
            scanf("%s",op);
            if(op[0] == ‘E‘)    break;
            scanf("%d %d",&a,&b);
            if(op[0] == ‘A‘)            st.update(a,b,1,N,1);
            else if(op[0] == ‘S‘)        st.update(a,-b,1,N,1);
            else            printf("%d\n",st.query(a,b,1,N,1));
        }
    }
    
    return 0;
}

模板君

1. HDU 1166 敌兵布阵

题意: 中文题目，就是给出一个区间，然后需要对这个区间的某个值进行修改(add or sub)，或者求区间的和
分析: 线段树的模板题目，也可以用树状数组，这里学习的是HH大神的模板风格。
注释: 线段树入门的第一题，当时写出来还是磕磕碰碰的，但是要坚定信念！！！！

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
#define mid(l,r) (l + r) >> 1
#define inf 0x3f3f3f3f
#define maxn 55555 
int N,T,a,b,cas=1;
char op[10];

struct seg_tree
{
    int SUM[maxn << 2];                //线段树的域，这里用来存放某个区间的和 
    
    void PushUp(int rt)                //向上更新 
    {
        SUM[rt] = SUM[rt<<1] + SUM[rt<<1|1];
    }
    void build(int l,int r,int rt)    //建树 
    {
        if(l == r)
        {
            scanf("%d",&SUM[rt]);
            return;
        }
        int m = mid(l,r);
        build(lson);
        build(rson);
        PushUp(rt);
    }
    
    void update(int pos,int add,int l,int r,int rt)    //更新，这里是单点更新 
    {
        if(l == r)
        {
            SUM[rt] += add;
            return;
        }
        int m = mid(l,r);
        if(pos <= m)    update(pos,add,lson);
        else            update(pos,add,rson);
        PushUp(rt);
    }
    
    int query(int L,int R,int l,int r,int rt)        //询问操作 
    {
        if(L <= l && r <= R)    return SUM[rt];
        int m = mid(l,r);
        int ret = 0;
        if(L <= m)        ret += query(L,R,lson);
        if(R >  m)        ret += query(L,R,rson);
        return ret;    
    }
}st;

int main()
{
    scanf("%d",&T);
    while(T--)
    {
        printf("Case %d:\n",cas++);
        scanf("%d",&N);
        st.build(1,N,1);
        while(true)
        {
            scanf("%s",op);
            if(op[0] == ‘E‘)    break;
            scanf("%d %d",&a,&b);
            if(op[0] == ‘A‘)            st.update(a,b,1,N,1);
            else if(op[0] == ‘S‘)        st.update(a,-b,1,N,1);
            else            printf("%d\n",st.query(a,b,1,N,1));
        }
    }
    
    return 0;
}

代码君

2. POJ 3264 Balanced Lineup

题意: 给出一个区间，求这个区间的最大值和最小值的差。
分析: 熟悉模板用，然后这道题目没有更新操作(update)，只有找最大值最小值。
注释:

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
#define mid(r,l) (r + l) >> 1
#define maxn 200000
#define inf 0x3f3f3f3f
int N,Q;

struct seg_tree
{
    //线段树的两个阈 
    int MAX[maxn << 2];
    int MIN[maxn << 2];
    //向上更新
    void PushUp(int rt)
    {
        MIN[rt] = min(MIN[rt<<1], MIN[rt<<1|1]);
        MAX[rt] = max(MAX[rt<<1], MAX[rt<<1|1]);
    } 
    //建树，直接插入元素，并向上更新 
    void build(int l,int r,int rt)
    {
        if(l == r)
        {
            scanf("%d",&MAX[rt]);
            MIN[rt] = MAX[rt];
            return;
        }
        int m = mid(l,r);
        build(lson);
        build(rson);
        //插入值并向上更新(向父亲节点) 
        PushUp(rt);
    }
    //这道题目没有单点更新或者说成段更新操作，没有update函数
    int isMax(int L,int R,int l,int r,int rt)
    {
        if(L <= l && r <= R)    return MAX[rt];
        int m = mid(l,r);
        int ret = -inf;
        if(L <= m)    ret = max(ret,isMax(L,R,lson));
        if(R >  m)    ret = max(ret,isMax(L,R,rson));
        return ret;
    } 
    int isMin(int L,int R,int l,int r,int rt)
    {
        if(L <= l && r <= R)    return MIN[rt];
        int m = mid(l,r);
        int ret = inf;
        if(L <= m)    ret = min(ret,isMin(L,R,lson));
        if(R >  m)    ret = min(ret,isMin(L,R,rson));
        return ret;
    }
}st;


int main()
{
    while(~scanf("%d %d",&N,&Q))
    {
        st.build(1,N,1);
        while(Q--)
        {
            int a, b;
            scanf("%d %d",&a,&b);
            printf("%d\n",st.isMax(a,b,1,N,1) - st.isMin(a,b,1,N,1));
        }
    }
    return 0;
}

代码君

3. POJ 2182 Lost Cows

4. HDU 1754 I Hate It

题意: 需要对区间单点进行修改，然后是求区间的最值
分析: 线段树入门，熟悉模板
注释:

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define lson l, m, rt << 1
#define rson m + 1, r , rt << 1 | 1
#define inf 0x3f3f3f3f
#define mid(l,r) (l + r) >> 1
#define maxn 200000
int N,Q,a,b;
char op[10];

struct seg_tree
{
    int MAX[maxn << 2];
    
    void PushUp(int rt)
    {
        MAX[rt] = max(MAX[rt<<1],MAX[rt<<1|1]);
    }
    
    void build(int l,int r,int rt)
    {
        if(l == r)
        {
            scanf("%d",&MAX[rt]);
            return;
        }
        int m = mid(l,r);
        build(lson);
        build(rson);
        PushUp(rt);
    }
    
    void update(int pos,int sco,int l,int r,int rt)
    {
        if(l == r)
        {
            MAX[rt] = sco;
            return;
        }
        int m = mid(l,r);
        if(pos <= m)    update(pos,sco,lson);
        else            update(pos,sco,rson);
        PushUp(rt);
    }
    
    int query(int L,int R,int l,int r,int rt)
    {
        if(L <= l && r <= R)    return MAX[rt];
        int m = mid(l,r);
        int ret = -inf;
        if(L <= m)    ret = max(ret,query(L,R,lson));
        if(R >  m)    ret = max(ret,query(L,R,rson));
        return ret;
    }
}st;



int main()
{
    while(~scanf("%d %d",&N,&Q))
    {
        st.build(1,N,1);
        while(Q--)
        {
            scanf("%s %d %d",&op,&a,&b);
            if(op[0] == ‘Q‘)    printf("%d\n",st.query(a,b,1,N,1));
            else            st.update(a,b,1,N,1);
        }
    }
    return 0;
}

代码君

。。。。。。。待续

二、成段更新

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define lson l, m, rt << 1
#define rson m + 1, r ,rt << 1 | 1
#define mid(l,r) (l + r) >> 1
#define inf 0x3f3f3f3f
#define LL long long
#define maxn 111111
int N,Q,a,b,c;
char op[2];

struct seg_tree
{
    LL lazy[maxn << 2];    //inc标记累加标记,懒惰标记 
    LL sum[maxn << 2];    //区间求和用 

    void PushUp(int rt)
    {
        sum[rt] = sum[rt<<1] + sum[rt<<1|1];
    }

    void PushDown(int rt,int m)        //向下更新 
    {
        if(lazy[rt])
        {
            lazy[rt<<1]   += lazy[rt];
            lazy[rt<<1|1] += lazy[rt];
            sum[rt<<1]   += lazy[rt] * (m - (m >> 1));
            sum[rt<<1|1] += lazy[rt] * (m >> 1);
            lazy[rt] = 0;
        }
    }

    void build(int l,int r,int rt)
    {
        lazy[rt] = 0;
        if(l == r)
        {
            scanf("%lld",&sum[rt]);
            return;
        }
        int m = mid(l,r);
        build(lson);
        build(rson);
        PushUp(rt);
    }

    void update(int L,int R,int c,int l,int r,int rt)
    {
        if(L <= l && r <= R)
        {
            lazy[rt] += c;
            sum[rt] += (LL)c * (r - l + 1);
            return;
        }
        PushDown(rt, r - l + 1);
        int m = mid(l,r);
        if(L <= m)    update(L,R,c,lson);
        if(m <  R)    update(L,R,c,rson);
        PushUp(rt);
    }

    LL query(int L,int R,int l,int r,int rt)
    {
        if(L <= l && r <= R)    return sum[rt];

        PushDown(rt,r - l + 1);
        int m = mid(l,r);
        LL ret = 0;
        if(L <= m)    ret += query(L,R,lson);
        if(m <  R)    ret += query(L,R,rson);
        return ret;
    }
}st;

int main()
{
    scanf("%d %d",&N,&Q);
    st.build(1,N,1);
    while(Q--)
    {
        scanf("%s",op);
        if(op[0] == ‘Q‘)
        {
            scanf("%d %d",&a,&b);
            printf("%lld\n",st.query(a,b,1,N,1));
        }
        else
        {
            scanf("%d %d %d",&a,&b,&c);
            st.update(a,b,c,1,N,1);
        }
    }
    return 0;
}

模板君

1. POJ 3468 A Simple Problem with Integers

题意: 给定Q(1 ≤ Q≤ 100,000)个数A1,A2… AQ,，以及可能多次进行的两个操作:
　　1)对某个区间Ai … Aj的每个数都加n(n可变）
　　2) 求某个区间Ai … Aj的数的和
分析: 套用成段更新模板，，主要理解懒惰标记
注释:

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define lson l, m, rt << 1
#define rson m + 1, r ,rt << 1 | 1
#define mid(l,r) (l + r) >> 1
#define inf 0x3f3f3f3f
#define LL long long
#define maxn 111111
int N,Q,a,b,c;
char op[2];

struct seg_tree
{
    LL lazy[maxn << 2];    //inc标记累加标记
    LL sum[maxn << 2];

    void PushUp(int rt)
    {
        sum[rt] = sum[rt<<1] + sum[rt<<1|1];
    }

    void PushDown(int rt,int m)
    {
        if(lazy[rt])
        {
            lazy[rt<<1]   += lazy[rt];
            lazy[rt<<1|1] += lazy[rt];
            sum[rt<<1]   += lazy[rt] * (m - (m >> 1));
            sum[rt<<1|1] += lazy[rt] * (m >> 1);
            lazy[rt] = 0;
        }
    }

    void build(int l,int r,int rt)
    {
        lazy[rt] = 0;
        if(l == r)
        {
            scanf("%lld",&sum[rt]);
            return;
        }
        int m = mid(l,r);
        build(lson);
        build(rson);
        PushUp(rt);
    }

    void update(int L,int R,int c,int l,int r,int rt)
    {
        if(L <= l && r <= R)
        {
            lazy[rt] += c;
            sum[rt] += (LL)c * (r - l + 1);
            return;
        }
        PushDown(rt, r - l + 1);
        int m = mid(l,r);
        if(L <= m)    update(L,R,c,lson);
        if(m <  R)    update(L,R,c,rson);
        PushUp(rt);
    }

    LL query(int L,int R,int l,int r,int rt)
    {
        if(L <= l && r <= R)    return sum[rt];

        PushDown(rt,r - l + 1);
        int m = mid(l,r);
        LL ret = 0;
        if(L <= m)    ret += query(L,R,lson);
        if(m <  R)    ret += query(L,R,rson);
        return ret;
    }
}st;

int main()
{
    scanf("%d %d",&N,&Q);
    st.build(1,N,1);
    while(Q--)
    {
        scanf("%s",op);
        if(op[0] == ‘Q‘)
        {
            scanf("%d %d",&a,&b);
            printf("%lld\n",st.query(a,b,1,N,1));
        }
        else
        {
            scanf("%d %d %d",&a,&b,&c);
            st.update(a,b,c,1,N,1);
        }
    }
    return 0;
}

代码君

2. HDU 1698 Just a hook

题意: 
分析: 套用成段更新模板，，主要理解懒惰标记
注释:

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
#define mid(l,r) (l + r) >> 1
#define inf 0x3f3f3f3f
#define maxn 111111
int h, w, n, m, t;

struct seg_tree
{
    int lazy[maxn << 2];
    int sum[maxn << 2];
    
    void PushUp(int rt)
    {
        sum[rt] = sum[rt<<1] + sum[rt<<1|1];
    }
    
    void PushDown(int rt,int m)
    {
        if(lazy[rt])
        {
            lazy[rt<<1]  = lazy[rt<<1|1] = lazy[rt];
            sum[rt<<1]   = lazy[rt] * (m  - (m >> 1));
            sum[rt<<1|1] = lazy[rt] * (m >> 1);
            lazy[rt] = 0;
        }
    }
    
    void build(int l,int r,int rt)
    {
        lazy[rt] = 0;
        sum[rt] = 1;
        if(l == r)    return;
        int m = mid(l,r);
        build(lson);
        build(rson);
        PushUp(rt);
    }
    
    void update(int L,int R,int c,int l,int r,int rt)
    {
        //对L-R这个区间进行成段修改
        if(L <= l && r <= R)
        {
            lazy[rt] = c;
            sum[rt] = c*(r - l + 1);
            return;
        } 
        PushDown(rt,r - l + 1);
        int m = mid(l,r);
        if(L <= m)    update(L,R,c,lson);
        if(R >  m)    update(L,R,c,rson);
        PushUp(rt);
    }
}st;

int main()
{
    scanf("%d",&t);
    int cas = 1;
    while(t--)
    {
        scanf("%d%d",&n,&m);
        st.build(1,n,1);
        while(m--)
        {
            int a, b, c;
            scanf("%d %d %d",&a,&b,&c);
            st.update(a,b,c,1,n,1);
        }
        printf("Case %d: The total value of the hook is %d.\n",cas++ , st.sum[1]);
    }
    return 0;
}

代码君

三、扫描线

扫描线真的是第一次做，一开始理解起来很吃力。
后来看别人博客明白了。
就是用的一条线从某一侧从某个方向扫到另外一个方向
这类题目需要将一些操作排序,然后从左到右用一根扫描线(当然是在我们脑子里)扫过去
最典型的就是矩形面积并,周长并等题

1. POJ 1151 Atlantis(扫描线+离散化 / 面积并)

这道题是我的第一道扫描线的题目，而且这道题目还需要进行离散化，
刚开始做这道题目的时候感觉很困难。
最后还是想明白了。


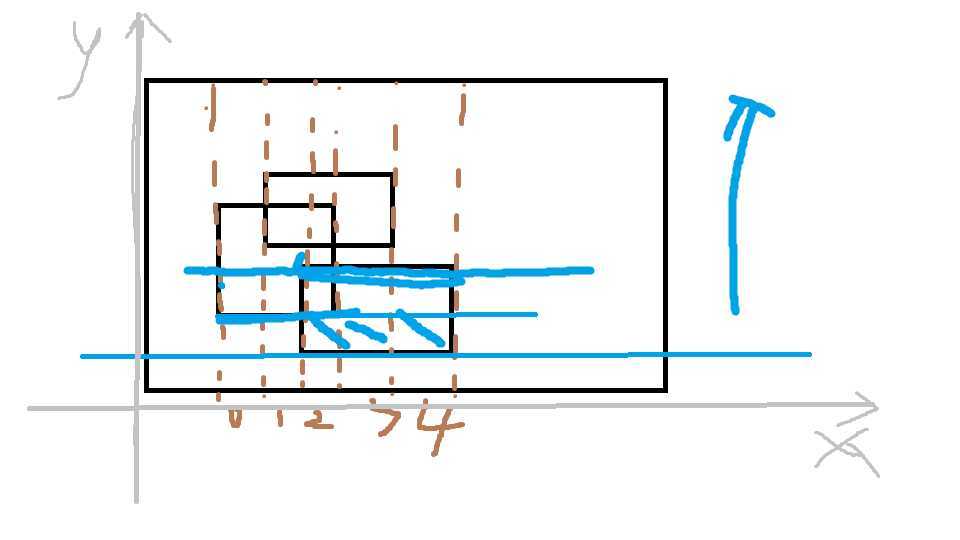
可以把x方向进行离散化(y方向也是一个意思)
然后对y方向上的矩形的开始位置进行排序，从下往上扫描
长=线段树被覆盖的总长度，宽=当前线段树扫描到的位置-前一个位置(Line[i+1].y - Line[i].y)
那么面积并就是从下往上以此扫描再一次累加。(累加的同时更新整个区间，也就是求新的长)

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
#define mid(l,r) (l + r ) >> 1
#define CLR(a,b) memset(a,b,sizeof(a))
#define maxn 222

int    cov[maxn << 2];
double sum[maxn << 2];
double coo[maxn];
int n, cas = 1;

struct Sn
{
    double x1, x2, y;
    int fl;
    Sn() {};
    Sn(double a,double b,double c,int d) : x1(a), x2(b), y(c), fl(d) {};
    bool operator<(const Sn &t) const
    {
        return y < t.y;
    }
}Line[maxn];

void PushUp(int l,int r,int rt)
{
    if(cov[rt])    sum[rt] = coo[r+1] - coo[l];
    else if(l == r)    sum[rt] = 0;
    else    sum[rt] = sum[rt<<1] + sum[rt<<1|1];
}

void update(int L,int R,int c,int l,int r,int rt)
{
    if(L <= l && r <= R)
    {
        cov[rt] += c;
        PushUp(l,r,rt);
        return;
    }
    int m = mid(l,r);
    if(L <= m)    update(L,R,c,lson);
    if(R >  m)    update(L,R,c,rson);
    PushUp(l,r,rt);
}

int BS(int l,int r,double key)
{
    while(l <= r)
    {
        int m = mid(l,r);
        if(coo[m] == key)    return m;
        if(coo[m] <  key)    l = m + 1;
        else                r = m - 1;
    }
    return -1;
}

int main()
{
    while(~scanf("%d",&n) && n)
    {
        int ct = 0;
        while(n--)
        {
            double a,b,c,d;
            scanf("%lf%lf%lf%lf",&a,&b,&c,&d);
            coo[ct] = a;
            Line[ct++] = Sn(a,c,b,1);    //左边
            coo[ct] = c; 
            Line[ct++] = Sn(a,c,d,-1);    //右边 
        }
        sort(coo,coo+ct);
        sort(Line,Line+ct);
        int k = 1;
        for(int i=1;i<ct;i++)
        {
            if(coo[i] != coo[i-1])    coo[k++] = coo[i];
        }
        CLR(cov,0);CLR(sum,0);
        double ret = 0;
        for(int i=0;i<ct-1;i++)
        {
            int l = BS(0,k-1,Line[i].x1);
            int r = BS(0,k-1,Line[i].x2) - 1;    //这里要-1 
            if(l <= r)    update(l,r,Line[i].fl,0,k-1,1);//全段更新 区间为0~k-1，根为1 
            ret += sum[1] * (Line[i+1].y - Line[i].y);//长*宽 
        }
        printf("Test case #%d\nTotal explored area: %.2f\n\n",cas++ ,ret);
    }
    return 0;
}

代码君

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
#define mid(l,r)    (l + r) >> 1
#define inf 0x3f3f3f3f
#define maxn 111
#define clr(a,b) memset(a,b,sizeof(a))

struct Line //纵向线的结构体
{
    double x, y1, y2;   //横坐标，两个纵坐标
    int fl;             //边标记，标记是左边还是右边(+1,-1)
    Line()  {};         //构造函数
    Line(double a,double b,double c,int d) : y1(a), y2(b), x(c), fl(d) {};  //构造函数
    bool operator<(const Line &m) const         //重载<以便排序使用
    {
        return x < m.x;
    }
};


Line L[maxn<<1];        //纵向线总数最多为maxn<<1
int cov[maxn<<3];       //cov数组记录本区间被覆盖的次数
double sum[maxn<<3];    //记录区间的和，纵向上的区间，
double coo[maxn<<3];    //记录纵向上的左边，并且纵向需要进行离散化

void PushUp(int l,int r,int rt)
{
    if(cov[rt]) sum[rt] = coo[r+1] - coo[l];        //如果该区间被覆盖，更新纵向和(也就是矩形的宽)
    else if(l == r)   sum[rt] = 0;                  //端点重合则没有长度
    else sum[rt] = sum[rt<<1] + sum[rt<<1|1];       //向上更新
}

void Update(int L,int R,int c,int l,int r,int rt)   //区间更新
{
    if(L <= l && r <= R)
    {
        cov[rt] += c;
        PushUp(l,r,rt);
        return;
    }
    int m = mid(l,r);
    if(L <= m)  Update(L,R,c,lson);
    if(R >  m)  Update(L,R,c,rson);
    PushUp(l,r,rt);
}

int BS(int l,int r,double key)          //二分查找
{
    while(l <= r)
    {
        int m = mid(l,r);
        if(coo[m] == key) return m;
        else if(coo[m] > key) r = m - 1;
        else    l = m + 1;
    }
    return -1;
}

int n,cas = 1;
double x1,y1,x2,y2;
int main()
{
    while(~scanf("%d",&n) && n)
    {
        int cnt = 0;
        double ret = 0;
        for(int i=0;i<n;i++)
        {
            scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
            L[cnt] = Line(y1,y2,x1,1);      //记录纵向线
            coo[cnt++] = y1;                //记录纵坐标
            L[cnt] = Line(y1,y2,x2,-1);
            coo[cnt++] = y2;
        }
        sort(L,L+cnt);
        sort(coo,coo+cnt);
        int t = 1;
        for(int i=1;i<cnt;i++)              //纵轴进行离散化，离散化后仅有t个y坐标
        {
            if(coo[i] != coo[i-1])  coo[t++] = coo[i];
        }

        clr(cov,0),clr(sum,0);

        for(int i=0;i<cnt-1;i++)
        {
            int l = BS(0,t-1,L[i].y1);
            int r = BS(0,t-1,L[i].y2) - 1;
            if(l <= r)  Update(l,r,L[i].fl,0,t-1,1);
            ret += sum[1] * (L[i+1].x - L[i].x);
        }
        printf("Test case #%d\nTotal explored area: %.2f\n\n",cas++,ret);
    }

    return 0;
}

代码君(纵向离散)

2. POJ 1177 Picture(扫描线 / 周长并)

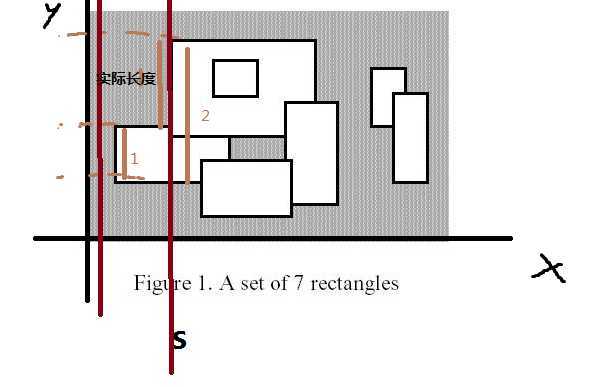
这是第二道关于扫描线的题目，自己想了想但是还是没有想通为什么，然后开了别人的博客想明白了，总的来说和面积并类似，但是这里求的是周长并。
这里多了一个域。
具体看图
如果是将区间映射到Y轴上，以图中的棕色线为扫描线(从左往右扫)
那么每扫一跳线，纵向增加的长度为 当前扫到的长度减去前一条线的长度 sum[i] - sum[i-1],如图，扫描到s时，纵向增加实际长度应该为 sum[2] - sum[1];
那么，横向增加的长度怎么算呢，这个就有点麻烦了，这里增加了一个域，num[i]，用来存放此区间内不想交(或者说不互相覆盖)的矩形的个数。
那横向增加的长度 = num[i]*2*(Line[i+1].x - Line[i].x) 
这里的2是因为有上下两条线。
这样每次扫描ret增加是 ret += { abs(sum[i]-sum[i-1]) + num[i]*2*(Line[i+1].x - Line[i].x) }
那么这道题就能解决了。置于那个num[]阈，如果lson的右端点 > rson的左端点，肯定就有重合了。

#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
#define mid(l,r) (l + r) >> 1
#define inf 0x3f3f3f3f
#define maxn 5005
#define clr(a,b) memset(a,b,sizeof(a))

struct Line
{
    int x, y1, y2;
    int fl;
    Line() {}
    Line(int a,int b,int c,int d) : y1(a), y2(b), x(c), fl(d) {}
    bool operator < (const Line & m) const
    {
        if(x == m.x)    return fl > m.fl;
        return x < m.x;
    }
};

Line L[maxn<<1];
int sum[maxn<<3];
int cov[maxn<<3];
int num[maxn<<3];
//int coo[maxn<<3];
bool lf[maxn<<3],rg[maxn<<3];

void PushUp(int l,int r,int rt)
{
    if(cov[rt])
    {
        lf[rt] = rg[rt] = 1;
        sum[rt] = r - l + 1;
        num[rt] = 2;
    }
    else if(l == r)
    {
        lf[rt] = rg[rt] = 0;
        sum[rt] = 0;
        num[rt] = 0;
    }
    else
    {
        lf[rt] = lf[rt<<1];
        rg[rt] = rg[rt<<1|1];
        sum[rt] = sum[rt<<1] + sum[rt<<1|1];
        num[rt] = num[rt<<1] + num[rt<<1|1];
        if(lf[rt<<1|1] && rg[rt<<1])   num[rt] -= 2;
    }
}

void Update(int L,int R,int c,int l,int r,int rt)
{
    if(L <= l && r <= R)
    {
        cov[rt] += c;
        PushUp(l,r,rt);
        return;
    }

    int m = mid(l,r);
    if(L <= m)  Update(L,R,c,lson);
    if(R >  m)  Update(L,R,c,rson);
    PushUp(l,r,rt);
}

int n,x1,x2,y1,y2;


int main()
{
    scanf("%d",&n);
    int cnt = 0;
    int lf = 10000, rg = -10000;
    clr(sum,0),clr(num,0);
    for(int i=0;i<n;i++)
    {
        scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
        lf = min(lf,y1);
        rg = max(rg,y2);
        L[cnt++] = Line(y1,y2,x1,1);
        L[cnt++] = Line(y1,y2,x2,-1);
    }

    sort(L,L+cnt);

    int ret = 0, pre = 0;
    for(int i=0;i<cnt;i++)
    {
        if(L[i].y1 < L[i].y2)   Update(L[i].y1, L[i].y2-1,L[i].fl,lf,rg-1,1);
        ret += (abs(sum[1] - pre) + (L[i+1].x - L[i].x)*(num[1]));
        pre = sum[1];
    }
    printf("%d\n",ret);


    return 0;
}

代码君

·专题」线段树,布布扣,bubuko.com

·专题」线段树

标签：style blog http color 使用 strong

原文地址：http://www.cnblogs.com/BigBallon/p/3710513.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行

·专题」 线段树

·专题」线段树