标签:
(1)长方体A想绕(10,3,4)旋转50°且沿着x方向放大2倍且向(9,-1,8)方向平移2个单位,那么经过上面的变换后,新的长方体各个点的坐标是多少呢?应用矩阵可以很轻松的算出答案。
(2)知道子坐标系在父坐标系中的位置,可以求出子坐标系中的店在父坐标系中的位置。
矩阵能描述任意线性变换。线性变换保留了直线和平行线,线性变换保留直线的同时,其他的几何性质如长度、角度、面积和体积可能被变换改变了。简单的说,线性变换可能“拉伸”坐标系,但不会“弯曲”或“卷折”坐标系。
(1)平移
以下矩阵能把一点向t矢量方向平移:
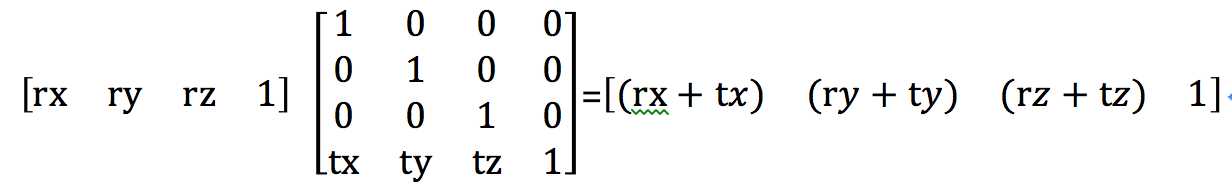
(2)旋转

正方向为从旋转轴正向看过去的逆时针方向,比如绕z轴[0,0,1]旋转,正方向为x至y轴方向
知道了绕着三轴后的旋转矩阵,那么下面就是绕任意向量所得的矩阵了。设M为单位矩阵经向量a旋转后的矩阵,且a = (xa, ya, za),旋转角度为α,则
M=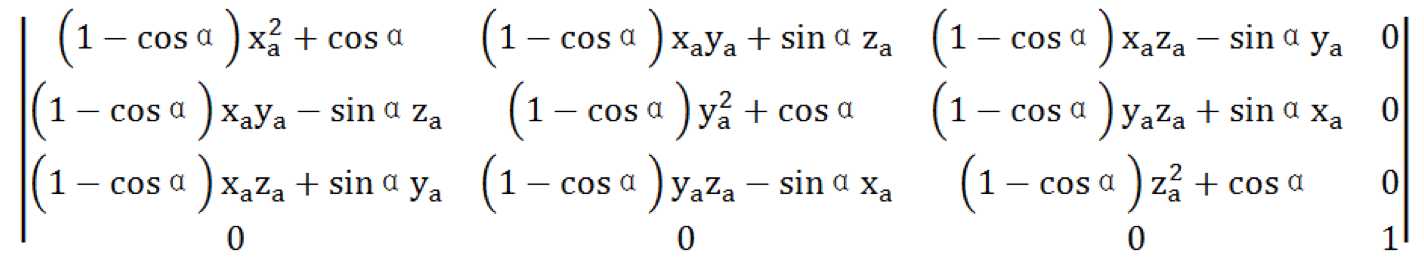
不要问为什么,记住即可。
(3)缩放
缩放点为r,X轴缩放sx,y轴缩放sy,z轴缩放sz,则新坐标为:
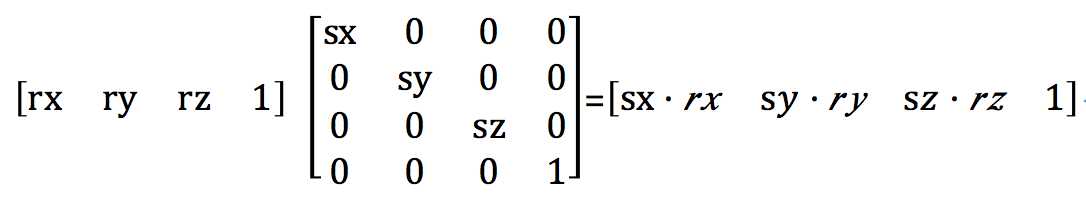
(4)综合
比如要把坐标系中的所有点平移[2,3,4](X轴平移2,y轴平移3,z轴平移4)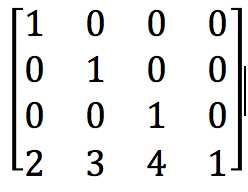 ,
,
绕z轴旋转90°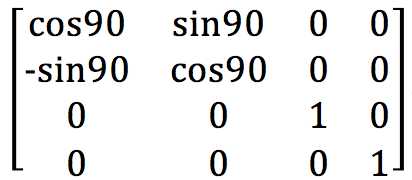 ,
,
x,y,z轴都放大2倍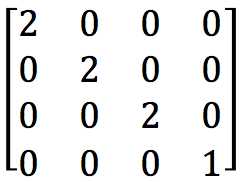 ,
,
则得到的变换矩阵为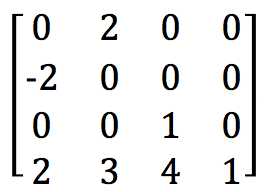
注意:缩放不是只把sx,sy,sz位置相乘,而是那一轴的模为缩放值
最后所得的变换矩阵 不等于
不等于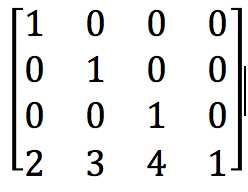
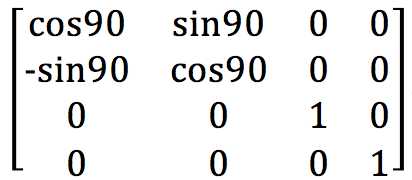
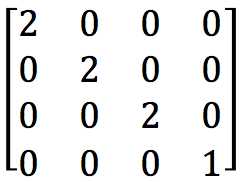 相乘
相乘
把点或方向从任何子坐标系C变换至父坐标系P的矩阵,可写作Mc-p。此矩阵表示把点或方向从子空间变换至父空间。以下等式把任何子空间位置矢量Pc变换至父空间位置矢量Pp,Pp = PcMc-p
Mc-p = 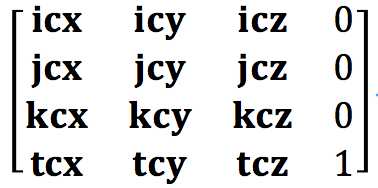
jc为子空间y轴的单位基矢量,此矢量以父空间坐标表示
kc为子空间z轴的单位基矢量,此矢量以父空间坐标表示
OpenGl超级宝典第四版P101页说:如果一个4×4矩阵包含了一个不同的坐标系统的位置和方向(可以看成上面的Mc-p),那么,把一个顶点Pp与这个矩阵相乘,其结果就是一个变换到该坐标系统的新顶点Pc(坐标还是相对于原坐标系)。这看起来像公式Pc =Pp Mc-p ,错错错!这用Pp完全是个误导,把Pp改名字叫A,坐标V,由于是线性变换,所以在新坐标系统中A的坐标还是V,所以这就与Pp = PcMc-p 一致了,Pp为A在新坐标系统中V在原坐标系中的坐标。
OpenGl中矩阵的变换是叠加的,每做一次矩阵变换,就把零点移到新的坐标系中。下次变换只影响当前坐标系及其子坐标系,不会影响其父坐标系。载入单位矩阵是将零点重新置为最初的零点。
单纯的矩阵运算不会移动零点位置,所以与单位矩阵相乘没有任何效果。
1.OpenGl超级宝典第四版P101
2.游戏引擎架构P151
3. OpenGL中glRotatef()函数究竟对矩阵做了什么
4.3D数学 ---- 矩阵的几何解释 - 天行健 君子当自强而不息 - C++博客
标签:
原文地址:http://www.cnblogs.com/BigFeng/p/4970388.html