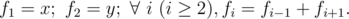Codeforces Round #257 (Div. 2)B 矩阵快速幂

Jzzhu has invented a kind of sequences, they meet the following property:

$bubuko.com,布布扣$

You are given x and y, please calculate fn modulo 1000000007 (109?+?7).

Input

The first line contains two integers x and y (|x|,?|y|?≤?109). The second line contains a single integer n (1?≤?n?≤?2·109).

Output

Output a single integer representing fn modulo 1000000007 (109?+?7).

Sample test(s)

input
2 3
3

output
1

input
0 -1
2

output
1000000006

Note

In the first sample, f2?=?f1?+?f3, 3?=?2?+?f3, f3?=?1.

In the second sample, f2?=??-?1; ?-?1 modulo (109?+?7) equals (109?+?6).

题解

很简单的一个递推法的题目，我直接用矩阵快速幂去过了。

构造方法也很简单。

f1 + f3 = f2

f3 = f2 - f1

f3 = 1 * f2 + -1 * f1

f2 = 1 * f2 + 0 * f1

所以矩阵就是

1， -1

1， 0

然后就是取模运算和负数处理了。负数取模会返回负数。因为我是快速幂的写法，最后返回的数一定是在(-Mod, Mod)之间的，所以直接加上一个Mod，然后再取一次模就好了。

代码示例

/******************************************************************************
*       COPYRIGHT NOTICE
*       Copyright (c) 2014 All rights reserved
*       ----Stay Hungry Stay Foolish----
*
* @author		:Shen
* @name         :B
* @file         :G:\My Source Code\【ACM】比赛\0719 - CF\B.cpp
* @date         :2014/07/19 20:57
* @algorithm    :Matrix Fast Power Method
******************************************************************************/

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long int64;

const int MAXN = 2;
const int MAXM = 2;
const int Mod = 1000000007;

struct Matrax{
    int n, m;
    int64 mat[MAXN][MAXM];
    Matrax(): n(-1), m(-1){}
    Matrax(int _n, int _m): n(_n), m(_m){
        memset(mat, 0, sizeof(mat));
    }
    void Unit(int _s){
        n = _s; m = _s;
        for (int i = 0; i < n; i++){
            for (int j = 0; j < n; j++){
                mat[i][j] = (i == j)? 1: 0;
            }
        }
    }
    void print(){
        printf("n = %d, m =  %d\n", n, m);
        for (int i = 0; i < n; i++){
            for (int j = 0; j < m; j++)
                printf("%8d", mat[i][j]);
            printf("\n");
        }
    }
};

Matrax add_mod(const Matrax& a,const Matrax& b,const int64 mod){
    Matrax ans(a.n, a.m);
    for (int i = 0; i < a.n; i++){
        for (int j = 0; j < a.m; j++){
            ans.mat[i][j] = (a.mat[i][j] + b.mat[i][j]) % mod;
        }
    }
    return ans;
}

Matrax mul(const Matrax& a,const Matrax& b){
    Matrax ans(a.n, b.m);
    for (int i = 0; i < a.n; i++){
        for (int j = 0; j < b.m; j++){
            int64 tmp = 0;
            for (int k = 0; k < a.m; k++){
                tmp += a.mat[i][k] * b.mat[k][j];
            }
            ans.mat[i][j] = tmp;
        }
    }
    return ans;
}

Matrax mul_mod(const Matrax& a, const Matrax& b, const int mod){
    Matrax ans(a.n, b.m);
    for (int i = 0; i < a.n; i++){
        for (int j = 0; j < b.m; j++){
            int64 tmp = 0;
            for (int k = 0; k < a.m; k++){
                tmp += (a.mat[i][k] * b.mat[k][j]) % mod;
            }
            ans.mat[i][j] = tmp % mod;
        }
    }
    return ans;
}

Matrax pow_mod(const Matrax& a, int64 k, const int mod){
    Matrax p(a.n, a.m), ans(a.n, a.m);
    p = a; ans.Unit(a.n);
    if (k==0) return ans;
    else if (k==1) return a;
    else {
        while (k){
            if (k & 1){
                ans = mul_mod(ans, p, mod);
                k--;
            }
            else {
                k /= 2;
                p = mul_mod(p, p, mod);
            }
        }
        return ans;
    }
}

int64 x, y, n, res;

void solve(){
    cin >> x >> y >> n;
    if (n == 1) res = x;
    else if (n == 2) res = y;
    else
    {
        Matrax ans(2, 1);

        //tmp = cef ^ (n - 2);
        //ans = tmp * beg;
        //res = ans.mat[0][0];

        Matrax cef(2, 2);
        cef.mat[0][0] = 1; cef.mat[0][1] = -1;
        cef.mat[1][0] = 1; cef.mat[1][1] =  0;
        //cef.print();

        Matrax beg(2, 1);
        beg.mat[0][0] = y; beg.mat[1][0] = x;

        Matrax tmp(2, 2);
        tmp = pow_mod(cef, n - 2, Mod);
        //tmp.print();

        ans = mul_mod(tmp, beg, Mod);
        //ans.print();
        res = ans.mat[0][0];
    }
    if (res < 0) res += Mod;
    cout << res << endl;
}

int main()
{
    solve();
    return 0;
}

原文地址：http://blog.csdn.net/polossk/article/details/37974211