标签:
随着数字化技术的快速发展,电话、手机、相机、电视等数字化产品如雨后春笋般涌现市场,无时无刻不在影响着我们的生活,这是一个数字化的时代。

在这样一个数字化时代,所有的数字信号采集都必须有相应的数字化的软硬件支撑。随着人们对于图像、视频等多媒体内容的需求和要求越来越高,对应的硬件设备如照相机、摄像机等信号采集的设备的压力也越来越大。比如,相片的分辨率越来越高,这就需要在照相机中内置越来越多的传感器,以采集质量更高的图像信号。此外还有其他一些目前传统信号采集方式无法有效满足的需求,不可见光如X射线、伽马射线等信号采集、高速视频采集等。

那么,在这样一个对信号采集越来越苛刻的需求下,有没有一种更有效的采集、传输、存储以及处理的方法呢?答案就是压缩感知。
首先,我们来了解一下传统的信号采集方法。
传统的数字信号采样定律就是有名的香农采样定理,又称那奎斯特采样定律,定理内容如下:
为了不失真地恢复模拟信号,采样频率应该不小于模拟信号频谱中最高频率的2倍。
下图分别为在时域和空域上的数字化采集。
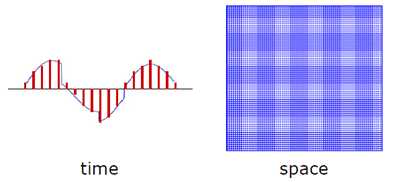
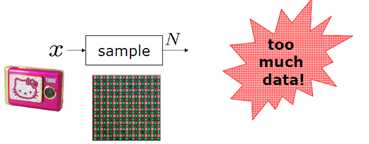
基于香农采用定理,我们来看看目前传统图像信号采集设备的采样过程:
- 按照Nyquist采样率进行均匀采样,得到可以无失真恢复模拟信号的数字信号;uniformly sample data at Nyquist rate (2x Fourier bandwidth)
信号存在冗余,即信号具有稀疏性:
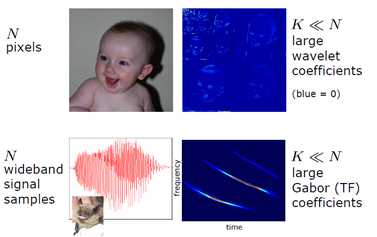
2、上述步骤得到的数字信号的数据量比较大,一方面不利于存储和传输,另一方面该数字信号本来存在很多冗余,可以对其进一步的压缩,于是就通过各种编码方法对数据进行有效的压缩;compress data
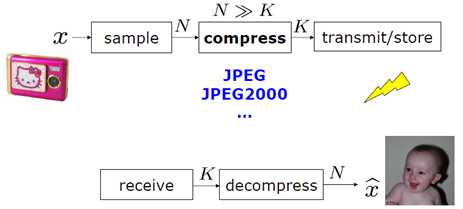
我们来分析一下上面的采样过程有什么不妥的地方?
相机的传感器通过将模拟信号(光)转换为数字信号(Nyquist定理采样),如N pixel的图像信号,之后又通过压缩编码算法将N pixel的图像信号转化为K个系数表示的数据,而K<<N,那么问题来了,为什么我们费了一番心思获得了N个采样值,却最后又通过复杂的编码算法将之压缩成K个数值?
基于这个疑问,我们引出了压缩感知的概念。
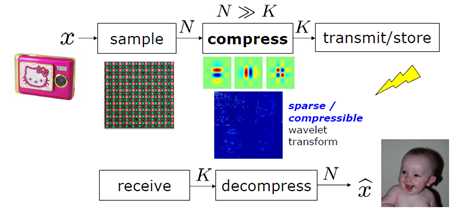
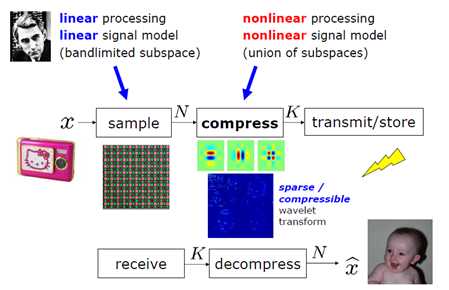
顾名思义,就是感知压缩,直接获取压缩后的数据。即在采集的时候,直接采集有效的M个测量值,而非满足Nyquist采样定理的N个采样值(M<<N)。
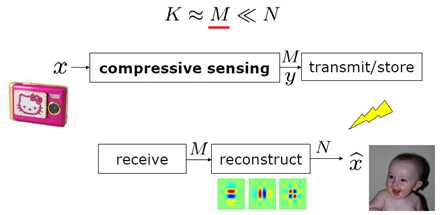
当信号是稀疏或可压缩的,我们可以以某个线性投影的方式来得到信号的压缩后表示condensed representation,(采集过程:降维)得到的数据能够以无失真或较低失真地方式重建原始的数字信号。(重建过程)
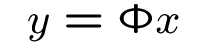
Y就是压缩后的信号表示
X代表原始的数字信号
采集过程就是一个线性投影过程,如上面的公式所示。
下图形象地描述了这个过程,Φ的每一行代表一次测量,M行则可以得到M个测量值。
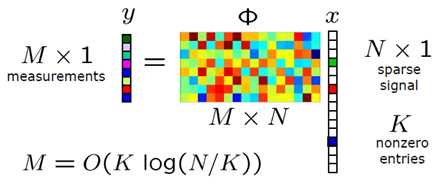
压缩感知的采集过程如下:
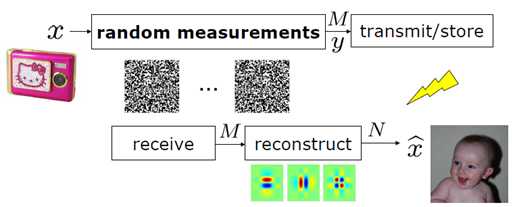
接下来,我们来分析一下,为什么这样的一种采集方式是有效的?
随机投影矩阵Φ并不是满秩的(M<N),因此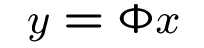 公式的左边两边并不是等价的过程,即已知y,不能直接求得x,可以说是存在信息损失的。
公式的左边两边并不是等价的过程,即已知y,不能直接求得x,可以说是存在信息损失的。
但是,随机投影矩阵在很大概率上保留了稀疏信号的结构和信息,即得到测量值y之后,我们可以以很大的概率来完美重建信号。
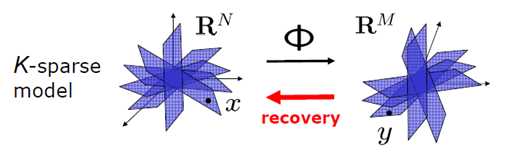
了解了压缩感知的大致框架之后,我们从数学角度来考虑压缩感知这个问题。
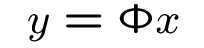
从上面这个采集公式可以得出压缩感知的三个必要条件:
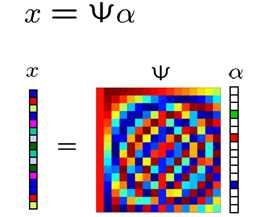

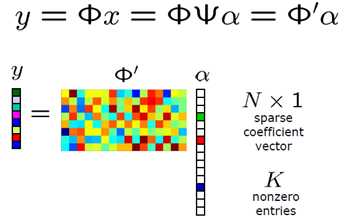
通过利用信号稀疏性的先验知识,压缩感知采用了一种全新的数据采集方式。
标签:
原文地址:http://www.cnblogs.com/AndyJee/p/4973670.html