标签：
对于常规线性模型来说，其精确的模型可定义如下：
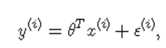
其中，模型中的第一部分描述了通过待预测值随自变量的变化趋势，而第二部分描述了线性模型不能建模的误差项。
最小二乘方法采用损失代价和最小来获得线性模型的参数。在此，我们通过假设误差项的概率分布，并用最大似然估计的方法寻求模型参数Θ。
在此，我们假设误差项ε是独立同分布的，并且符合均值为0的高斯分布，即：
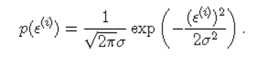
则，待预测值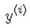
也服从均值为
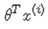的高斯分布：
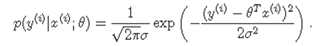
上式可理解为当给定X，Θ时，待预测值y的概率分布，我们同时也可以给出Θ的似然函数：
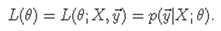
由于不同观测点的误差项服从独立同分布，因此整体似然函数可写为：
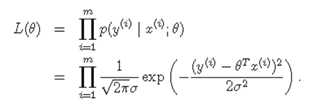
根据最大似然估计的思想，求似然值的log最大化，可得：
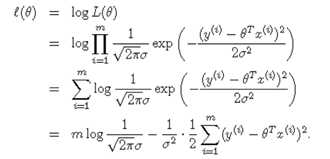
即为：
?
?
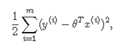
注：在此主要用到了最大似然估计的知识，并且给定了前提，即误差项服从独立高斯同分布。
关于最大似然估计，这里有一个讲的非常好的文章。http://blog.csdn.net/yanqingan/article/details/6125812
标签：
原文地址：http://www.cnblogs.com/shibalang/p/4974583.html
