标签:
1 排列组合回顾:
排列数:Amn=n!(n?m)!排列的总的个数每次排列个数的全排列=AmnAmm=组合数
LCS求长度为五的字符串的子序列有多少个?
N=C15+C25+C35+C45+C55=A15A11+A25A22+A35A33+A45A44+A55A55
根据初中的二次项展开定理:
(a+b)n=∑r=0nCrnan?rbr(1+x)n=C0nx0+C1nx1+C2nx2+...+Cmnxm+...+Cnnxnx=1时:N=2n?1=C1n+C2n+...+Cmn+...+Cnn
2 幂级数
(1+x)n的各阶导数=?????????????????ffff(x)(0)=1(x)(1)=n?(1+x)n?1(x)(2)=n?(n?1)?(1+x)n?2...(x)(m)=n?(n?1)?(n?2)...(n?m+1)(1+x)m?1
2.1 级数展开:
(1+x)n(1+x)n对于n=12、?12的情况:(1+x)12(1+x)?12====1+n?x+n?(n?1)2!x2+...+n?(n?1)...(n?m+1)m!xm+...;当x∈(?1,1)时候,此级数收敛于(1+x)n①,在区间的端点处,展开式是否也收敛到(1+x)n这个函数要看n的数值而定。C0nx0+C1nx1+C2nx2+...+Cmnxm+...+Cnnxn当n为正整数时候,它的幂级数展开式就是x的n次多项式,这就是代数学中的二项定理(证明请直接写出级数展开式和二项展开式做对比,或者按《高数下》函数展开成幂级数P220证明),所以此时x不仅在端点?1,1处成立,在整个实数域内都成立,因为它就直接等于(1+x)n。1+12x?12?4x2+1?32?4?6x3?1?3?52?4?6?8x4+....;(?1≤x≤1)1?12x+12?4x2?1?32?4?6x3+1?3?52?4?6?8x4+....;(?1<x≤1)
上面说某级数收敛到函数f(x),需要看清楚条件。
当(1+x)^n,n为正整数的时候,这个函数的幂级数展开就是它的二项展开所以可以有如下应用
当x=1时:(1+x)n=2n=1+C1n+C2n+...+Cmn+...+Cnn==>C1n+C2n+...+Cmn+...+Cnn=2n?1
但下列用法是错误的:
因为已知如下函数的幂级数展开:
11?x=1+x+x2+...+xn+...;(?1<x<1)
所以
1+2+4+8=8(18+28+48+1)=8(11?12)=16
注意,这里级数收敛的意思是:当n趋于无穷的时候,这个展开式的和收敛到函数11?x。当n很小时,就可能离函数11?x的值很远。而上面那个例子可以用,是因为n为正整数时,它的展开式恰好等于它的二项展开式,二项展开式就等于函二项式本身,所以上一个例子应该叫二项展开式的应用,更为合理。
2.2 其它重用的幂级数
sinx=x?x33!+x55!...+(?1)n?1x2n?1(2n?1)!+..;(?∞<x<+∞)cosx=1?x22!+x44!+...+(?1)nx2n?1(2n?1)!+..;(?∞<x<+∞)ex=1+x+x22!+...+xnn!+...;(?1<x<1)
3 数列求和
3.1 等比数列求和
SqS相减:(1?q)S两边同时除以1?q,即得:S====a+aq+aq2+aq3+.+aqnaq+aq2+aq3+.+aqn+aq(n+1)a?aq(n+1)a[1?q(n+1)]/(1?q)
3.2 等差数列求和
倒序相加:
S3S32S3S3Sn=====3+4+5+66+5+4+33?(3+6)frac3?(3+6)2n(a0+an)2
4 集合的容斥原理
说有三个集合A、B、C,若集合中元素个数用Card(集合名)表示,那么Card(A∪B∪C)怎么求?
方法很简单,就是Card(A∪B∪C=Card(A)+Card(B)+Card(C)-Card(A∩B)-Card(B∩C)-Card(A∩C)+Card(A∩B∩C)所谓的容斥原理,如下图
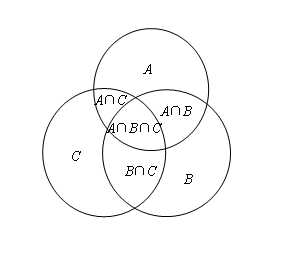
当然两个集合更容易计算,即Card(A∪B)=Card(A)+Card(B)-Card(A∩B)
那四个集合呢?
四个集合的图是这样的
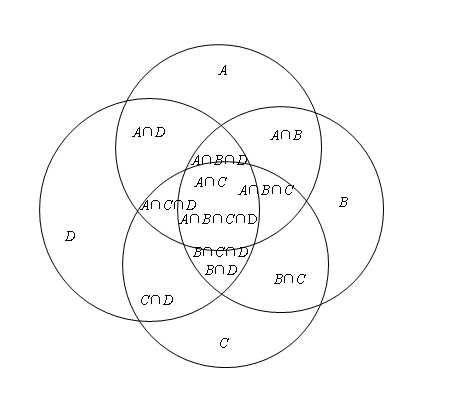
看着比较乱, 考虑到比三个集合多一个,可以用Card(A∪B∪C∪D)=Card(A∪B∪C)+Card(D-A∪B∪C)就可以了,因为新插入一个集合,这样与D相关的集合就有了A∩D、B∩D、C∩D,由容斥原理,这三个集合的并集元素个数为
Card((A∩D)∪(B∩D)∪(C∩D))=Card(A∩D)+Card(B∩D)+Card(C∩D)-Card(A∩B∩D)-Card(A∩C∩D)-Card(B∩C∩D)+Card(A∩B∩C∩D)
所以
Card(D-A∪B∪C)==Card(D)-Card((A∩D)∪(B∩D)∪(C∩D))Card(D)-Card(A∩D)-Card(B∩D)-Card(C∩D)+Card(A∩B∩D)+Card(A∩C∩D)+Card(B∩C∩D)-Card(A∩B∩C∩D)
===>
Card(A∪B∪C∪D)==Card(A∪B∪C)+Card(D-A∪B∪C)Card(A)+Card(B)+Card(C)+Card(D)-Card(A∩B)-Card(A∩C)-Card(A∩D)-Card(B∩C)-Card(B∩D)-Card(C∩D)+Card(B∩C∩D)+Card(A∩C∩D)+Card(A∩B∩D)+Card(A∩B∩C)-Card(A∩B∩C∩D)
我们可以发现容斥原理的规律:
如果给定n个集合A(1),A(2),…,A(n),那么
Card(A(1)∪A(2)....∪A(n))=∑inCard(A(i))-∑1≤i<j≤nCard(A(i)∩A(j))+∑1≤i<j<k≤nCard(A(i)∩A(j)∩A(k))-,…,+(?1)n?1?Card(A(1)∩A(2)....∩A(n))
数学基础知识
标签:
原文地址:http://www.cnblogs.com/gavin-yue/p/4975547.html

