勒让德符号相关

　　小西瓜最近学了这个东西，并不很懂，就想敲篇日志巩固一下……
     勒让德符号嘛，很有趣（本句扯淡），它呢，跟平方剩余有关：设a,b是两个非零整数，b为素数，我们定义符号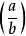：若存在整数x, 使得，那么就记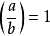; 否则就记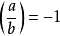。 当p|a时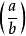，=0。（这符号敲起来有点麻烦诶，为方便，下面用(a\b)表示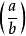，方向与除号相反）

      一些性质：

      首先，由欧拉判别条件，显然有(a\b)≡a^((b-1)/2)(mod b)

      若a1≡a2 那么(a1\p)=(a2\p)，证明显然，套下欧拉判别条件就行。
      显然……(-1\p)=(-1)^((p-1)/2)

　　然后，好像想不出什么性质了……

    那么进入正题吧，接下来是……高斯引理：
      若p为素数，(a,p)=1，记μ为数列a,2a,3a……,[(p-1)/2]a的最小正剩余中大于(p-1)/2的数个数，那么(a\p)=(-1)^μ，证明(感觉跟费马小定理证明方法有点像)：

    用r1,r2,r3……rk表示数列中最小正剩余不大于(p-1)/2的数，s1,s2,s3……sμ就是剩下的数，下面证明{r}，p-{s}（对{s}中每个数，都对p取差）这两个数列中各数关于模p两两不互余：
     对于处于同一个数列中的数，结论是显然的（参见费马小定理证明）。设，ri≡p-sj(mod p)，则p|(ri+sj)，记ri=ua，si=va，则p|((v+u)a)，由于(a,p)=1，所以p|(v+u)，但是v+u<p，这是不可能的，所以得证。

     那么显然，数列{r}， p-{s}就变成1,2,3,……,(p-1)/2的一个排列，那么我们把{r}，{s}给连乘起来，得到r1*r2*r3……rk*s1*s2*s3……sμ≡(-1)^μ((p-1)/2)!(mod p)，即a*2a*3a*……((p-1)/2)a≡(-1)^μ*((p-1)/2)!(mod p)，于是a^((p-1)/2)≡(-1)^μ(mod p)，于是(a\p)=(-1)^μ。

    终于完了……
     高斯引理是个神奇的东西，做题的时候经常可以用到。

     高潮到了！接下来是二次互反律（如果说我已经完全懂了，那是在忽悠你） ：

     设p，q为两个不同奇素数，那么(p\q)(q\p)=(-1)^((p-1)/2+(q-1)/2)，前面内容同高斯引理证明，我们接下去讨论：

     记R=Σr ，S=Σs，那么Σr+Σ(p-s)=R+μp-S，由于在证高斯引理的时候已经说过，r1,r2,r3…rk,p-s1,p-s2,...p-sμ是1,2,3,..,(p-1)/2的一个排列，那么(1/2)*((p-1)/2)*((p-1)/2+1)=(p²-1)/8=R+μp-S，然后可以很容易推得R=S-μp+(p²-1)/8。

    接下来，考虑所有式子：iq=[iq/p]p+ti(带余除法)，如果将这些式子关于i求和，q∑i=pΣ[iq/p]+∑ri+∑si，也就是q(p²-1)/8=pΣ[iq/p]+R+S，将R=S-μp+(p²-1)/8代人，得q(p²-1)/8=pΣ[iq/p]+2S-μp+(p²-1)/8，即(q-1)(p²-1)/8=p(Σ[iq/p]-μ)+2S。

    因为(q-1)(p²-1)/8是偶数（q-1是偶数，(p²-1)/8是整数）2S也是偶数，于是Σ[iq/p]-μ必为偶数，从而Σ[iq/p]-μ可得：(-1)^Σ[iq/p]=(-1)^μ=(q\p)，由于p，q等价，那么(-1)^Σ[ip/q]=(-1)^μ=(p\q)，相乘得到(p\q)(q\p)=(-1)^Σ[iq/p]*(-1)^Σ[ip/q]。

    下面证明 Σ[jp/q]+Σ[iq/p]=((p-1)/2+(q-1)/2)。取((p-1)/2)*((q-1)/2)个数，jp-iq，显然其中没有0（反证法），那么考虑其中的正数，对于每个给定的j，满足jp>iq的i共有[jp/q]个，又j小于等于(q-1)/2，所以正数个数为Σ[jp/q]，同理，负数个数为Σ[iq/p]，于是得证Σ[jp/q]+Σ[iq/p]=((p-1)/2+(q-1)/2)，从而(p\q)(q\p)=(-1)^((p-1)/2+(q-1)/2)即二次互反律成立。

    二次互反律最先由欧拉提出，由高斯在19 岁时首次证明，现在，二次互反律已有超过200种证明，这是18世纪数论的创举。
      呼，于是乎，今天我在极吵闹的环境下完成了两篇日志，累成DOG……以此纪念我在金中的小高一生涯的开端……

    完……