标签:
主要内容:
在DSP(数字信号处理)中,有个很重要的概念:变换域(某个线性空间:一组基函数支撑起来的空间)
一般而言,我们的信号都是在时域或空域中来表示,其实我们可以在其他变换域中通过某些正交基函数的线性组合来表示信号。如:sinusoids, wavelets, curvelets, Gabor functions,. . .
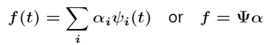
对于某个变换域或空间,其基函数是确定的,只要得到系数α的这一组值,即可通过该系数向量来表示信号。
那么系数α该怎么求呢?
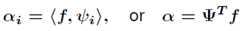
说了这么多,为什么要通过变换域的系数来表示信号呢?
很明显,系数向量α的大小远小于原始信号,这一个压缩和降维的过程(稀疏性),有利于存储、传输和处理。
下面以图片为例,介绍传统的图像表示方法DCT和现代的图像表示方法小波变换:
Classical Image Representation: DCT
Discrete Cosine Transform (DCT)
Basically a real-valued Fourier transform (sinusoids)

如上图所示,左边为原始图像,右边为DCT变换后的图像。
该图像表示二维的频率幅值系数,可以看出,右下角的大部分系数接近于0。也就是说图像的大部分能量都集中在左上角的低频部分(稀疏性),
因此我们只要保留左上角的信息(压缩),就可以很好地重建出左边的图像。(有损)
这也就是JEPG图像压缩标准的基础:DCT变换。
DCT重建(反变换)的图像特点:平滑区域表现很好,边缘可能会模糊或出现振铃(因为某些高频信号丢失)
Modern Image Representation: 2D Wavelets
有关小波变换的知识,这里就不详述,可以参考:http://www.zhihu.com/topic/19621077/top-answers

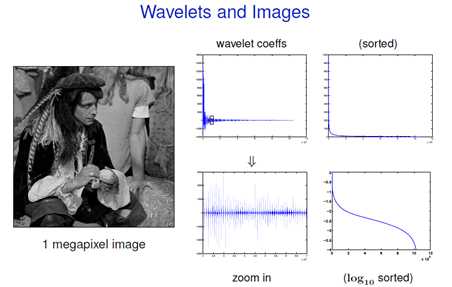
如上图所示,左边为原始图像,中间为尺度图像,右边为小波变换后的系数结构
系数框架:大系数很少,小系数很多(稀疏性)
这也是JPEG2000压缩标准的基础:小波变换。
小波变换重建(反变换)的图像特点:平滑区域表现很好,边缘更加尖锐(在边缘处理上,比DCT好)
小波系数的分布:
小波变换的重建:
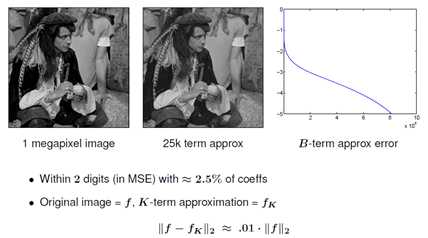
这一部分主要介绍了变换域,以及信号在变换域的稀疏表示,并以图像的DCT和小波变换为例,来阐述信号在变换域的稀疏性。
稀疏性的作用总结:
跟传统采集不同,压缩感知采集的不是像素点,而是一组线性组合的测量值。
下面的公式表示每一个测量值yi的计算过程,f表示信号,Φ表示测量矩阵,两者的内积之和即为yi。
经过M次测量之后,即得到所需要的M个测量数据Y。
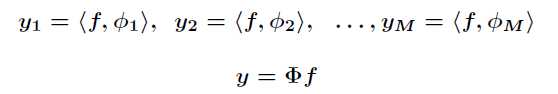
问题是测量矩阵应该怎么选择呢?

为了能够重构信号,测量矩阵的选择尤其重要,矩阵需要满足与信号的稀疏表示基Ψ不相关。(RIP性质,具体不详述)
实验证明:高斯随机矩阵、一致球矩阵、二值随机矩阵、局部傅立叶矩阵、局部哈达玛矩阵以及托普利兹矩阵等能在很大概率上满足上述条件。
测量公式如下:

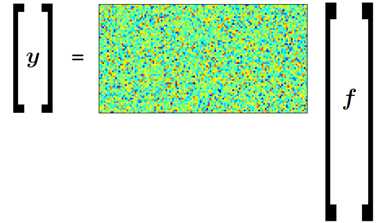
假设信号是K-sparse,测量矩阵是高斯随机矩阵,现在通过采集获得了M个测量值,我们如何恢复出我们的信号呢?
测量过程:
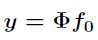
重建过程:(数学建模:L1 Minimization,当然还有其他方法,后续再叙述)
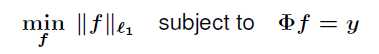
需要多少个测量值才能够有效地恢复出信号呢?一个、两个很明显是不行的,N个显然就没有了压缩的意义,那么至少多少才合适呢?
下面的公式给出了一个估计值:
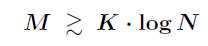
变换域重建:

举例:

标签:
原文地址:http://www.cnblogs.com/AndyJee/p/4981161.html