标签:
0. 概要
最近公共祖先,指的是在一颗有根树上,两个点的公共祖先中,深度最大的那个。
最直接的应用是求无权树上两个点的最短距离:$distance(u, v) = depth(u) + depth(v) - 2depth(lca(u, v))$。
再有其他的应用则以后再提。
1 基于 dfs 序列上 RMQ 的稀疏表解法
首先 dfs 遍历树,如下如图中蓝色箭头的顺序。并记录:
1. 遍历点序列 $euler[] = \{1, 2, 1, 3, 5, 3, 6 ……$
2. 每个点首次在 euler 中出现的位置,$firstIn[1] = 0, firstIn[2] = 1, firstIn[3] = 3 ......$
3. 每个点的深度,$depth[1] = 0, depth[2] = 1, depth[3] = 1, ......$
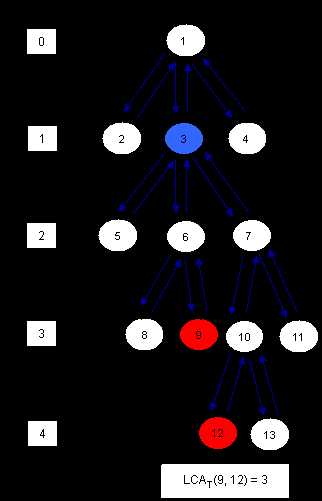
有了这些我们就可以发现两个点的 lca 其实并不难求,比如 9 和 12 的 lca 是多少?首先在 dfs 的过程中,这个点一定在 9 和 12 之间被访问了。其次,这个点是这之中访问的点中深度最小的。
所以,只要在 firstIn[9] 到 firstIn[12] 之间的 euler[] 中,找到深度最小的点就可以了。
这就转换成了一个 RMQ 问题。
因为这个 RMQ 问题不需维护更改,一般我们用稀疏表来解决。
/*
子内容:稀疏表。
稀疏表是一种解决 RMQ 问题的有效手段,可以做到 $O(n \log(n))$ 预处理,$O(1)$ 询问区间最小(大)值。
具体做法是这样的。待处理的数组如果是 A[],这个时候用一个辅助数组 B[][],B[i][j] 表示 A[j] 开始,长度为 $2^i$ 的子串的最值。
比如,B[2][4] 表示 A[4] A[5] A[6] A[7] 的最值;B[0][i] 就等于 A[i]。
利用递推的方法可以 $O(n \log(n))$ 处理出来这个表。
查询一个区间 [l, r] 的最值时,令 $k = log_2(r - l + 1)$,这样只需要 $B[k][l]$ 和 $B[k][r - 2^{i-1} + 1]$ 比较就可以得到结果。
*/
2. tarjan
这个是一个离线算法,需要用并查集维护。
具体介绍请看这里:http://noalgo.info/476.html 此人讲的很清楚,我就不多废话了。
此外还有倍增的方法,但是我没用过。
标签:
原文地址:http://www.cnblogs.com/gu-castle/p/4992080.html