标签:codeforces 矩阵快速幂
题目链接:http://codeforces.com/problemset/problem/450/B
----------------------------------------------------------------------------------------------------------------------------------------------------------
欢迎光临天资小屋:http://user.qzone.qq.com/593830943/main
----------------------------------------------------------------------------------------------------------------------------------------------------------
Jzzhu has invented a kind of sequences, they meet the following property:
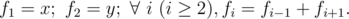
You are given x and y, please calculate fn modulo 1000000007 (109?+?7).
The first line contains two integers x and y (|x|,?|y|?≤?109). The second line contains a single integer n (1?≤?n?≤?2·109).
Output a single integer representing fn modulo 1000000007 (109?+?7).
2 3 3
1
0 -1 2
1000000006
In the first sample, f2?=?f1?+?f3, 3?=?2?+?f3, f3?=?1.
In the second sample, f2?=??-?1; ?-?1 modulo (109?+?7) equals (109?+?6).
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
struct A
{
int mat[2][2];
};
A d,f;
__int64 n,mod;
A mul(A a,A b)
{
A t;
memset(t.mat,0,sizeof(t.mat));
for(int i=0;i<n;i++)
{
for(int k=0;k<n;k++)
{
if(a.mat[i][k])
for(int j=0;j<n;j++)
{
t.mat[i][j]+=a.mat[i][k]*b.mat[k][j];
t.mat[i][j]%=mod;
}
}
}
return t;
}
A quickP(int k)
{
A p = d ,m;
memset(m.mat,0,sizeof(m.mat));
for(int i=0;i<n;++i)//单位矩阵
{
m.mat[i][i]=1;
}
while(k)
{
if(k & 1)
m=mul(m,p);
p=mul(p,p);
k >>= 1 ;
}
return m;
}
int main()
{
n=2;
int k,t;__int64 x,y,z;
while(scanf("%I64d%I64d",&x,&y)!=EOF)
{
int s=0;
scanf("%I64d",&z);
mod=1000000007;
if(z == 1)
{
if(x < 0)
printf("%I64d\n",x+mod);
else
printf("%I64d\n",x);
continue;
}
d.mat[0][1]=-1;d.mat[1][1] = 0;
d.mat[0][0]=d.mat[1][0]=1;
A ret=quickP(z-2);//z-2 乘的次数
__int64 ans=(ret.mat[0][0]*y%mod+ret.mat[0][1]*x%mod)%mod;
if(ans < 0)
ans+=mod;
printf("%I64d\n",ans);
}
return 0;
}Codeforces Round #258 (Div. 2) B. Jzzhu and Sequences(矩阵快速幂)
标签:codeforces 矩阵快速幂
原文地址:http://blog.csdn.net/u012860063/article/details/37990519