标签:
http://www.cnblogs.com/AOQNRMGYXLMV/p/4065628.html
一、莫比乌斯(Möbius)函数
对于每个正整数n(n ≥ 2),设它的质因数分解式为:
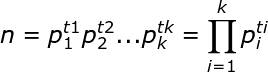
根据这个式子定义n的莫比乌斯函数为:
&space;=\begin{cases}&space;&1\;&space;if&space;\;&space;n=1&space;\\&space;&0&space;\;&space;if&space;\;&space;\exists&space;t_{i}>&space;1&space;\\&space;&(-1)^{k}&space;\;&space;if&space;\;&space;\forall&space;t_{i}=&space;1&space;\end{cases})
也就是如果n有平方因子,则为0. 否则是-1的质因数个数次方。
举个简单的例子:6 = 2 × 3,所以&space;=&space;(-1)^{2}&space;=&space;1) ; 9 = 3×3, 所以
; 9 = 3×3, 所以 &space;=&space;0)
【命题一】
对于正整数n有:
&space;=&space;\begin{cases}&space;1&space;&&space;\text{&space;if&space;}&space;n=1&space;\\&space;0&space;&&space;\text{&space;if&space;}&space;n>&space;1&space;\end{cases})
也就是n>2时,所有n的约数对应函数值之和为0.
证明:
n=1的时候是显然的。
n≥2时:
① 如果d中也含有平方因子,则其值为零。
② 设 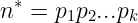 , 若d中不含平方因子,则必有
, 若d中不含平方因子,则必有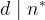 .
.
所以有:&space;=&space;\sum_{d\mid&space;n^{*}}\mu(d)&space;=&space;\sum_{i=0}^{k}\textrm{C}_{k}^{i}&space;(-1)^{i}&space;=&space;(1-1)^{k}&space;=&space;0)
得证。
二、欧拉函数
欧拉函数φ(n)定义为,1~n中与n的最大公约数为1的数字的个数。例如 φ(5) = 4, φ(6) = 2
若p为质数,显然 φ(p) = p-1
若n=pk, 则n的大于1的约数有p, 2p, 3p,...(pk-1-2)p, (pk-1-1)p共pk-1个数。所以φ(n) = pk-pk-1
而且欧拉函数为积性函数(证明较为麻烦,略去),即若m、n互质,有φ(m)φ(n) = φ(mn)
所以对于任意 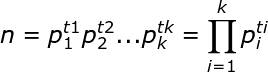
&space;=&space;(p_{1}^{t1}-p_{1}^{t1-1})(p_{2}^{t2}-p_{2}^{t2-1})...(p_{k}^{tk}-p_{k}^{tk-1}))
或者写成这种形式:
&space;=&space;n\prod_{i=1}^{k}(1-&space;\frac{1}{p_{i}}&space;))
莫比乌斯函数和欧拉函数的关系:
}{n}&space;=&space;\sum_{d&space;\mid&space;n}&space;\frac{\mu(d)}{d})
这个不是太难证明,自己在纸上演算一下就明白了。
三、莫比乌斯反演
若定义在正整数集上的两个函数,f(n)和g(n)满足对任意n有:
&space;=&space;\sum_{d&space;\mid&space;n}g(d)) (1)
(1)
则可以通过f来表示g:
&space;=&space;\sum_{d&space;\mid&space;n}\mu&space;(d)f(\frac&space;{n}&space;{d}&space;)) (2)
(2)
反之,亦可以由关系(2)得到(1)
证明:
由式(1)有:
&space;=&space;\sum_{d^{‘}&space;\mid&space;\frac&space;{n}&space;{d}}&space;g(d‘))
于是:
f(\frac&space;{n}&space;{d}&space;)&space;=&space;\sum_{d&space;\mid&space;n}\mu&space;(d)&space;\sum_{d‘&space;\mid&space;\frac&space;{n}{d}&space;}g(d‘))
对于确定的d‘,d将取遍 所有的因子,所以我们可以改变求和顺序:
所有的因子,所以我们可以改变求和顺序:
&space;\sum_{d‘&space;\mid&space;\frac&space;{n}{d}&space;}g(d‘)&space;=&space;\sum_{d‘&space;\mid&space;n}g(d‘)&space;\sum_{d&space;\mid&space;\frac{n}{d‘}&space;}\mu(d))
由上面的推导可知:只有当 即n = d‘时,等式右边才不为0。所以右边和式只剩下g(n)一项了。
即n = d‘时,等式右边才不为0。所以右边和式只剩下g(n)一项了。
简单运用:
上面说到莫比乌斯函数和欧拉函数的关系,}{n}&space;=&space;\sum_{d&space;\mid&space;n}&space;\frac{\mu(d)}{d})
变形为:&space;=&space;\sum_{d&space;\mid&space;n}&space;\mu(d)&space;\frac{n}{d})
视f(n) = n, g(n) = φ(n), 上式相当于反演公式中的(2)式
根据反演公式,可得到(1)式:
)
线性筛选求莫比乌斯反演函数代码。
- void Init()
- {
- memset(vis,0,sizeof(vis));
- mu[1] = 1;
- cnt = 0;
- for(int i=2; i<N; i++)
- {
- if(!vis[i])
- {
- prime[cnt++] = i;
- mu[i] = -1;
- }
- for(int j=0; j<cnt&&i*prime[j]<N; j++)
- {
- vis[i*prime[j]] = 1;
- if(i%prime[j]) mu[i*prime[j]] = -mu[i];
- else
- {
- mu[i*prime[j]] = 0;
- break;
- }
- }
- }
- }
有了上面的知识,现在我们来证明莫比乌斯反演定理。
证明

证明完毕!
嗯,有了莫比乌斯反演,很多问题都可以简化了,接下来我们来看看莫比乌斯反演在数论中如何简化运算的。
题目:http://bz.cdqzoi.com/JudgeOnline/problem.php?id=2818
题意:给一个正整数 ,其中
,其中 ,求使得
,求使得 为质数的
为质数的 的个数,
的个数, 。
。
分析:对于本题,因为是使得 为质数,所以必然要枚举小于等于
为质数,所以必然要枚举小于等于 的质数,那么对于每一个质数
的质数,那么对于每一个质数 ,只
,只
需要求在区间 中,满足有序对
中,满足有序对 互质的对数。
互质的对数。
也就是说,现在问题转化为:在区间 中,存在多少个有序对使得
中,存在多少个有序对使得 互质,这个问题就简单啦,因为
互质,这个问题就简单啦,因为
是有序对,不妨设 ,那么我们如果枚举每一个
,那么我们如果枚举每一个 ,小于
,小于 有多少个
有多少个 与
与 互素,这正是欧拉函数。所以
互素,这正是欧拉函数。所以
我们可以递推法求欧拉函数,将得到的答案乘以2即可,但是这里乘以2后还有漏计算了的,那么有哪些呢?
是 且为素数的情况,再加上就行了。
且为素数的情况,再加上就行了。
代码:
- #include <iostream>
- #include <string.h>
- #include <stdio.h>
- #include <bitset>
-
- using namespace std;
- typedef long long LL;
- const int N = 10000010;
-
- bitset<N> prime;
- LL phi[N];
- LL f[N];
- int p[N];
- int k;
-
- void isprime()
- {
- k = 0;
- prime.set();
- for(int i=2; i<N; i++)
- {
- if(prime[i])
- {
- p[k++] = i;
- for(int j=i+i; j<N; j+=i)
- prime[j] = false;
- }
- }
- }
-
- void Init()
- {
- for(int i=1; i<N; i++) phi[i] = i;
- for(int i=2; i<N; i+=2) phi[i] >>= 1;
- for(int i=3; i<N; i+=2)
- {
- if(phi[i] == i)
- {
- for(int j=i; j<N; j+=i)
- phi[j] = phi[j] - phi[j] / i;
- }
- }
- f[1] = 0;
- for(int i=2;i<N;i++)
- f[i] = f[i-1] + (phi[i]<<1);
- }
-
- LL Solve(int n)
- {
- LL ans = 0;
- for(int i=0; i<k&&p[i]<=n; i++)
- ans += 1 + f[n/p[i]];
- return ans;
- }
-
- int main()
- {
- Init();
- isprime();
- int n;
- scanf("%d",&n);
- printf("%I64d\n",Solve(n));
- return 0;
- }
嗯,上题不算太难,普通的欧拉函数就可以搞定,接下来我们来看看它的升级版。
题意:给定两个数 和
和 ,其中
,其中 ,
, ,求
,求 为质数的
为质数的 有多少对?其中
有多少对?其中 和
和 的范
的范
围是 。
。
分析:本题与上题不同的是 和
和 不一定相同。在这里我们用莫比乌斯反演来解决,文章开头也说了它能大大简化
不一定相同。在这里我们用莫比乌斯反演来解决,文章开头也说了它能大大简化
运算。我们知道莫比乌斯反演的一般描述为:

其实它还有另一种描述,本题也是用到这种。那就是:

好了,到了这里,我们开始进入正题。。。
对于本题,我们设
 为满足
为满足 且
且 和
和 的
的 的对数
的对数
 为满足
为满足 且
且 和
和 的
的 的对数
的对数
那么,很显然 ,反演后得到
,反演后得到
因为题目要求是 为质数,那么我们枚举每一个质数
为质数,那么我们枚举每一个质数 ,然后得到
,然后得到

如果直接这样做肯定TLE,那么我们必须优化。
我们设 ,那么继续得到
,那么继续得到 。
。
到了这里,可以看出如果我们可以先预处理出所有的 对应的
对应的 的值,那么本题就解决了。
的值,那么本题就解决了。
我们设 ,注意这里
,注意这里 为素数,
为素数, 。
。
那么,我们枚举每一个 ,得到
,得到 ,现在分情况讨论:
,现在分情况讨论:
(1)如果 整除
整除 ,那么得到
,那么得到

(2)如果 不整除
不整除 ,那么得到
,那么得到

- #include <iostream>
- #include <string.h>
- #include <stdio.h>
-
- using namespace std;
- typedef long long LL;
- const int N = 10000005;
-
- bool vis[N];
- int p[N];
- int cnt;
- int g[N],u[N],sum[N];
-
- void Init()
- {
- memset(vis,0,sizeof(vis));
- u[1] = 1;
- cnt = 0;
- for(int i=2;i<N;i++)
- {
- if(!vis[i])
- {
- p[cnt++] = i;
- u[i] = -1;
- g[i] = 1;
- }
- for(int j=0;j<cnt&&i*p[j]<N;j++)
- {
- vis[i*p[j]] = 1;
- if(i%p[j])
- {
- u[i*p[j]] = -u[i];
- g[i*p[j]] = u[i] - g[i];
- }
- else
- {
- u[i*p[j]] = 0;
- g[i*p[j]] = u[i];
- break;
- }
- }
- }
- sum[0] = 0;
- for(int i=1;i<N;i++)
- sum[i] = sum[i-1] + g[i];
- }
-
- int main()
- {
- Init();
- int T;
- scanf("%d",&T);
- while(T--)
- {
- LL n,m;
- cin>>n>>m;
- if(n > m) swap(n,m);
- LL ans = 0;
- for(int i=1,last;i<=n;i=last+1)
- {
- last = min(n/(n/i),m/(m/i));
- ans += (n/i)*(m/i)*(sum[last]-sum[i-1]);
- }
- cout<<ans<<endl;
- }
- return 0;
- }
莫比乌斯反演(转)
标签:
原文地址:http://www.cnblogs.com/handsomecui/p/4995231.html
; 9 = 3×3, 所以
所有的因子,所以我们可以改变求和顺序:
即n = d‘时,等式右边才不为0。所以右边和式只剩下g(n)一项了。






















































