UVA11426 GCD - Extreme (II)---欧拉函数的运用

标签：

题目链接：http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&category=473&problem=2421&mosmsg=Submission+received+with+ID+13800900

Given the value of N, you will have to ?nd the value of G. The de?nition of G is given below: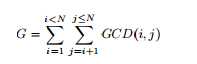

Input
The input ?le contains at most 100 lines of inputs. Each line contains an integer N (1 < N < 4000001).
The meaning of N is given in the problem statement. Input is terminated by a line containing a single
zero.

Output

For each line of input produce one line of output. This line contains the value of G for the correspondingN. The value of G will ?t in a 64-bit signed integer.
　　
Sample Input
10
100
200000
0
Sample Output
67
13015
143295493160

我们假设b[n]表示1到n-1与n的gcd的和，那么G[n]=G[n-1]+b[n];

a[i]表示与gcd（n, x）= i 的x的个数；b[n]=sum( a[i] * i ) , 所以我们只需求a[i]即可；根据gcd(n, x)=i ----->gcd(n/i, x/i) = 1,

因此仅仅要求出欧拉函数phi(n / i)，就能够得到与n / i互质的个数，从而求出gcd(x , n) = i的个数，这样总体就能够求解了

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<algorithm>
using namespace std;

#define N 4000001
typedef long long LL;

LL a[N], b[N], dp[N];

int main()
{
    for(int i=2; i<N; i++)///欧拉打表；
    {
        if(!a[i])
        {
            for(int j=i; j<N; j+=i)
            {
                if(!a[j]) a[j]=j;
                a[j]=a[j]/i*(i-1);
            }
        }
    }

    for(int i=1; i<N; i++)///[1,n-1]中所有的数与n的gcd的和
        for(int j=i*2; j<N; j+=i)
            b[j] += a[j/i]*i;

    for(int i=2; i<N; i++)
        dp[i]=dp[i-1]+b[i];

    int n;
    while(scanf("%d", &n), n)
    {
        printf("%lld\n", dp[n]);
    }
    return 0;
}

View Code

UVA11426 GCD - Extreme (II)---欧拉函数的运用

标签：

原文地址：http://www.cnblogs.com/zhengguiping--9876/p/4998848.html