标签:
4、Median of Two Sorted Arrays
题目
题目要求找到两个排序数组的中位数。
中位数的定义:当n为奇数时,median = array[n/2];当n为偶数时,median = (array[n/2]+array[n/2+1])/2.
暴力算法,两个数组归并排序,对合并的数组求中位数。代码如下:
1 class Solution { 2 public: 3 double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) { 4 vector<int> res; 5 6 int i=0,j=0; 7 int length1 = nums1.size(); 8 int length2 = nums2.size(); 9 10 while (i<length1 && j<length2) 11 { 12 if (nums1[i] < nums2[j]) 13 { 14 res.push_back(nums1[i]); 15 i++; 16 } 17 else 18 { 19 20 res.push_back(nums2[j]); 21 j++; 22 } 23 } 24 while (i<length1) 25 { 26 res.push_back(nums1[i]); 27 i++; 28 } 29 while (j<length2) 30 { 31 res.push_back(nums1[j]); 32 j++; 33 } 34 35 if((length2 + length1) % 2 == 1) 36 return res[(length2 + length1)/2]; 37 else 38 { 39 return (res[(length2 + length1)/2] + res[(length2 + length1)/2 + 1])/2; 40 } 41 42 } 43 };
但是,题目要求时间复杂度为O(log(m+n)),因此上面的算法是不符合要求的,因为其时间复杂度为O(m+n)。
如果时间复杂度为O(log(m+n)),肯定会用到二分查找算法。问题是现在有两个数组,怎样灵活的使用二分查找呢?这就需要开动脑筋 了,如下图的示意图可知
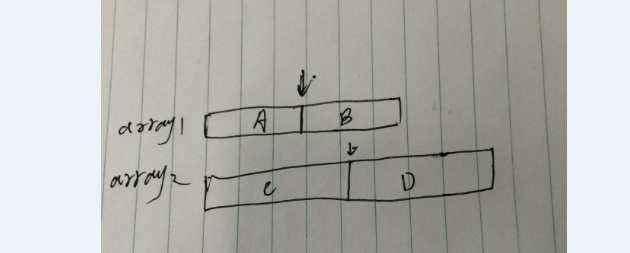
两个数组array1和array2,其中间数(不是中位数)分别为a,b,图中箭头处
如果存在a<b,则一定有A<D,array1和array2的中位数一定是B和C的中位数;
如果a>b,则C<B,array1和array2的中位数一定是A和D的中位数;
标签:
原文地址:http://www.cnblogs.com/LCCRNblog/p/5002618.html