标签:
题目:The Skyline Problem
A city‘s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Now suppose you are given the locations and height of all the buildings as shown on a cityscape photo (Figure A), write a program to output the skyline formed by these buildings collectively (Figure B).
The geometric information of each building is represented by a triplet of integers [Li, Ri, Hi], where Li and Ri are the x coordinates of the left and right edge of the ith building, respectively, and Hi is its height. It is guaranteed that 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX, and Ri - Li > 0. You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.
For instance, the dimensions of all buildings in Figure A are recorded as: [ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] .
The output is a list of "key points" (red dots in Figure B) in the format of [ [x1,y1], [x2, y2], [x3, y3], ... ] that uniquely defines a skyline. A key point is the left endpoint of a horizontal line segment. Note that the last key point, where the rightmost building ends, is merely used to mark the termination of the skyline, and always has zero height. Also, the ground in between any two adjacent buildings should be considered part of the skyline contour.
For instance, the skyline in Figure B should be represented as:[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ].
Notes:
[0, 10000].Li.[...[2 3], [4 5], [7 5], [11 5], [12 7]...] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: [...[2 3], [4 5], [12 7], ...]
中文翻译:输入是一组三元数对,[左边界,右边界,高度],且输入是按左边界由小到大排好序的,输出是一组点[x,y],x是转折的地方,y是转折后的坐标。通过这几个关键点就可以刻画出天际线。
这条题目的难点在于当出现一座新的建筑物的时候要考虑的情况很多。首先要列出所有可能的情况。
我们注意到当加入一个新的[Li,Ri,h]时,它不会对x<Li的点产生影响,也不会对y>h的点产生影响。同时,由于输入的时候Li是从小到大排好序的,所以易得若某个点(x0,y0) 使得y0>h,则对于所有x<=x0的点(即(x0,y0)左侧的点)都不会受到影响。
所以我们先从后往前找到当前天际线中第一个大于等于新建筑物高度的点或者在建筑物左侧的点P,再分三种情况讨论:
情况一:P点纵坐标等于建筑物高度。如图
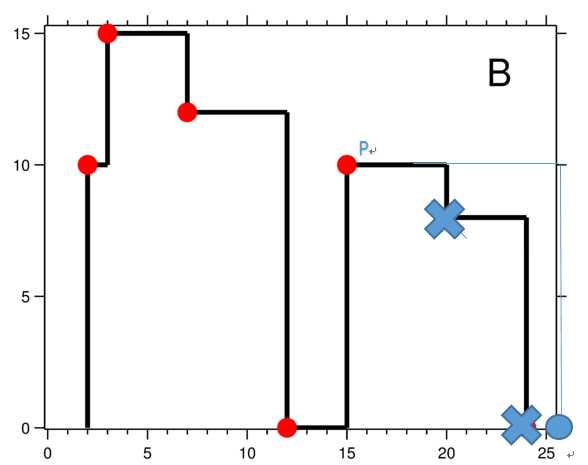
情况二:P点纵坐标小于建筑物高度。
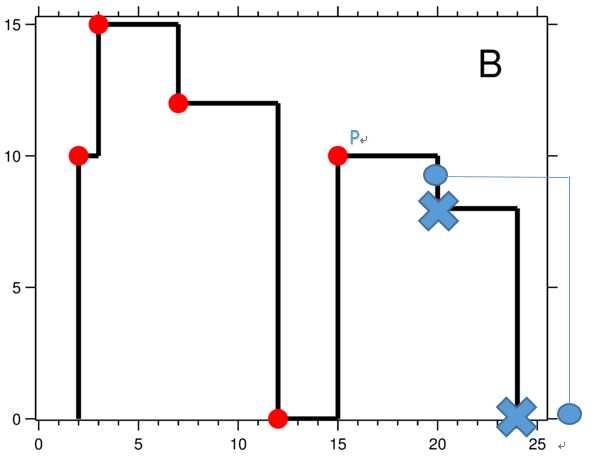
情况三:P点纵坐标小于建筑物高度。
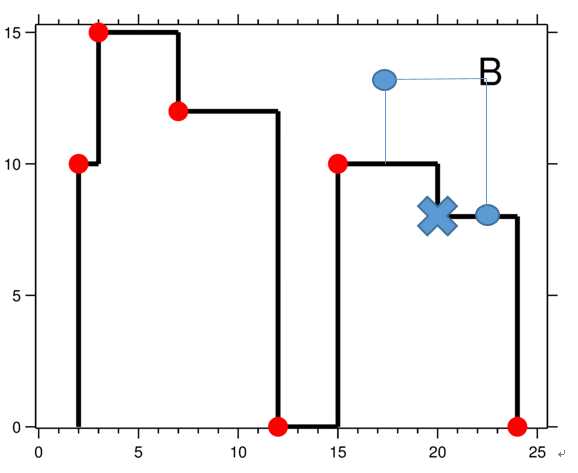
源代码
class Solution { public: vector<pair<int, int>> getSkyline(vector<vector<int>>& buildings) { //初始化 pair<int,int> first(0,0); vector<pair<int,int>> result; result.push_back(first); vector<vector<int>>::iterator buildings_it;//遍历所有建筑物的指针 for (buildings_it=buildings.begin();buildings_it!=buildings.end();buildings_it++) { //从后往前找到当前天际线中第一个超过当前建筑物高度的点或者在建筑物左侧的点 vector<pair<int,int>>::iterator result_it; for (result_it=result.end();result_it!=result.begin();) { result_it--; if (result_it->second>=(*buildings_it)[2]||result_it->first<(*buildings_it)[0]) break; } //如果建筑物的左轮廓被遮挡 if (result_it->second==(*buildings_it)[2]) { vector<pair<int,int>>::iterator it=result_it+1; //如果右轮廓也被遮挡,不做改变 //否则删掉被右轮廓遮挡的点 if (it->first<(*buildings_it)[1]) { //it->second=(*buildings_it)[2]; pair<int,int> pre=*it; for (;it!=result.end()&&it->first<=(*buildings_it)[1];) { pre=*it; it=result.erase(it); } //插入右轮廓的点 pair<int,int> q((*buildings_it)[1],pre.second); result.insert(it,q); } } else if (result_it->second>(*buildings_it)[2]) { vector<pair<int,int>>::iterator it=result_it+1; //如果右轮廓也被遮挡,不做改变 //否则删掉被右轮廓遮挡的点 if (it->first<(*buildings_it)[1]) { pair<int,int> pre=*it; it->second=(*buildings_it)[2]; for (it++;it!=result.end()&&it->first<=(*buildings_it)[1];) { pre=*it; it=result.erase(it); } //插入右轮廓的点 pair<int,int> q((*buildings_it)[1],pre.second); result.insert(it,q); } } //如果左轮廓没有被遮挡 else { //添加新点 pair<int,int> pre=*result_it; vector<pair<int,int>>::iterator it=result_it+1; pair<int,int> q((*buildings_it)[0],(*buildings_it)[2]); it=result.insert(it,q); //删掉被遮挡的点 for (it++;it!=result.end()&&it->first<=(*buildings_it)[1];) { pre=*it; it=result.erase(it); } //插入右轮廓的点 pair<int,int> p((*buildings_it)[1],pre.second); result.insert(it,p); } } result.erase(result.begin()); return result; } };
语法方面需要注意vector类的erase和insert两个函数都会返回一个iterator,
因此,在遍历容器的所有元素过程中通过erase删除一个元素或者通过insert插入一个元素后,要将返回值赋给迭代变量,否则会出现"vector iterators incompatible"的错误。
运行结果
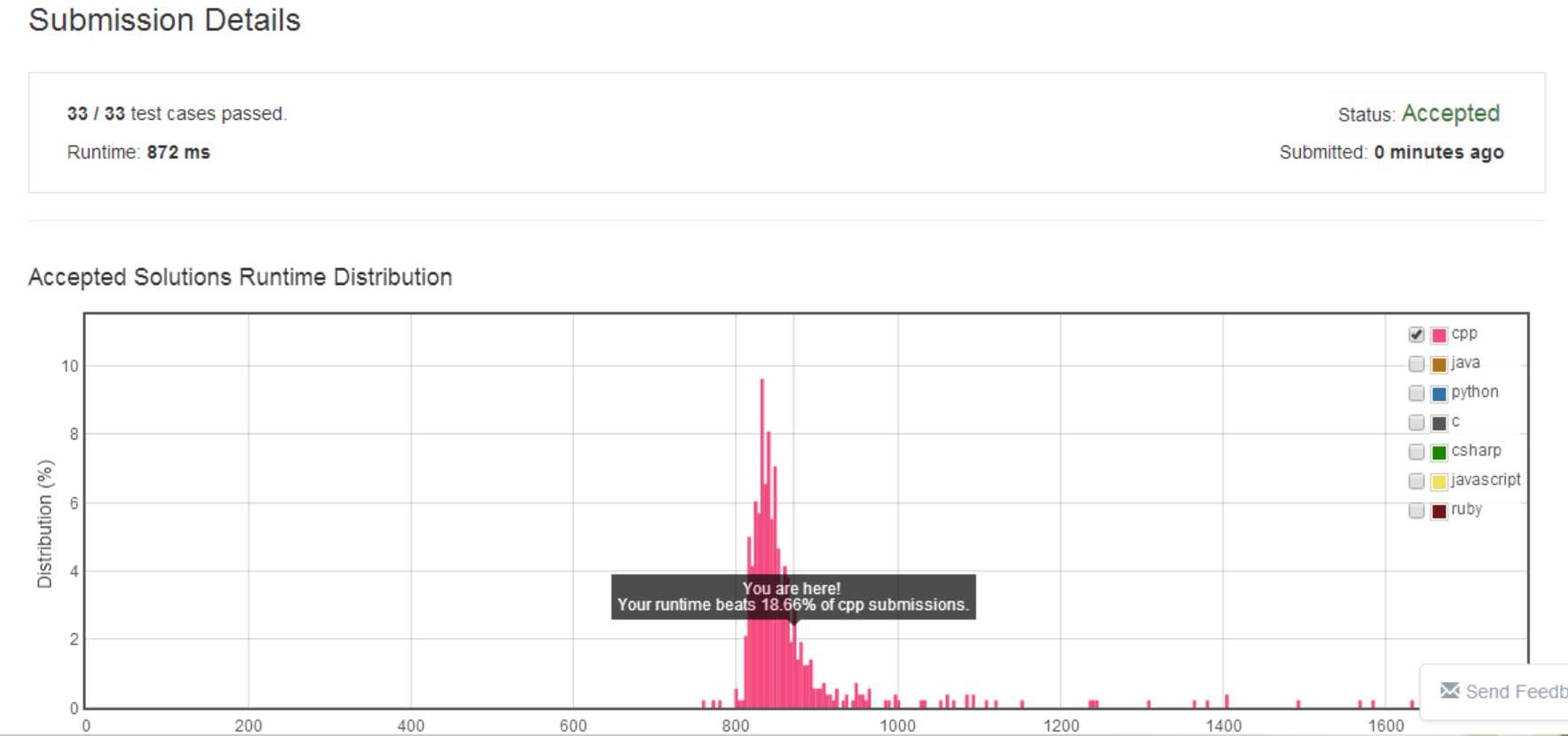
用时较长,仍需改进。
标签:
原文地址:http://www.cnblogs.com/zizhao/p/5003939.html