Coursera 机器学习笔记（七）

标签：

主要为第九周内容：异常检测、推荐系统

（一）异常检测(DENSITY ESTIMATION)

核密度估计（kernel density estimation）是在概率论中用来估计未知的密度函数，属于非参数检验方法之一。密度估计是指给定数据集 x(1),x(2),..,x(m)，我们假使数据集是正常的，我们希望知道新的数据 x(test)是不是异常的，即这个测试数据不属于该组数据的几率如何。我们所构建的模型应该能根据该测试数据的位置告诉我们其属于一组数据的可能性 p(x)。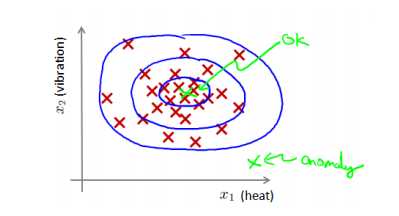

通过密度估计之后，选择一个概率阈值进行判断是否是异常，这也是异常检测中常用的方法。如：

1. 高斯分布

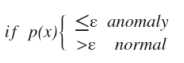
   高斯核函数是核密度估计中常用的核函数。其中一元高斯概率密度函数为：

   

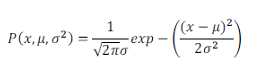
   可以利用已有的数据来预测总体中的μ和σ2的计算方法如下：

   

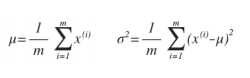
   多元高斯分布的概率密度函数为：

   

   

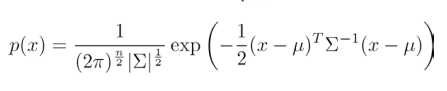
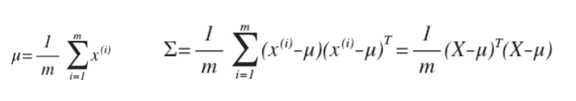
   注：机器学习中对于方差我们通常只除以 m 而非统计学中的（m-1）。

2. 异常检测

   一般的高斯分布模型中，对于给定的数据集 x(1),x(2),...,x(m) ，我们要针对每一个特征计算μ和σ2的估计值，根据模型计算 p(x)：

   

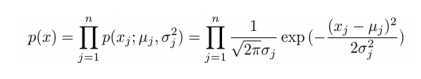
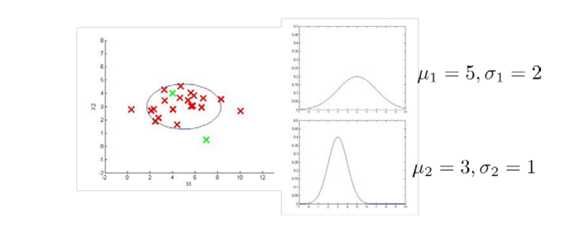
   如下图所示：

   

   对于多元高斯分布模型，首先计算所有特征的平均值，然后再计算协方差矩阵，最后我们计算多元高斯分布的 p(x)：

   

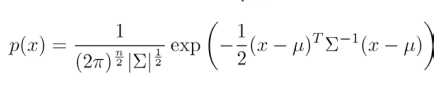
（二）推荐系统

基于内容

基于用户

http://www.ccf.org.cn/resources/1190201776262/2010/05/12/h049617016.pdf

Coursera 机器学习笔记（七）

标签：

原文地址：http://www.cnblogs.com/findwg/p/5006322.html