标签:
1 #include <iostream> 2 #include <string> 3 #include <Eigen/Dense> 4 #include "math.h" 5 #include <stdlib.h> 6 7 #define pi 3.141592653589793 8 9 using namespace std; 10 using namespace Eigen; 11 12 int Dimension = 2; 13 14 MatrixXd & getCoordinate(MatrixXd &,string & coordinate);//将输入坐标值的字符串转换为数值 15 MatrixXd & RotationMatrix(MatrixXd &,string &); //根据输入的旋转角度求得旋转矩阵 16 MatrixXd & Move(MatrixXd &,MatrixXd &); //平移之后得到平移坐标矩阵 17 MatrixXd & Rotate(MatrixXd &,MatrixXd &,string &,string &); //旋转结果 18 MatrixXd & LineMirror(MatrixXd &, Vector3d &); 19 20 int main() 21 { 22 int NumberOfPoints ; 23 string GraphicName; 24 string Coordinate; 25 26 cout <<"输入图形名字,图形点数,点的坐标:" <<endl; 27 cin >> GraphicName >> NumberOfPoints >> Coordinate; 28 29 MatrixXd PointMatrix(Dimension,NumberOfPoints); //定义点的矩阵 30 PointMatrix = getCoordinate(PointMatrix,Coordinate); 31 MatrixXd store = PointMatrix; 32 33 cout << "初始坐标值" << endl << PointMatrix << endl; 34 35 string Command; 36 string GraphicNameC; 37 string RotPoint; //旋转中心 38 string CommandCoordinate; //旋转点坐标 39 40 cout <<"请输入指令,如move l1 (3,6),rotate -30 (0,0):" <<endl; 41 cin >> Command >> GraphicNameC >> CommandCoordinate>>RotPoint ; 42 43 if (Command == "move") 44 { 45 MatrixXd MoveMatrix(Dimension,1); //定义移动矩阵 46 //int Num = 1; 47 MoveMatrix = getCoordinate(MoveMatrix,CommandCoordinate); 48 PointMatrix = Move(PointMatrix,MoveMatrix); 49 50 } 51 if(Command == "rotate") 52 { 53 MatrixXd Rotation(Dimension,Dimension); //旋转矩阵 54 PointMatrix = Rotate(PointMatrix,Rotation,CommandCoordinate,RotPoint); 55 } 56 57 cout << "The transfer result is:" <<endl << PointMatrix << endl; 58 59 double a,b,c; 60 cout << "请输入直线的参数a,b,c,ax+by+c=0:"<< endl; 61 cin >> a >> b >> c; 62 Vector3d LCo(a,b,c); 63 MatrixXd MirrorResult; 64 MirrorResult = LineMirror(store,LCo); 65 cout << "关于直线镜像的结果:"<< endl << MirrorResult<< endl; 66 system("pause"); 67 } 68 69 MatrixXd & getCoordinate(MatrixXd & pointMatrix,string & coordinate) 70 { 71 //提取输入的坐标值 72 string tempt; //temp用来存储字符串里面的数字量 73 int count = 0; 74 // MatrixXd pointMatrix(Dimen,pointNumber); 75 for(int i = 0; i < coordinate.length(); i++) 76 { 77 if((coordinate[i] >= ‘0‘ && coordinate[i] <= ‘9‘)|| 78 coordinate[i] == ‘,‘||coordinate[i] == ‘)‘|| coordinate[i] == ‘.‘) 79 { 80 if(coordinate[i] == ‘,‘ || coordinate[i] == ‘)‘) 81 { 82 count = count + 1; 83 int k = count/2; 84 int m = count%2 - 1; 85 if(m == 0) 86 double j = pointMatrix(0,k) = atof(tempt.c_str()); 87 if(m == -1) 88 { 89 double n = 0; 90 n = pointMatrix(1,k-1) = atof(tempt.c_str()); 91 int i = 0; 92 } 93 tempt.clear(); 94 continue; 95 } 96 tempt = tempt + coordinate[i]; 97 } 98 } 99 return pointMatrix; 100 } 101 102 //根据输入的转换角度求出转换矩阵 103 MatrixXd & RotationMatrix(MatrixXd & Rotation,string & arc) 104 { 105 double angle = atof(arc.c_str()); 106 107 double s1,c1; 108 s1 = sin(angle*pi/180); 109 c1 = cos(angle*pi/180); 110 111 if(abs(s1)<0.000000000000001) 112 s1 = 0.0; 113 if (abs(c1) < 0.000000000000001) 114 c1=0; 115 116 Rotation(0,0) = c1; 117 Rotation(0,1) = s1; 118 Rotation(1,0) = -s1; 119 Rotation(1,1) = c1; 120 121 return Rotation; 122 } 123 124 //求移动后的点坐标 125 MatrixXd & Move(MatrixXd & point,MatrixXd & moveMatrix) 126 { 127 int Num = point.cols(); 128 129 for(int i = 0; i < Num; i++) 130 { 131 point(0,i) = point(0,i) + moveMatrix(0,0); 132 point(1,i) = point(1,i) + moveMatrix(1,0); 133 } 134 135 return point; 136 } 137 138 //求旋转后的点坐标 139 MatrixXd & Rotate(MatrixXd & Poi,MatrixXd & Rot ,string &command,string &RPoint) 140 { 141 MatrixXd rotPoint; //存储输入旋转中心 142 MatrixXd temp(Dimension,Dimension); 143 144 rotPoint = getCoordinate(temp,RPoint); //旋转中心坐标 145 rotPoint = (-1)*rotPoint; 146 Poi = Move(Poi,rotPoint); //旋转中心移动到原点 147 Rot = RotationMatrix(Rot,command); 148 Poi = Rot*Poi; //关于原点对称 149 rotPoint = (-1)*rotPoint; 150 Poi = Move(Poi,rotPoint); //将旋转中心移回原始位置 151 152 return Poi; 153 } 154 155 //求镜像后的坐标值 156 MatrixXd & LineMirror(MatrixXd & point,Vector3d & Co) 157 { 158 int Num = point.cols(); 159 double a = Co(0); 160 if( Co(0) == 0) 161 { 162 double y=-Co(2)/Co(1); 163 for(int i = 0; i < Num; i++) 164 point(1,i) = 2*y - point(1,i); 165 } 166 if(Co(1) == 0) 167 { 168 double x = -Co(2)/Co(0); 169 for(int i = 0; i < Num; i++) 170 point(0,i) = 2*x - point(0,i); 171 } 172 if(Co(0)!=0 && Co(1)!=0) 173 { 174 175 for(int i = 0; i < Num; i++) 176 { 177 double L = (Co(0)*point(0,i)+Co(1)*point(1,i)+Co(2)); 178 double D = (Co(0)*Co(0)+Co(1)*Co(1)); 179 if(Co(0)*point(0,i)+Co(1)*point(1,i)+Co(2) == 0) 180 continue; 181 point(0,i) = point(0,i)-2*Co(0)*L/D; 182 point(1,i) = point(1,i)-2*Co(1)*L/D; 183 } 184 } 185 return point; 186 }
//执行结果
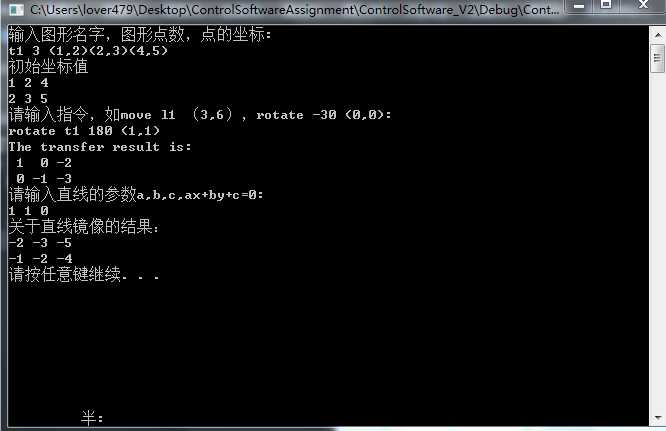
该程序目前为止只实现了平面上任意点数对任意旋转中心的旋转和平移和对于一条任意直线的镜像,三维的旋转还在努力中。。。。
标签:
原文地址:http://www.cnblogs.com/RXWein/p/5008797.html