标签:
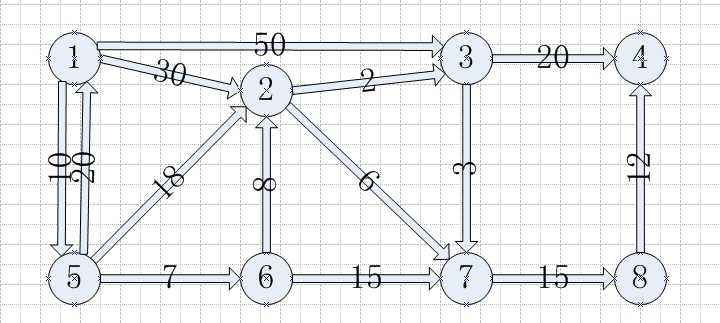
从单个顶点到其余各顶点之间的最短路径:
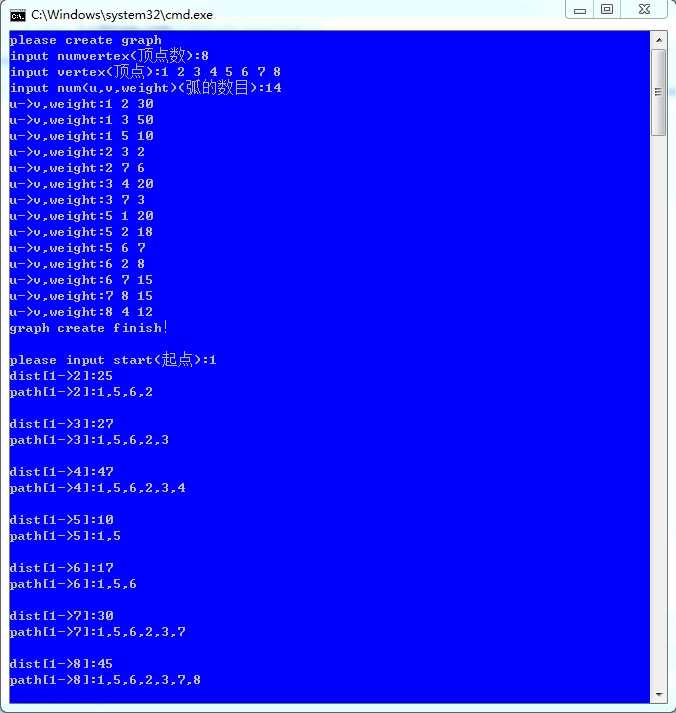
1 #include "iostream" 2 #include "vector" 3 #include "stack" 4 using namespace std; 5 6 const int MaxNumVertex = 20; //最大顶点数 7 const int infinity = 65535;//无穷大 8 typedef int elementtype; //elementtype 为int 型 9 class graph{ 10 public: 11 graph(); 12 ~graph(); 13 elementtype insertvertex(elementtype v); //在图中增加一个顶点 14 elementtype insertedge(elementtype v,elementtype u,elementtype weight);//在图中增加一条从v顶点到u顶点的弧 15 elementtype firstadj(elementtype v);//求图g中顶点v的第一个邻接点 16 elementtype nextadj(elementtype v,elementtype m);//求图中顶点v的m邻接点之后的邻接点 17 elementtype Dijkstra(elementtype v0);//求解从v0到各顶点的最短路径 18 elementtype create();//创建图 19 int CurrentVertex;//当前顶点数 20 21 private: 22 elementtype vertex[MaxNumVertex];//顶点表 23 elementtype edge[MaxNumVertex][MaxNumVertex];//图中弧的类型 24 25 }; 26 27 /* 28 *初始化 29 */ 30 graph::graph() 31 { 32 CurrentVertex = 0; 33 int i,j; 34 for (i=MaxNumVertex-1;i>=1;i--) 35 { 36 for (j=MaxNumVertex-1;j>=1;j--) 37 { 38 edge[i][j] = infinity; 39 40 } 41 } 42 43 } 44 45 /* 46 *在图中增加一个顶点 47 */ 48 elementtype graph::insertvertex(elementtype v) 49 { 50 //判断这个顶点是否已经存在 51 int i; 52 bool flags = true; 53 for(i=1; i<=CurrentVertex; i++) 54 { 55 if(vertex[i]==v) 56 { 57 flags = false; 58 break; 59 } 60 } 61 62 if(flags) 63 { 64 CurrentVertex++; 65 vertex[CurrentVertex] = v; 66 }else{ 67 cout<<v<<"顶点已经存在!"<<endl; 68 } 69 return 0; 70 } 71 72 /* 73 *在图中增加一条从v顶点到u顶点的弧 74 */ 75 elementtype graph::insertedge(elementtype v,elementtype u,elementtype weight) 76 { 77 if(edge[v][u]!=infinity) 78 { 79 cout<<v<<"->"<<u<<"这条弧弧已经存在!"<<endl; 80 }else{ 81 edge[v][u] = weight; 82 } 83 return 0; 84 } 85 86 87 /* 88 *求图中顶点v的第一个邻接点 89 */ 90 elementtype graph::firstadj(elementtype v) 91 { 92 int u,i; 93 bool flags = true;//用于判断是否存在邻接点 94 for(i=1;i<=CurrentVertex;i++) 95 { 96 if(edge[v][i]!=0){ 97 u = i; 98 flags = false; 99 break; 100 } 101 } 102 if(flags) u = 0;//邻接点不存在 103 return u; 104 } 105 106 /* 107 *求图中顶点v的m邻接点以后的邻接点 108 */ 109 elementtype graph::nextadj(elementtype v,elementtype m) 110 { 111 int i,u; 112 bool flags = true; 113 for(i=m+1;i<=CurrentVertex;i++) 114 { 115 if(edge[v][i]!=0) 116 { 117 u = i; 118 flags = false; 119 break; 120 } 121 } 122 if(flags) u = 0;//邻接点不存在 123 return u; 124 } 125 126 /* 127 *求解v0到各顶点的最短路径 128 */ 129 elementtype graph::Dijkstra(elementtype v0) 130 { 131 int i,j,k,w,v; 132 bool solved[20]; 133 int dist[20]; 134 vector<vector<int>>path(MaxNumVertex);//存储v0到各顶点的路径 135 for(i=1;i<=CurrentVertex;i++) 136 { 137 solved[i] = false; 138 } 139 140 solved[v0] = true;//将v0设置为已解顶点 141 for(i=1;i<=CurrentVertex;i++) 142 { 143 if(edge[v0][i]!=infinity) 144 { 145 dist[i] = edge[v0][i]; 146 path[i].push_back(v0); 147 path[i].push_back(i); 148 }else{ 149 dist[i] = infinity; 150 } 151 } 152 153 for(i=1;i<CurrentVertex;i++) 154 { 155 int min = infinity; 156 for(j=1;j<=CurrentVertex;j++)//在未解顶点中搜索最近的顶点v 157 { 158 if((solved[j]==false)&&(dist[j]<min)) 159 { 160 min = dist[j]; 161 v = j; 162 } 163 } 164 165 solved[v] = true;//所搜索到的当前最短的未解顶点为已解顶点 166 for(w=firstadj(v);w!=0;w=nextadj(v,w))//修改v的后继路径以及长度 167 { 168 if(dist[v]+edge[v][w]<dist[w]) 169 { 170 dist[w] = dist[v]+edge[v][w];//修改w的dist值 171 path[w].clear();//清空w的path 172 //重新形成w的path 173 for(k=0;k<path[v].size();k++) 174 { 175 path[w].push_back(path[v][k]); 176 } 177 path[w].push_back(w); 178 } 179 } 180 } 181 for(i=1;i<=CurrentVertex;i++) 182 { 183 if(v0!=i) 184 { 185 cout<<"dist["<<v0<<"->"<<i<<"]:"<<dist[i]<<endl; 186 cout<<"path["<<v0<<"->"<<i<<"]:"; 187 for(j=0;j<path[i].size();j++) 188 { 189 if(j<path[i].size()-1)cout<<path[i][j]<<","; 190 else cout<<path[i][j]<<endl; 191 } 192 cout<<endl; 193 } 194 } 195 return 0; 196 } 197 /* 198 *创建图 199 */ 200 elementtype graph::create() 201 { 202 int i,numv,v,u,weight; 203 cout<<"please create graph"<<endl; 204 cout<<"input numvertex(顶点数):"; 205 cin>>numv; 206 cout<<"input vertex(顶点):"; 207 for(i=1;i<=numv;i++) 208 { 209 cin>>v; 210 insertvertex(v); 211 } 212 cout<<"input num(u,v,weight)(弧的数目):"; 213 cin>>numv; 214 for(i=1;i<=numv;i++) 215 { 216 cout<<"u->v,weight:"; 217 cin>>u>>v>>weight; 218 insertedge(u,v,weight); 219 } 220 cout<<"graph create finish!"<<endl<<endl; 221 return 0; 222 } 223 graph::~graph() 224 { 225 } 226 227 int main() 228 { 229 graph g; 230 g.create(); 231 int v0; 232 cout<<"please input start(起点):"; 233 cin>>v0; 234 g.Dijkstra(v0); 235 return 0; 236 }
标签:
原文地址:http://www.cnblogs.com/minmsy/p/5013682.html