标签:
在一个NxN的棋盘上,每个格子里有若干个棋子,假设起点为左上角的格子,且每次只能向下或向右走一格,问怎样走才能得到最多的棋子。
这是很简单的递推题了。
因为只能向下或者向右,所以其实我们可以把棋盘看成一颗这样的树(以N=3为例)
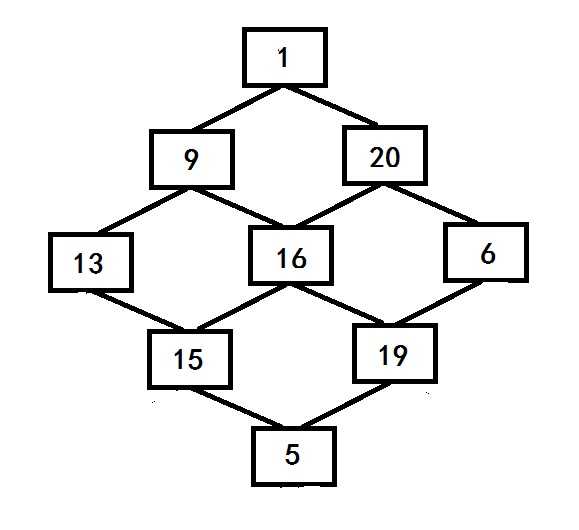
起点最上,终点最下,数字即为棋子,只能向下走,要找一条数字总和最大的路线。
这个问题怎么考虑呢,我们可以从头开始推,然后记录起始点到其他所有点的最大值。
先保存第一行到第二行的最大值 再保存第三行,这时中间的有两条路,选择最大那条即可
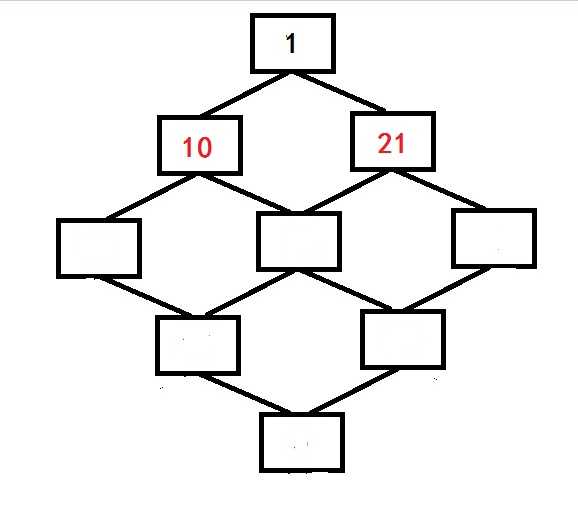
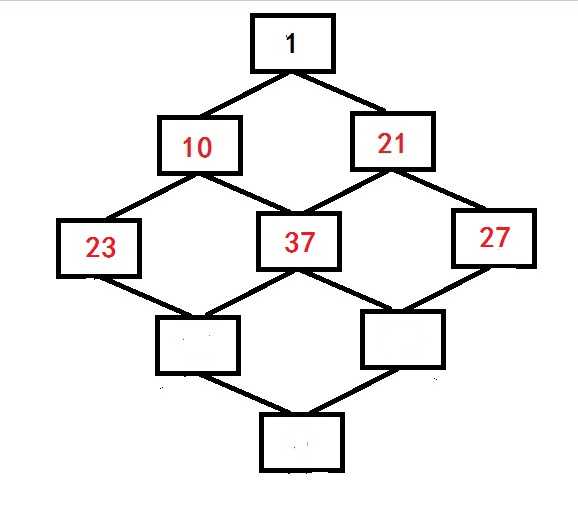
由此就可得到起始点到任意点的最大距离
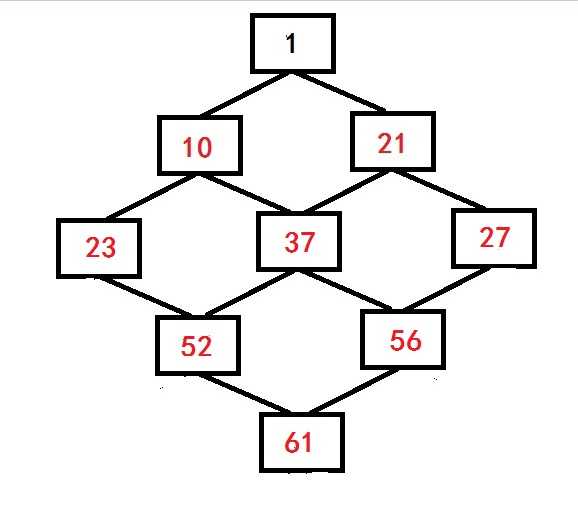
由此我们可以知道,从下往上,每个点都是选择上面连接的两个点中,距离最大的那个,然后加上自身的值。
设map[n][n]保存棋盘每个点的棋子数,dp[n][n]保存起始点到每个点的最大距离
即有状态转移方程:
dp[i][j] = dp[i][j-1] + dp[i-1][j] + map[i][j]
#include <iostream> #include <string> #include <cstring> #include <cstdlib> #include <cstdio> #include <cmath> #include <algorithm> #include <stack> using namespace std; #define MEM(a,b) memset(a,b,sizeof(a)) #define pf printf #define sf scanf #define debug printf("!/m") #define INF 1000 #define MAX(a,b) a>b?a:b #define blank pf("\n") #define LL long long LL dp[INF][INF]; LL map[INF][INF]; typedef pair<int,int> pa; stack<pair<int,int> > road; int main() { int n,i,j; MEM(map,0); MEM(dp,0);; pf("请输入棋盘的维度n\n"); sf("%d",&n); pf("请输入棋盘每个格子里的棋子数\n"); for(i = 1;i<=n;i++) { for(j = 1;j<=n;j++) { sf("%lld",&map[i][j]); } } for(i = 1;i<=n;i++) { for(j = 1;j<=n;j++) { dp[i][j] = max(dp[i-1][j],dp[i][j-1]) + map[i][j]; } } road.push(make_pair(n,n)); int a=n,b=n; for(;;) { if(dp[a][b-1] >= dp[a-1][b]) b = b-1; else a = a-1; if(a==0 || b==0) break; road.push(make_pair(a,b)); } pf("起始点到每个点的最大距离如下\n"); for(i = 1;i<=n;i++) { for(j = 1;j<=n;j++) { pf("%lld\t",dp[i][j]); } blank; } pf("得到的最多的棋子为%lld\n",dp[n][n]); pf("路径如下:\n"); while(!road.empty()) { pa x= road.top(); road.pop(); pf("(%d,%d) ",x.first,x.second); } blank; return 0; } /* 3 1 20 6 9 16 19 13 15 5 */
标签:
原文地址:http://www.cnblogs.com/qlky/p/5023881.html