标签:
| Time Limit: 2000MS | Memory Limit: 65536K | |||
| Total Submissions: 16444 | Accepted: 8035 | Special Judge | ||
Description
Input
Output
Sample Input
1 103000509 002109400 000704000 300502006 060000050 700803004 000401000 009205800 804000107
Sample Output
143628579 572139468 986754231 391542786 468917352 725863914 237481695 619275843 854396127
Source
题意:每行每列每个小的九宫格 每个数字只出现一次;
看着很高大上的题目做起来这么好玩,搜索真是很神奇!应该是第一次写带有返回值的搜索
转载请注明出处:優YoU http://user.qzone.qq.com/289065406/blog/1303713313
大致题意:
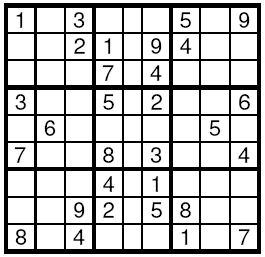
九宫格问题,也有人叫数独问题
把一个9行9列的网格,再细分为9个3*3的子网格,要求每行、每列、每个子网格内都只能使用一次1~9中的一个数字,即每行、每列、每个子网格内都不允许出现相同的数字。
0是待填位置,其他均为已填入的数字。
要求填完九宫格并输出(如果有多种结果,则只需输出其中一种)
如果给定的九宫格无法按要求填出来,则输出原来所输入的未填的九宫格
解题思路:
DFS试探,失败则回溯
用三个数组进行标记每行、每列、每个子网格已用的数字,用于剪枝
bool row[10][10]; //row[i][x] 标记在第i行中数字x是否出现了
bool col[10][10]; //col[j][y] 标记在第j列中数字y是否出现了
bool grid[10][10]; //grid[k][x] 标记在第k个3*3子格中数字z是否出现了
row 和 col的标记比较好处理,关键是找出grid子网格的序号与 行i列j的关系
即要知道第i行j列的数字是属于哪个子网格的
首先我们假设子网格的序号如下编排:
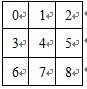
由于1<=i、j<=9,我们有: (其中“/”是C++中对整数的除法)
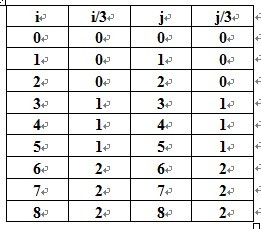
令a= i/3 , b= j/3 ,根据九宫格的 行列 与 子网格 的 关系,我们有:
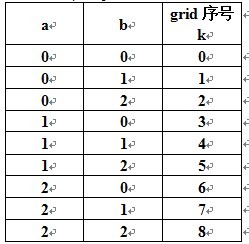
不难发现 3a+b=k
即 3*(i/3)+j/3=k
又我在程序中使用的数组下标为 1~9,grid编号也为1~9
因此上面的关系式可变形为 3*((i-1)/3)+(j-1)/3+1=k
有了这个推导的关系式,问题的处理就变得非常简单了,直接DFS即可

1 #include <iostream> 2 #include <cstring> 3 #include <algorithm> 4 #include <cstdio> 5 6 using namespace std; 7 int row[10][10],col[10][10],grid[10][10]; 8 int g[15][15]; 9 bool dfs(int x,int y) 10 { 11 if(x == 10) 12 { 13 return true; 14 } 15 bool flag = false; 16 if(g[x][y]) 17 { 18 if(y == 9) 19 { 20 flag = dfs(x + 1, 1); 21 } 22 else 23 { 24 flag = dfs(x, y + 1); 25 } 26 if(flag) 27 return true; 28 else 29 return false; 30 } 31 else if(g[x][y] == 0) 32 { 33 for(int i = 1; i <= 9; i++) 34 { 35 int k = (x - 1) / 3 * 3 + (y - 1) / 3 + 1; 36 if(col[y][i] == 0 && row[x][i] == 0 && grid[k][i] == 0) 37 { 38 g[x][y] = i; 39 col[y][i] = 1; 40 row[x][i] = 1; 41 grid[k][i] = 1; 42 if(y < 9) 43 { 44 flag = dfs(x,y + 1); 45 } 46 else 47 { 48 flag = dfs(x + 1, 1); 49 } 50 if(flag == false) 51 { 52 g[x][y] = 0; 53 col[y][i] = 0; 54 row[x][i] = 0; 55 grid[k][i] = 0; 56 } 57 else 58 return true; 59 } 60 } 61 } 62 return false; 63 } 64 int main() 65 { 66 int t; 67 scanf("%d", &t); 68 getchar(); 69 while(t--) 70 { 71 memset(row,0,sizeof(row)); 72 memset(col,0,sizeof(col)); 73 memset(grid,0,sizeof(grid)); 74 memset(g,0,sizeof(g)); 75 char ch; 76 for(int i = 1; i <= 9; i++) 77 { 78 for(int j = 1; j <= 9; j++) 79 { 80 scanf("%c", &ch); 81 if(ch != ‘0‘) 82 { 83 g[i][j] = ch - ‘0‘; 84 row[i][ch - ‘0‘] = 1; 85 col[j][ch - ‘0‘] = 1; 86 int k = (i - 1) / 3 * 3 + (j - 1) / 3 + 1; 87 grid[k][ch - ‘0‘] = 1; 88 } 89 } 90 getchar(); 91 } 92 dfs(1,1); 93 for(int i = 1; i <= 9; i ++) 94 { 95 for(int j = 1; j <= 9; j++) 96 { 97 printf("%d",g[i][j]); 98 } 99 printf("\n"); 100 } 101 } 102 return 0; 103 }
标签:
原文地址:http://www.cnblogs.com/zhaopAC/p/5024240.html