标签:
传递要查找的数组,数组大小以及要查找的值,返回该值在数组中的索引
int find1(int *a, int n,int key) { assert(a); int *end = a + n, *beg = a; for (; beg < end; ++beg) if (*beg == key) return beg-a
; return -1; }
如果查找每个元素的概率都相等,那么平均比较次数为
1/n*(1+2+3+4+...+n)=(1/n)*n*(n+1)/2=(n+1)/2
但是实际过程中并非查找每个元素的概率都相等。举个例子,一个数组中存储着1 2 3 4 5 6 7 8 9 10这10个数,我们几乎总是查找8和9,而几乎不查找1,2,3,4。那么是不是把8,9放在数组前面,1,2,3,4放在数组后面更合理?
那么,在查找的时候,将查找到的元素key向前移动OFFSET个位置,这样,对key查找的越频繁,key的位置越靠前。而不经常要查找的元素,则被挤到了数组后面。
int find2(int *a, int n, int key) { assert(a); int *end = a + n, *beg = a; int tmp; int i; for (; beg < end;++beg) if (*beg == key) { if (beg-a < OFFSET) { tmp = *a; *a = *beg; *beg = tmp; } else { tmp = *beg; *beg = *(beg - OFFSET); *(beg - OFFSET) = tmp; } return beg-a; } return -1; }
测试程序
#include<stdio.h> #include<time.h> #include<stdlib.h> #include<assert.h> #define OFFSET 400 #define ARRAY_SIZE 100000 int main() { int a[ARRAY_SIZE]; int i; double begTime, endTime; srand((unsigned)time(NULL)); for (i = 0; i < ARRAY_SIZE; ++i) a[i] = rand() % 10000; //[0,9999] printf("生成数组完毕\n"); //测试1 begTime = clock(); i = 100000; while (i--) find1(a, ARRAY_SIZE, rand() % 11000); endTime = clock(); printf("find1用时%lfs\n", (endTime - begTime) / CLOCKS_PER_SEC); //测试2 begTime = clock(); i = 100000; while (i--) find2(a, ARRAY_SIZE, rand() % 11000); endTime = clock(); printf("find2用时%lfs\n", (endTime - begTime) / CLOCKS_PER_SEC); //测试3 begTime = clock(); i = 100000; while (i--) find2(a, ARRAY_SIZE, rand() % 1000); endTime = clock(); printf("find2用时%lfs\n", (endTime - begTime) / CLOCKS_PER_SEC); system("pause"); return 0; }
测试结果:
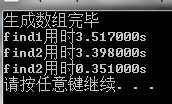
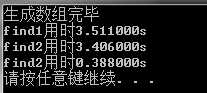
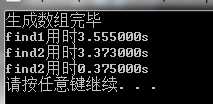
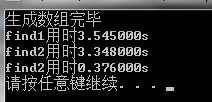
分析:
测试1和测试2的表明find2比find1要快一点。然而我个人觉得,应该是find2比find1慢一点,可能是rand()%11000产生的随机数并非等概率随机数。
测试2改变了原数组a,但是因为数组a本来就是随机的,测试2对数组a的改变也是随机的,而测试3的查找也是随机的,随意测试2对数组a的改变并不影响测试3
测试3产生的随机数是0到1000之间,用来模拟不等概率查找。
标签:
原文地址:http://www.cnblogs.com/inori/p/5025759.html