标签:
这次题目挺有意思的,可惜D题差几分钟没交对。E题的博弈还是很基础的SG函数,让我复习了下博弈。
基本的输入输出,一个公式输出来即可,但是要注意的是,写之前先化简变成全为整数的情况。

#include <iostream> #include <stdio.h> using namespace std; int m[10],w[10]; int main(int argc, const char * argv[]) { for(int i=0;i<5;i++) cin>>m[i]; for(int i=0;i<5;i++) cin>>w[i]; int hs,hu; cin>>hs>>hu; int ans; ans=0; for(int i=0;i<5;i++) { ans += max(150*(i+1),(i+1)*(500-2*m[i])-50*w[i]); } ans+=100*hs; ans-=hu*50; cout<<ans; return 0; }
这题其实还是要想想的,比赛的时候想了下加猜了下。
给一个递增序列长度为n,然后有k个箱子,每个箱子最多只能放两个数。最后求箱子里面最大的不超过多少。
1.箱子肯定尽量全部用上。
2.如果n>k的话,则有n-k个箱子放两个数,2*k-n个箱子放一个数,则把最大2*k-n个数单个放入箱子中
3.剩下来的2*(n-k)个小的数,按一大一小的选择方式放入箱子中。(为什么呢? 其实仔细想想肯定是这样贪心的,顺序只要变了结果不可能会变小)
需要注意的是:第2步中最大的肯定为整个序列最大的一个数,第3步最大的必须一个一个枚举。

#include <iostream> #include <stdio.h> using namespace std; int g[100100]; int main(int argc, const char * argv[]) { int n,k; cin>>n>>k; for(int i=1;i<=n;i++) cin>>g[i]; if(k>=n) cout<<g[n]; else { int tn=2*(n-k); int ans=max(g[n],g[1]+g[tn]); for(int i=1;i<=(n-k);i++) ans=max(ans,g[i]+g[tn+1-i]); cout<<ans; } return 0; }
这题基本上就在考智商吧,感觉聪明人瞬间就可以看到解法了,我等菜B推了快半小时才看出来。。。
首先,有一个很重要的性质,对于一段0,1序列,翻转后的01间断个数不变。
比如0111001011,等价于010101,翻转后变为101010,间断个数不变。
第二个重要性质,一次翻转最多只能加2
然后就是最关键的:我把00,11这样连续相同的段且长度=2的叫做连段。比如0011101中00,11(靠左)和11(靠右)就是连段,
如果序列中出现了两个以上的连段. 如xxx00yyy11xxx,只需要变成xxx01y‘y’y‘01xxx,有之前说的性质1,yyy的间断个数不变,所以整体就加2
如果序列中只有一个连段,那么只能加1
如果没有连段,那么序列就是0和1相间,只能加0
这样只需要O(n)统计一遍连段的个数即可。

#include <iostream> #include <stdio.h> using namespace std; char g[100100]; int main(int argc, const char * argv[]) { int n; cin>>n; scanf("%s",g); int ans=1; char pre=g[0]; for(int i=1;i<n;i++) { if(g[i]!=pre) { ans++; pre=g[i]; } } //然后看有没有三个的 int flag3=0; for(int i=0;i<n-2;i++) { if(g[i]==g[i+1]&&g[i+1]==g[i+2]) { flag3=1; break; } } if(flag3==1) { printf("%d",ans+2); } else { int flag2=0; for(int i=0;i<n-1;i++) { if(g[i]==g[i+1]) flag2++; } if(flag2>=2) printf("%d",ans+2); else { if(flag2==1) printf("%d",ans+1); else printf("%d\n",ans); } } return 0; }
这题一开始我还以为用到了数论和组合数学的知识,其实好像用到了一点置换的概念,但是还是一个推理就能解出来的题目。

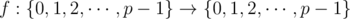
观察这个函数。
1.如果k=0,那么f(0)=0,只有这个信息,然后f(1),f(2),...,f(p-1)都可以随便选,结果就是p^(p-1)
2.k!=0时
设有一个x1,则f(kx1 mod p) = k*f(x1) mod p
设x2=x1*k%p,则f(kx2 mod p) = k*f(x2) mod p
...
设xs=xs-1*k%p,且xs=x1 (因为一定会有循环结)
f(x1) = ks*f(x1) mod p
因为p是素数,如果ks mod p=1,则f(x1)可以为任意选,也就是有p种可能
如果 ks mod p != 1,f(x1)只能为0,也就是只有一种可能。
这样一来,对于在一个循环结内的数就能知道有多少可能。把所有循环结的情况相乘就是最后的答案了。

#include <iostream> #include <stdio.h> using namespace std; #define MOD 1000000007 int g[1001000]; int mark[1001000]; int main(int argc, const char * argv[]) { int p,k; cin>>p>>k; if(k==0) { long long ans=1; for(int i=1;i<p;i++) ans=ans*p%MOD; cout<<ans; return 0; } for(int i=0;i<p;i++) { g[i] = ((long long)i*k)%p; } long long ans=1; for(int i=0;i<p;i++) { if(mark[i]) continue; mark[i]=1; long long tmp=1; int ti = g[i]; while(ti!=i) { mark[ti]=1; tmp++; ti=g[ti]; } long long tk=1; for(int j=0;j<tmp;j++) tk=(tk*k)%p; if(tk==1) ans=ans*p%MOD; else ans*=1; } cout<<ans; return 0; }
我在开始想这题的时候,忘了sg函数,想凭找规律找到结果。 结果我想多了,对于一半的情况是可以找规律的,但是另一半我是始终没找出来,我想如果聪明人应该还是可以通过规律做出这题。通过这题我也知道挂不得区域赛什么的,博弈题很少,因为博弈题套路固定,而且基本上就那几种特殊的博弈。巴什,威佐夫,nim。难的估计太难大家又不会了。o(╯□╰)o
像我一样,忘记sg函数的或者还不会的可以看这里:博弈SG函数
Codeforces Round #334 (Div. 2)
标签:
原文地址:http://www.cnblogs.com/chenhuan001/p/5032004.html