标签:
给出2*n + 1 个的数字,除其中一个数字之外其他每个数字均出现两次,找到这个数字。
链接:http://www.lintcode.com/zh-cn/problem/single-number/
给出 [1,2,2,1,3,4,3],返回 4
一次遍历,常数级的额外空间复杂度
方法1思路:将所有的数转换成二进制,因为是int类型,共32位。申请常数级(32位)的额外空间,然后每个数对应的位相加,最后对应位上的和模2。最后的结果就是单个数对应的二进制数。
class Solution { public: /** * @param A: Array of integers. * return: The single number. */ int singleNumber(vector<int> &A) { // write your code here int ans[35]; memset(ans, 0, sizeof(ans)); for(int i=0; i<A.size(); ++i){ for(int k=0; k<32; k++) ans[k] = (ans[k]+((A[i]>>k)&1))%2; } int ret = 0; int base = 1; for(int i=0; i<32; ++i){ ret += ans[i]*base; base *= 2; } return ret; } };
方法2思路:通过异或,相同的数结果为0,那么最后的结果一定是落单的数字。
class Solution { public: /** * @param A: Array of integers. * return: The single number. */ int singleNumber(vector<int> &A) { // write your code here int ans = 0; for(int i=0; i<A.size(); ++i) ans ^= A[i]; return ans; } };
给出3*n + 1 个的数字,除其中一个数字之外其他每个数字均出现三次,找到这个数字。
链接:http://www.lintcode.com/zh-cn/problem/single-number-ii/
给出 [1,1,2,3,3,3,2,2,4,1] ,返回 4
一次遍历,常数级的额外空间复杂度
同上一题的方法1一样的思路。
class Solution { public: /** * @param A : An integer array * @return : An integer */ int singleNumberII(vector<int> &A) { // write your code here int ans[35]; memset(ans, 0, sizeof(ans)); for(int i=0; i<A.size(); ++i){ for(int k=0; k<32; k++) ans[k] = (ans[k]+((A[i]>>k)&1))%3; } int ret = 0; int base = 1; for(int i=0; i<32; ++i){ ret += ans[i]*base; base *= 2; } return ret; } };
给出2*n + 2个的数字,除其中两个数字之外其他每个数字均出现两次,找到这两个数字。
链接:http://www.lintcode.com/zh-cn/problem/single-number-iii/
给出 [1,2,2,3,4,4,5,3],返回 1和5
O(n)时间复杂度,O(1)的额外空间复杂度
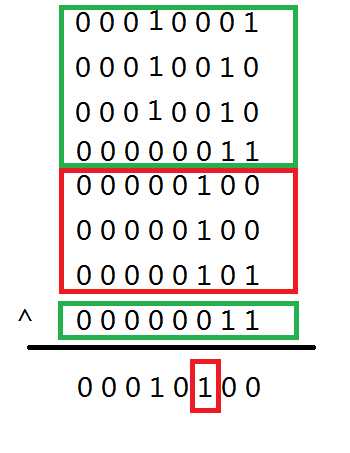
如上图所示,所有数的异或的结果等于两个落单数异或的结果(设为S)。如何根据这个异或的结果将落单的数找出来呢?首先,S的值一定不为0,那么找到S对应的二进制数值为1的位(找到任意一个位为1都行, 这里我们找到S的二进制最后一个为1的位,设为P),根据这一个位置,将所有的数划分成两部分,一部分是对应二进制P位是1,另一部分对应二进制P位是0。这样就把两个落单的数划分到了不同的集合里去了。如上图的红色框集合和绿色框集合。然后就转换成“2*m+1个数字,除了一个数字其他数字均出现两次”的问题,也就是题目1:落单的数I。
class Solution { public: /** * @param A : An integer array * @return : Two integers */ int findNum(int k, vector<int> &A, bool flag){ int ret = 0; for(int i=0; i<A.size(); ++i){ if(flag && (1<<k)&A[i]) ret ^= A[i]; if(!flag && !((1<<k)&A[i])) ret ^= A[i]; } return ret; } vector<int> singleNumberIII(vector<int> &A) { // write your code here int x = 0; for(int i=0; i<A.size(); ++i) x ^= A[i]; int k = 0; for(k; k<32; ++k)//找到异或值最后一个1,说明该位置P之后,两个不同的数对应的二进制是相同的 if((1<<k)&x) break; //根据这个位置P,转换成“2*m+1个数字,除了一个数字其他数字均出现两次”的问题 //将位置P上对应为1的数字异或得到一个数字,然后再将位置P上对应为0的数字异或得到一个数字,最后得到答案 vector<int> ans; ans.push_back(findNum(k, A, true)); ans.push_back(findNum(k, A, false)); return ans; } };
标签:
原文地址:http://www.cnblogs.com/hujunzheng/p/5045084.html