标签:
曾经觉得能写很长的代码就是厉害的表现,随着学习的深入,对于好的代码有了更加深刻的认识,一个好的代码应该:
1、可读性。好的代码不仅能让机器读懂,更要让看代码的人读懂----合理布局,逻辑清晰。
2、充分发挥语言的优势,比如接下来的matlab矩阵化编程。
3、占用尽可能小的内存,运行尽量快,输出结果尽量容易处理。并在此之间找到平衡。
。。。。。
需要说明的是,如果没有对复杂网络有基本的了解,下面的东西没有看下去的必要。关于小世界网络和无标度网络,可以参考Watts DJ和Strogatz SH的Collective dynamics of ‘small-world‘ networks(NATURE)以及Barabasi AL和Albert R的 Emergence of scaling in random networks(SCIENCE)。
之前,国庆期间曾经用了四百行代码(C语言)实现了无标度网络,之后又用一到两百行代码写完了小世界网络。现在看这些代码,确实受制于C语言语法的限制,所以写出来十分冗杂,而且不易理解。由于最近在学习matlab编程,所以尝试了一下,两个代码加起来竟然不到一百行。而且没有使用matlabBGL之类的工具。而且算法上由于语言变的更加自由,所以算法上也优化了不少(由后面的度分度图就可以看出来)
此外,虽然matlab基于JVM,但是只要算法设计的好,还是可以完爆之前的C语言,关于无标度网络的博客中提到计算1000个节点需要35min,经过测试,这个matlab程序处理10000个节点的时间是38min,1000个节点是21.9s!新的程序时间复杂度O(N^2),N是节点数量(由于数据结构没有时间系统学习,时间复杂度可能说错了!)。
最后,matlab可以对矩阵进行稀疏化处理,而无标度网络正是一个极其稀疏的网络,所以,借助稀疏化操作,使得matlab也能操作较大的矩阵。
先贴上实现小世界网络的matlab代码:
1 NodesNum = 1000; 2 K = 10; 3 p = 1; 4 A = sparse(NodesNum, NodesNum); 5 for i=1:K/2 6 A = A + diag(ones(1, length(diag(A, i))), i); 7 end 8 A = sparse(A); 9 for i=1:K/2 10 A(i, (NodesNum-K/2+i):NodesNum) = 1; 11 end 12 A = A + A‘; 13 for i=1:K/2 14 P = rand(1,NodesNum); 15 P = find(P <= p); 16 for j=1:length(P) 17 while true 18 x = fix(rand()*NodesNum)+1; 19 if A(x, P(j)) == 0 20 A(x, P(j)) = 1; 21 A(P(j), x) = 1; 22 break; 23 end 24 end 25 26 if P(j) <= NodesNum-i 27 A(NodesNum-i, P(j)) = 0; 28 A(P(j), NodesNum-i) = 0; 29 else 30 A(P(j)-NodesNum+i, P(j)) = 0; 31 A(P(j), P(j)-NodesNum+i) = 0; 32 end 33 34 end 35 end 36 clear i j P x 37 B3 =A^3; 38 B33 = B3(1:NodesNum+1:end); 39 B2 = A^2; 40 B22 = B2(1:NodesNum+1:end); 41 c = B33./(B22.*(B22-1)); 42 c(isnan(c)) = 0; 43 C = mean(c); 44 clear B33 B3 B2 B22 45 46 Paths = graphallshortestpaths(tril(A), ‘directed‘, false); 47 Paths = tril(Paths); 48 L = sum(sum(Paths)) / nchoosek(NodesNum, 2);
再贴上无标度网络实现的matlab代码
1 tic 2 m0 = 10; 3 m = 5; 4 NodesNum = 1000; 5 A = sparse(NodesNum, NodesNum); 6 A(1:m0,1:m0) = round(rand(m0)); 7 A = tril(A); 8 A = A+A‘; 9 A = A - diag(diag(A)); 10 for i=m0+1:NodesNum 11 Degree = sum(A(1:i-1,1:i-1)); 12 for j=2:i-1 13 Degree(j) = Degree(j) + Degree(j-1); 14 end 15 LinksNum = 0; 16 while LinksNum<m 17 link = fix(rand()*Degree(i-1)+1); 18 for j=1:i-2 19 if link<=Degree(1) && A(i,1)==0 20 A(i,1) = 1; 21 A(1,i) = 1; 22 LinksNum = LinksNum+1; 23 elseif link>Degree(j) && link<=Degree(j+1) && A(i,j+1)==0 24 A(i,j+1) = 1; A(j+1,i) = 1; 25 LinksNum = LinksNum+1; 26 end 27 end 28 end 29 end 30 Degree = sum(A); 31 list = unique(Degree); 32 num = zeros(1,length(list)); 33 for i=1:length(list) 34 num(i) = length(find(list(i)==Degree)); 35 end 36 toc 37 loglog(list,num,‘.‘,‘markersize‘,20) 38 xlabel(‘k‘),ylabel(‘P(k)‘)
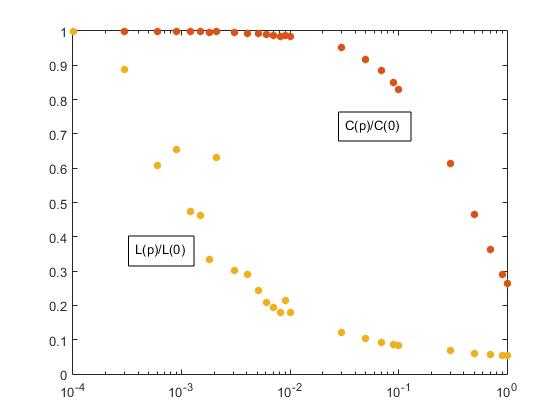
再贴一张小世界网络聚类系数和最短平均路径变化图(最短路径变化有点波动,看来算法还需优化)
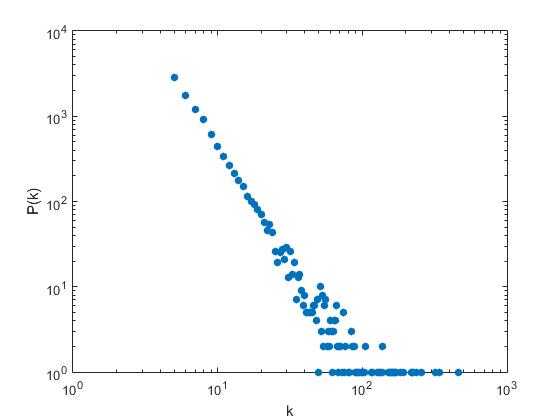
最后贴一张10000节点生成的matlab度分布对数坐标图,确实比之前的明显多了(算法改进立竿见影):
2015-12-14
标签:
原文地址:http://www.cnblogs.com/zhaoyu1995/p/5046858.html