标签:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
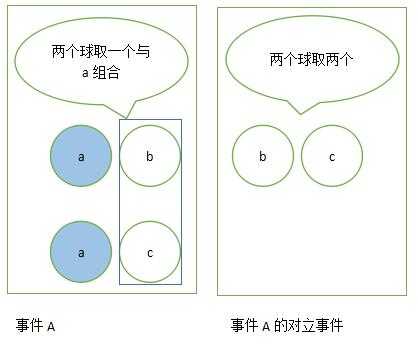
//在n个球中,任取m个(不放回),求有多少种取法#include <stdio.h>int fun(int n, int m) { if(n<m) return 0; if(n==m) return 1; if(m>0) return fun(n-1, m-1) + fun(n-1, m);}int main(void){ printf("%d\n", fun(3, 2)); return 0;}/*=======================2015年12月15日22:28:40高中的排列组合中有这个公式的n中取m = n-1中取m-1 + n-1中取m如何理解呢?n中取m个,在这些组合中 (比如abc取两个球,在这些组合中ab ac bc中)可以分解成两种事件,约定有一个特殊球 (约定为a球)1.取特殊球的所有组合 即可以把特殊球理解成标签一样,撕掉 特殊球消失 不含有特殊球 就是总球n-1,取m-1个 分别与a球组合 (b c中取1个构成ab, ac)2.不取特殊球的所有组合 即这些组合不含有特殊球 总球n-1,取m个球 (bc中取两个构成bc)2是1的对立事件这样分解问题逐层递归就可以解决这个问题了。 |
标签:
原文地址:http://www.cnblogs.com/startnow/p/5049850.html