解:
中文
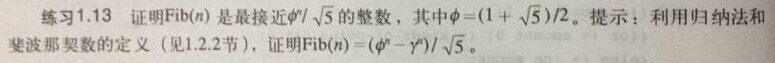
原版

麻蛋的垃圾中文翻译,艹
先证明提示中的:
Fib(0)成立,Fib(1)成立,Fib(2)成立,假设Fib(n)成立,则(那两个拉丁字母用x y分别代替):
x=(1+sqrt(5))/2, y=(1-sqrt(5))/2
Fib(n+1)=Fib(n)+Fib(n-1)=...=((x+1)*pow(x,n-1)-(y+1)*pow(y,n-1))/sqrt(5)
因为x+1=pow(x,2), y+1=pow(y,2)
所以Fib(n+1)=(pow(x,n+1)-pow(y,n+1))/sqrt(5)
所以有Fib(n)=(pow(x,n)-pow(y,n))/sqrt(5)成立
再证明题目中的:
Fib(n)-pow(x,n)/sqrt(5)=(pow(x,n)-pow(y,n))/sqrt(5)-pow(x,n)/sqrt(5)=-pow(y,n)/sqrt(5)
当n为奇数时,Fib(n)>pow(x,n)/sqrt(5),于是
(pow(x,n)/sqrt(5)-(Fib(n)-1)) - (Fib(n)-pow(x,n)/sqrt(5)) >0
同理,当n为偶数时,Fib(n)<pow(x,n)/sqrt(5),于是
((Fib(n)+1)-pow(x,n)/sqrt(5)) - (pow(x,n)/sqrt(5)-Fib(n)) > 0
所以Fib(n)是最接近pow(x,n)/sqrt(5)的整数。
原文地址:http://my.oschina.net/u/1445655/blog/293636