标签:
除去NARF这种和特征检测联系比较紧密的方法外,一般来说特征检测都会对曲率变化比较剧烈的点更敏感。Harris算法是图像检测识别算法中非常重要的一个算法,其对物体姿态变化鲁棒性好,对旋转不敏感,可以很好的检测出物体的角点。甚至对于标定算法而言,HARRIS角点检测是使之能成功进行的基础。
HARRIS算法的思想还是很有意思的。很聪明也很trick.
其思想及数学推导大致如下:
1.在图像中取一个窗 w (矩形窗,高斯窗,XX窗,各种窗,某师姐要改标定算法不就可以从选Harris的窗开始做起么。。。。。)
2.获得在该窗下的灰度 I
3.移动该窗,则灰度会发生变化,平坦区域灰度变化不大,边缘区域沿边缘方向灰度变化剧烈,角点处各个方向灰度变化均剧烈
4.依据3中条件选出角点
当然啦,如果Harris算子的实现也和它的思想这么平淡那我就不表扬他聪明了,Harris算子的具体实现方法,利用的是图像偏微分方程的思想。
先给出抽象数学表达式(不要问我为什么这么淡,我也不知道):
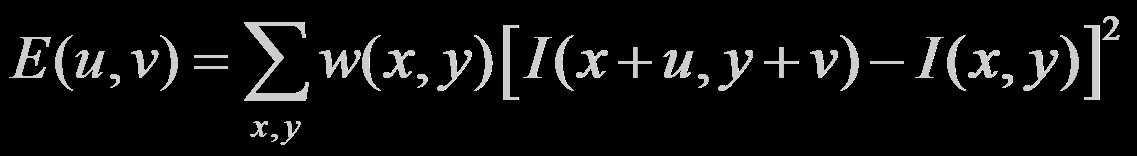
其中 w 代表窗函数,某个x,y为图像坐标,u,v是一个移动向量(既反应移动方向,也反应移动大小)。
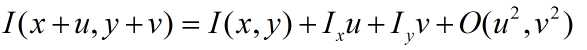
Ix表示图像沿x方向的差分,Iy表示图像沿y方向的差分。图像差分算子有什么Sober~PXX~总之很多就对了,一阶差分还是很好求的。
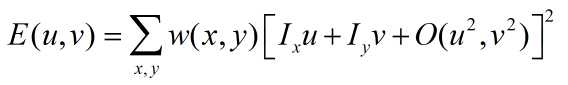
显然,E(u,v)可以用另外一种形式来表示了。最终可以表达为协方差矩阵的形式。
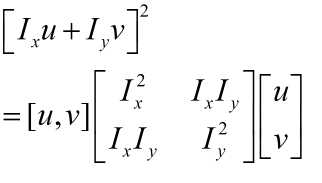
OK,在这里我们有了数学中最优雅的表达——Matrix,especially symmetric Matrix. Nothing is better than that.
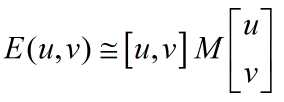
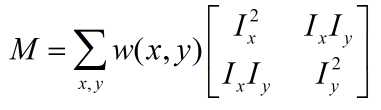
显然,E(u,v)的值和u,v有关。。。很有关。。
1.可以取一组u,v,让E(u,v)的值最小。
2.还可以取一组u,v,让E(u,v)的值最大。
这些u,v怎么取,显然就和矩阵M的方向有关了。OK,让我们换一个思路来看这个矩阵。
平面内的一个矩阵乘以一个向量v,大概简单的写成 Mv
它会使得这个向量发生一个作用:旋转,拉伸,平移.....总之,这种作用叫做 线性变换
矩阵的左边好像也是一个向量,只不过是横着写的([u v]),换而言之,那就是 vT(v的转置)。
vT(Mv)......这是啥?
意思好像是。。。。v先旋转+拉伸一下,然后再在它自己身上投影,最终的 E(u,v)本质上来说,就是这个投影的长度。。。嗯,对,投影的长度
好了。我们现在明确了 E(u,v) 的数学几何意义,再回过头来想想,要怎样才能让这个投影的长度达到最大或者最小呢?
显然,答案就是矩阵的特征值与特征向量,当[u v]T 取特征向量方向的时候,矩阵M只有拉伸作用,而没有旋转作用,这时的投影长度是最长的(如果反向投则是负的最长)。
到此为止,我们已经知道了 E(u,v)的最大和最小值了(笨办法是求出特征向量方向再带进去,聪明的方法是直接看矩阵特征值,特征值就是放大倍数)。并且,分析可以知道,特征值越大,那么说明 E(u,v)越大。
1.两个特征值都很大==========>角点(两个响应方向)
2.一个特征值很大,一个很小=====>边缘(只有一个响应方向)
3.两个特征值都小============>平原地区(响应都很微弱)
基于上述特征,有很多人设计了角点的快速判据。
有 det(M) - trace(M)^2
有 det(M)/trace(M)
.....等等很多,但是这不重要,思想都是一样的。(某师姐这里又有一个标定算法的创新点哦。。。。我会告诉你换换判据又是个新思路?)
在2DHarris里,我们使用了 图像梯度构成的 协方差矩阵。 图像梯度。。。嗯。。。。每个像素点都有一个梯度,在一阶信息量的情况下描述了两个相邻像素的关系。显然这个思想可以轻易的移植到点云上来。每个点都有个法线方向,法线方向就是梯度方向。
去森林公园看母猴子了,明天继续写
标签:
原文地址:http://www.cnblogs.com/ironstark/p/5064848.html