标签:
通常是二元分类器(也可以用于多元分类),例如以下的分类问题
假设 (Hypothesis):$$h_\theta(x) = g(\theta^Tx)$$ $$g(z) = \frac{1}{1+e^{-z}}$$ 其中g(z)称为sigmoid函数,其函数图象如下图所示,可以看出预测值$y$的取值范围是(0, 1),这样对于 $h_\theta(x) \geq 0.5$, 模型输出 $y = 1$; 否则如果 $h_\theta(x) < 0.5$, 模型输出 $y = 0$。
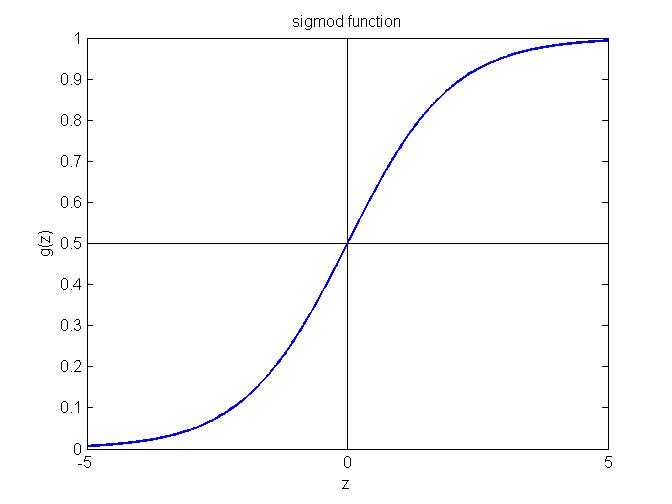
$h_\theta(x)$=该数据属于 $y=1$分类的概率, 即 $$h_\theta(x) = P\{y = 1|(x; \theta)\}$$ 此外由于y只能取0或者1两个值,换句话说,一个数据要么属于0分类要么属于1分类,假设已经知道了属于1分类的概率是p,那么当然其属于0分类的概率则为1-p,这样我们有以下结论 $$P(y=1|x;\theta) + P(y=0|x;\theta) = 1$$ $$P(y=0|x;\theta) = 1 - P(y = 1|x; \theta)$$
函数$g(z)$是单调函数,
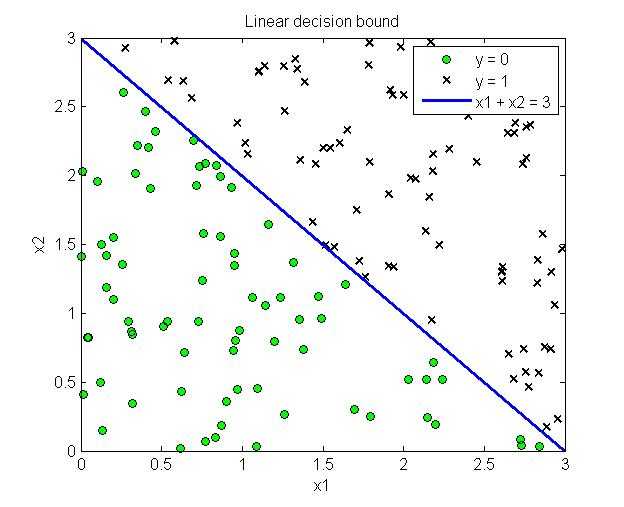
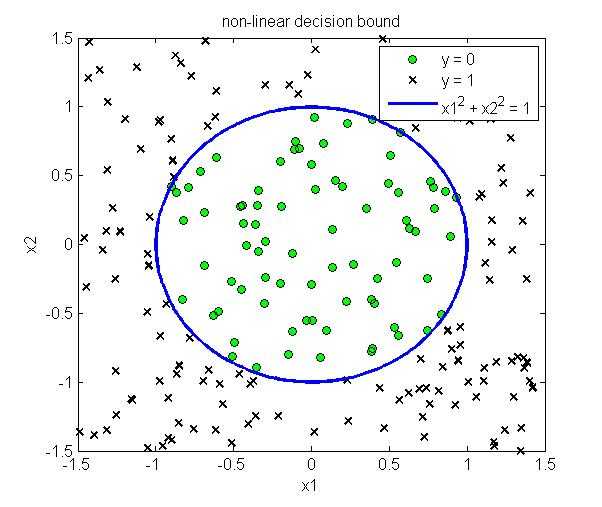
这样不需要具体的带入sigmoid函数,只需要求解$\theta^Tx \geq 0$即可以得到对应的分类边界。下图给出了线性分类边界和非线性分类边界的例子
在线性回归中我们定义的代价函数是,即采用最小二乘法来进行拟合
$$J(\theta)=\frac{1}{m}\sum\limits_{i=1}^{m}\text{cost}(h_\theta(x^{(i)}), y)$$ $$\text{cost}(h_\theta(x), y)=\frac{1}{2}(h_\theta(x)-y)^2$$
然而由于这里的假设是sigmoid函数,如果直接采用上面的代价函数,那么$J(\theta)$将会是非凸函数,无法用梯度下降法求解最小值,因此我们定义Logistic cost function为
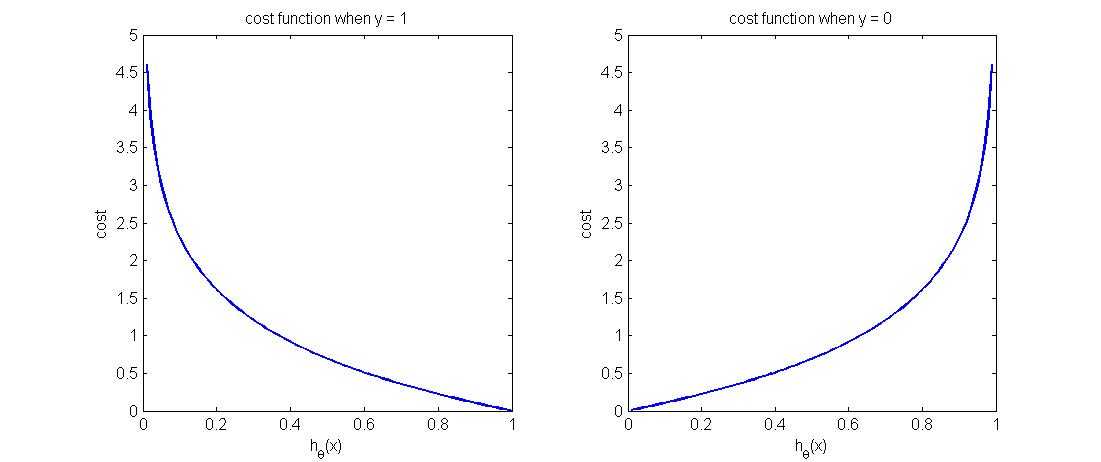
$$\text{cost}(h_\theta(x), y)=\begin{cases}-log(h_\theta(x)); y = 1\\ -log(1-h_\theta(x)); y = 0\end{cases}$$
函数图像如下图所示,可以看到,当$y=1$时,预测正确时($h_\theta(x)=1$)代价为零,反之预测错误时($h_\theta(x)=0$)的代价非常大,符合我们的预期。同理从右图可以看出,当y=0时,预测正确时($h_\theta(x)=0$)代价函数为0,反之预测错误时($h_\theta(x)=1$)代价则非常大。表明该代价函数定义的非常合理。
前面的代价函数是分段函数,为了使得计算起来更加方便,可以将分段函数写成一个函数的形式,即
$$\text{cost}(h_\theta(x), y)=-y\log(h_\theta(x))-(1-y)\log(1-h_\theta(x))$$
$$J(\theta)=-\frac{1}{m}\sum\limits_{i=1}{m}y^{(i)}\log(h_\theta(x^{(i)})) + (1-y^{(i)})\log(1-h_\theta(x^{(i)}))$$
有了代价函数,问题转化成一个求最小值的优化问题,可以用梯度下降法进行求解,参数$\theta$的更新公式为
$$\theta_j = \theta_j - \alpha \frac{\partial}{\partial \theta_j}J(\theta)$$
其中对$J(\theta)$的偏导数为 $$\frac{\partial}{\partial \theta_j}J(\theta) = \frac{1}{m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$$ 注意在logistic回归中,我们的假设函数$h_\theta(x)$变了(加入了sigmoid函数),代价函数$J(\theta)$也变了(取负对数,而不是最小二乘法), 但是从上面的结果可以看出偏导数的结果完全和线性归回一模一样。那么参数$\theta$的更新公式也一样,如下
$$\theta_j = \theta_j - \alpha \frac{1}{m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$$
为什么偏导数长这样子,为什么和线性回归中的公式一模一样?公开课中没有给出证明过程,主要是多次使用复合函数的链式求导法则,具体的证明过程可以看这里。
除了梯度下降算法,可以采用高级优化算法,比如下面的集中,这些算法优点是不需要手动选择$\alpha$,比梯度下降算法更快;缺点是算法更加复杂。
Logistic回归可以用于多元分类,采用所谓的One-vs-All方法,具体来说,假设有K个分类{1,2,3,...,K},我们首先训练一个LR模型将数据分为属于1类的和不属于1类的,接着训练第二个LR模型,将数据分为属于2类的和不属于2类的,一次类推,直到训练完K个LR模型。
对于新来的example,我们将其带入K个训练好的模型中,分别其计算其预测值(前面已经解释过,预测值的大小表示属于某分类的概率),选择预测值最大的那个分类作为其预测分类即可。
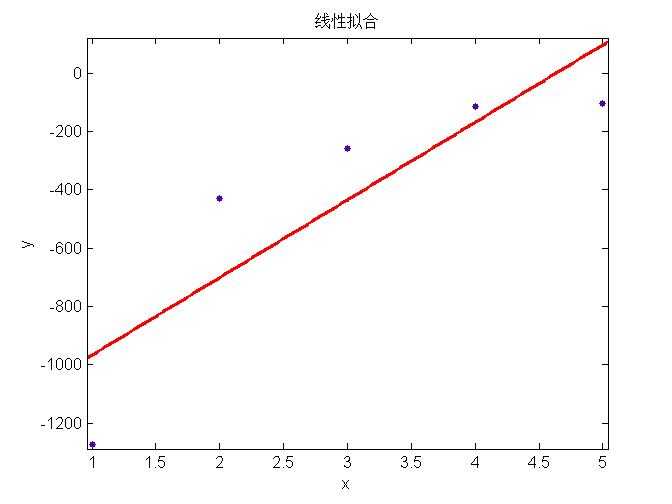
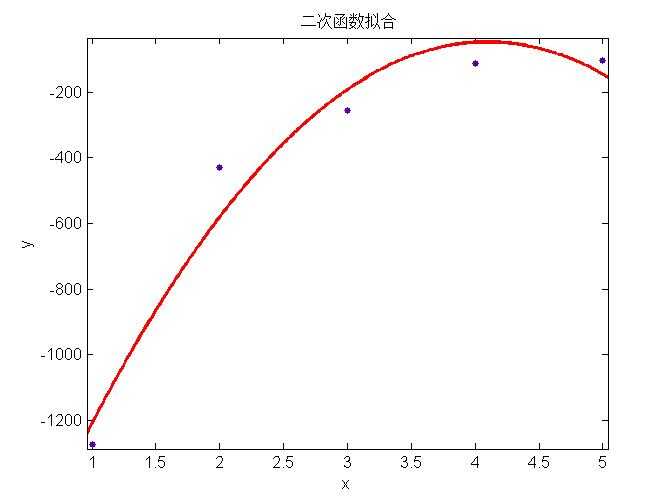
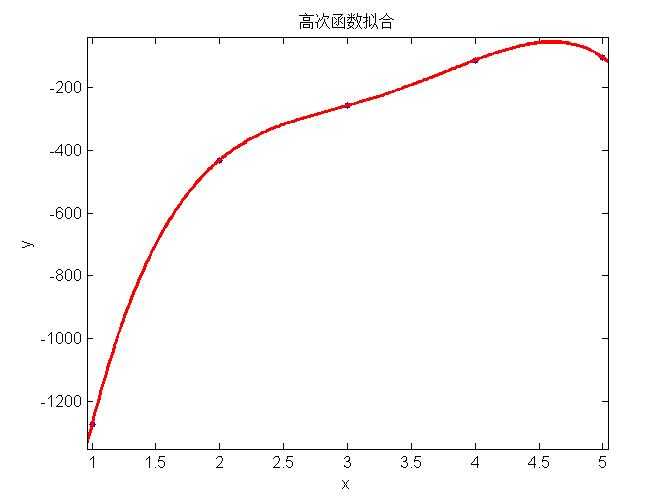
上面三幅图分别表示用简单模型、中等模型和复杂模型对数据进行回归,可以看出左边的模型太简单不能很好的表示数据特征(称为欠拟合, underfitting),中间的模型能够很好的表示模型的特征,右边使用最复杂的模型所有的数据都在回归曲线上,表面上看能够很好的吻合数据,然而当对新的example预测时,并不能很好的表现其趋势,称为过拟合(overfitting)。
Overfitting通常指当模型中特征太多时,模型对训练集数据能够很好的拟合(此时代价函数$J(\theta)$接近于0),然而当模型泛化(generalize)到新的数据时,模型的预测表现很差。
Overfitting的解决方案
在原来的代价函数中加入参数惩罚项如下式所示,注意惩罚项从$j=1$开始,第0个特征是全1向量,不需要惩罚。
代价函数:
$$J(\theta) = \frac{1}{2m}\left[ \sum\limits_{i=1}^{m} (h_\theta(x^{(i)})-y^{(i)})^2 + \lambda \sum\limits_{j=1}^{n}\theta_j^{2}\right]$$
梯度下降参数更新:
$$\theta_0 = \theta_0 - \alpha\frac{1}{m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_0^{(i)}; j = 0$$
$$\theta_j = \theta_j - \alpha \left[ \frac{1}{m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} + \frac{\lambda}{m}\theta_j \right]; j > 1$$
代价函数: $$J(\theta) = -\frac{1}{m} \sum\limits_{i=1}^{m}\left[y^{(i)}\log(h_\theta(x^{(i)})) +(1-y^{(i)})\log(1-h_\theta(x^{(i)}))\right] + \frac{\lambda}{2m}\sum\limits_{j=1}^{n}\theta_j^{2}$$
梯度下降参数更新:
$$\theta_0 = \theta_0 - \alpha\frac{1}{m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_0^{(i)}; j = 0$$
$$\theta_j = \theta_j - \alpha \left[ \frac{1}{m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} + \frac{\lambda}{m}\theta_j \right]; j > 1$$
[1] Andrew Ng Coursera 公开课第二周
[2] Logistic cost function derivative: http://feature-space.com/en/post24.html
标签:
原文地址:http://www.cnblogs.com/python27/p/MachineLearningWeek03.html