标签:
对于一个10x10的网格,从网格的中心出发,向四个方向行进的概率都是1/4,如果行走过程中遇到边界(撞到墙了),那么拒绝这一步行走。那么最终得到的分布是不是均匀分布呢?从结果上来最终得到的是均匀分布。我们可以用Metroplis抽样来解释。首先抽样过程中满足细致平衡,因为我们在撞墙的时候进行了REJECT,算法中隐含的Markov转移矩阵显然也是各态遍历的,所以最终得到均匀分布并不奇怪。
% random_walk bounded 001
% 2 dimensional random walk on a 100x100 lattice
fprintf(‘Random walk on a bounded lattice\n‘);
% lattice size
lsize = 10;
lattice = zeros(lsize);
fprintf(‘Lattice size = %d\n‘, lsize);
% number of random walks
maxn = 1000000;
fprintf(‘Number of random walks = %d\n‘, maxn);
% start from the center
x0 = floor(lsize/2);
y0 = floor(lsize/2);
for i=1:maxn
x1 = x0 + randi(2)*2-3;
y1 = y0 + randi(2)*2-3;
if x1<=0
x1 = 1;
end
if x1>lsize
x1 = lsize;
end
if y1<=0
y1 = 1;
end
if y1>lsize
y1 = lsize;
end
lattice(x1, y1) = lattice(x1,y1) + 1;
x0 = x1;
y0 = y1;
end
mean_value = mean(reshape(lattice, [lsize*lsize,1]));
std_value = std(reshape(lattice, [lsize*lsize,1]));
fprintf(‘Mean = %f std = %g\n‘, mean_value, std_value);
fprintf(‘Std/mean = %f\n‘, std_value/mean_value);
部分输出结果
>> rand_walk_bounded Random walk on a bounded lattice Lattice size = 10 Number of random walks = 1000000 Mean = 10000.000000 std = 117.798 Std/mean = 0.011780
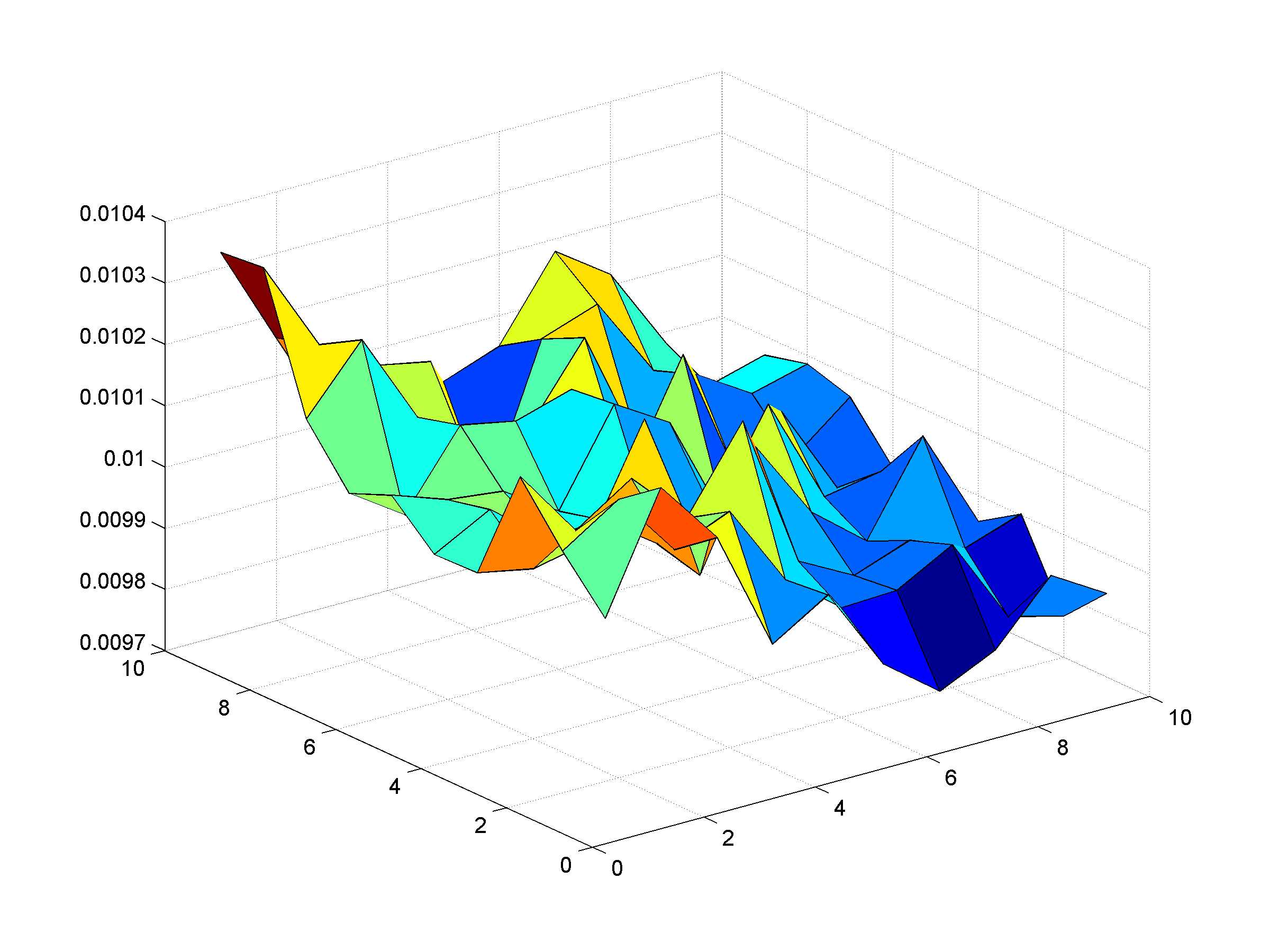
笨手笨脚地画了一个概率分布图(无视花花绿绿的颜色,我不清楚怎么弄下去@_@),注意Z轴的标度。
标签:
原文地址:http://www.cnblogs.com/ch3cooh/p/rand_walk_bounded.html