标签:
Treap,简单的来说就是Tree+Heap,是一颗平衡树,每个节点有两个信息:1.key:当前节点的关键字 ;2.fix:当前节点优先级。key满足二叉排序数的性质,即左儿子都比当前节点小,右儿子都比当前节点大(或相等),fix是一个随机的数,满足小根堆(或大根堆)的性质,fix是为了防止Treap退化成链表的简单优化策略。
如下面的一颗Treap:
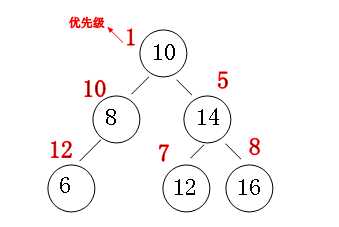
Treap可以进行下面几种操作:插入,查询第k大,旋转,还有其他一些基本操作和一些高级的操作,这里暂不作介绍。
Treap的关联形式是链表,所以要定义一个结构体,其中包含一个指向Treap类型的指针,树的大小,左右儿子的指针。
struct Treap
{
int size,key,fix;
Treap *ch[2];
Treap(int k)//构造函数
{
size=1;
fix=rand();
key=k;
ch[0]=ch[1]=NULL;
}
int compare(int x)const
{
return key==x?-1:x<key?0:1;
}
void Maintain() //计算Treap的大小
{
size=1;
if(ch[0]!=NULL)size+=ch[0]->size;
if(ch[1]!=NULL)size+=ch[1]->size;
}
};
插入的时候,如果当前元素是空的,就用new运算符构造一颗新树(没有儿子节点),如果不是空的,就递归向下直到是 叶子节点。节点之间的联系是以链表的形式建立起来的。
如果新插入的元素的优先级不满足小根堆的性质,则要进行旋转操作,使优先级满足要求。
void insert(Treap *&t,int x)
{
if(t==NULL)t=new Treap(x);
else
{
int d=x < t->key?0:1;
insert(t->ch[d],x);
if(t->fix > t->ch[d]->fix) //破坏了优先级顺序
Rotate(t,d);
}
t->Maintain();
}
当优先级破坏了小根堆的性质的时候,就要进行旋转操作,使重新满足小根堆。
旋转的时候有两种情况
①:左左旋转
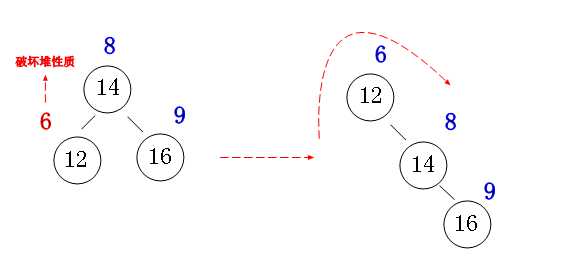
②:右右旋转
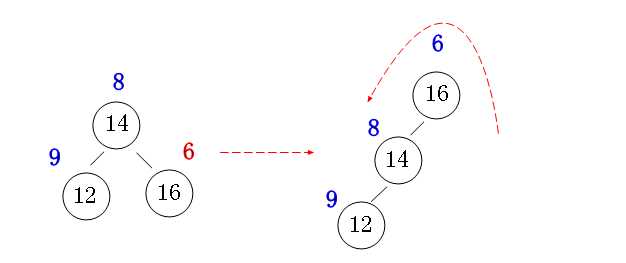
两种情况可以综合到一起,详细见代码。
void Rotate(Treap *&t,int d)
{
Treap *k=t->ch[d]; //临时变量
t->ch[d]=k->ch[d^1]; //用要旋转的节点的“反”儿子替换它的位置
k->ch[d^1]=t; //旋转上去
t->Maintain(); //先计算t的大小,因为现在t是k的子节点。
k->Maintain();
t=k; //根节点上移
}
这里参数的含义是,要处理的根节点是t,ch[d]需要旋转。将参数定义成指针的引用是为了方便修改t的地址。
利用Treap的二叉排序树的性质,左儿子都小于根节点,右儿子大于等于根节点,即可找出第K大元素。
int Kth(Treap*t,int k)
{
if(t==NULL || k<=0 || t->size<k)return -1; //找不到
if(t->ch[0]==NULL && k==1)return t->key; //是当前值
if(t->ch[0]==NULL)return Kth(t->ch[1],k-1); //在右子树找,注意要先出去根节点,所以是k-1
if(t->ch[0]->size >=k )return Kth(t->ch[0],k); //在左子树找,因为左子树上的值都小于当前节点,所以仍然是查找第K大
if(t->ch[0]->size+1==k)return t->key;
return Kth(t->ch[1],k-1-t->ch[0]->size); //注意这里k要减1
}
为了减小空间的占用,在使用完了Treap之后,要及时的把它删掉,因为是链表,所以只能一个一个的删除。
void DeleteTreap(Treap*&t)
{
if(t==NULL)return;
if(t->ch[0]!=NULL)DeleteTreap(t->ch[0]); //删除左子树
if(t->ch[1]!=NULL)DeleteTreap(t->ch[1]); //删除右子树
delete t; //释放内存
t=NULL;
}
题目大意:给n个数,m个查询,每次查询前x个数里面第k大的数,x是升序排列的。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<string>
#define rep(i,n) for(i=1;i<=n;++i)
using namespace std;
const int maxn=1000005;
int n,m,val[maxn];
struct Treap
{
int size,key,fix;
Treap *ch[2];
Treap(int k)
{
size=1;
fix=rand();
key=k;
ch[0]=ch[1]=NULL;
}
int compare(int x)const
{
return key==x?-1:x<key?0:1;
}
void Maintain()
{
size=1;
if(ch[0]!=NULL)size+=ch[0]->size;
if(ch[1]!=NULL)size+=ch[1]->size;
}
};
void Rotate(Treap *&t,int d)
{
Treap *k=t->ch[d];
t->ch[d]=k->ch[d^1];
k->ch[d^1]=t;
t->Maintain();
k->Maintain();
t=k;
}
void insert(Treap *&t,int x)
{
if(t==NULL)t=new Treap(x);
else
{
int d=x < t->key?0:1;
insert(t->ch[d],x);
if(t->fix > t->ch[d]->fix)
Rotate(t,d);
}
t->Maintain();
}
int Kth(Treap*t,int k)
{
if(t==NULL || k<=0 || t->size<k)return -1;
if(t->ch[0]==NULL && k==1)return t->key;
if(t->ch[0]==NULL)return Kth(t->ch[1],k-1);
if(t->ch[0]->size >=k )return Kth(t->ch[0],k);
if(t->ch[0]->size+1==k)return t->key;
return Kth(t->ch[1],k-1-t->ch[0]->size);
}
void DeleteTreap(Treap*&t)
{
if(t==NULL)return;
if(t->ch[0]!=NULL)DeleteTreap(t->ch[0]);
if(t->ch[1]!=NULL)DeleteTreap(t->ch[1]);
delete t;
t=NULL;
}
int main()
{
// freopen("A.in","r",stdin);
// freopen("A.out","w",stdout);
while(scanf("%d%d",&n,&m)!=EOF)
{
int i,index=1,j;
rep(i,n)scanf("%d",&val[i]);
Treap *root=NULL;
rep(i,m)
{
int p;
scanf("%d",&p);
for(j=index;j<=p;j++)
insert(root,val[j]);
index=p+1; //更新index
printf("%d\n",Kth(root,i));
}
DeleteTreap(root); //删除Treap
}
return 0;
}
标签:
原文地址:http://www.cnblogs.com/xionglinlin/p/5079439.html