标签:

class Point { public: double x; double y; public: Point(double =0,double =0); //构造函数,默认值x=y=0 void UpdatePoint(double ,double );//更新Point的坐标值 };

#include "Point.h" Point::Point(double point_x,double point_y) { x=point_x; y=point_y; } void Point::UpdatePoint(double point_x,double point_y) { x=point_x; y=point_y; }

#include<math.h> #include "Point.h" class Frame { public: Point point_Frame; //在某坐标系的坐标 Point point_WorldFrame;//某坐标系的点在世界坐标系中的坐标 Point O_Point; //某坐标系原点相对于世界坐标系的坐标值,默认值为原点 double O_Angle; //某坐标系相对于世界坐标系x轴正方向的转角,默认值为0,单位:弧度;逆时针为+,角度 -pi~pi public: Frame(double =0); //关于原点和转角的构造函数 ,默认值为世界坐标系自身 Frame(Point ,double =0); Point InputPoint_WorldFrame(Point ); // 给定某坐标系中的坐标,返回在世界坐标系的坐标 Point InputPoint_Frame(Point ); // 给定在世界坐标系的坐标,返回某坐标系的坐标 };

#include "Frame.h" Frame::Frame (double InputAngle) { O_Angle=InputAngle*M_PI/180;//转换成弧度制 } Frame::Frame (Point InputOrigin,double InputAngle) { O_Angle=InputAngle*M_PI/180; O_Point=InputOrigin; point_WorldFrame=InputOrigin; //确保在没有调用两个InputPoint函数时,point_WorldFrame仍是在世界坐标系的坐标 } //只不过此时point_Frame是某坐标系的原点 Point Frame::InputPoint_WorldFrame(Point Input_Frame) { point_Frame=Input_Frame; point_WorldFrame.x=O_Point.x+Input_Frame.x*cos(O_Angle)-Input_Frame.y*sin(O_Angle); point_WorldFrame.y=O_Point.y+Input_Frame.x*sin(O_Angle)+Input_Frame.y*cos(O_Angle); return point_WorldFrame; } Point Frame::InputPoint_Frame(Point Input_WorldFrame) { point_WorldFrame=Input_WorldFrame; point_Frame.x=(Input_WorldFrame.x-O_Point.x)*cos(O_Angle)+(Input_WorldFrame.y-O_Point.y)*sin(O_Angle); point_Frame.y=(Input_WorldFrame.y-O_Point.y)*cos(O_Angle)-(Input_WorldFrame.x-O_Point.x)*sin(O_Angle); return point_Frame; }

#include<math.h> #include "Frame.h" class Solver { public: Point Angle[2]; //关节角1,2的角度 Point point_World; // 给定关节角,得到的在世界坐标系中的坐标 int number; //解得关节角的对数,重根视为1 public: Solver(){number=0; } void Pos_calculation(double ,double ,Point );//正运动学为把机器人的关节坐标变换成笛卡尔坐标 void Neg_calculation(double ,double ,Point );// 逆运动学为把机器人的笛卡尔坐标变换成关节坐标 };

#include<math.h> #include"Solver.h" void Solver::Pos_calculation(double length1,double length2,Point Input_Angle) { Angle[0].x=Input_Angle.x*M_PI/180; //给定的两关节角存储在Angle【0】 Angle[0].y=Input_Angle.y*M_PI/180; //得到的世界坐标系的点存储在 point_World point_World.x=length1*cos(Angle[0].x)+length2*cos(Angle[0].y); point_World.y=length1*sin(Angle[0].x)+length2*sin(Angle[0].y); } void Solver::Neg_calculation(double l1,double l2,Point Input_Point) { point_World.x=Input_Point.x; point_World.y=Input_Point.y; double x=point_World.x; double y=point_World.y; double m,delt; double result[2][2]={2*M_PI,2*M_PI,2*M_PI,2*M_PI}; //第一个下标0--关节1,1--关节2 double is_boor[2]={0,0}; double temp[2][4]; //第一个下标0--关节1的临时变量,1--关节2的临时变量 int i,j; m=(x*x+y*y+l2*l2-l1*l1)/(2*l2); delt=pow(y,4)+(x*x-m*m)*y*y; if(delt<0) number=0; else { temp[1][0]=(m*x+sqrt(delt))/(x*x+y*y); // 此时,若number>=0,则关节角1有两种可能,重根视为2个;可能的关节角为 0,1, temp[1][2]=(m*x-sqrt(delt))/(x*x+y*y); // 则temp[0][]依次存储关节1的cos0,sin0,cos1,sin1的计算值,此时可能大于1 if(y==0){ // temp[1][]依次存储关节2的 cos0,sin0,cos1,sin1的计算值, temp[0][0]=(x-l2*temp[1][0])/l1; temp[0][2]=(x-l2*temp[1][2])/l1; if (fabs(temp[1][0])<=1){ result[1][0]=acos(temp[1][0]); result[1][1]=-acos(temp[1][2]); } if (fabs(temp[0][0])<=1){ result[0][0]=-acos(temp[0][0]); result[0][1]=acos(temp[0][2]); } } else{ temp[1][1]=(m-x*temp[1][0])/y; temp[1][3]=(m-x*temp[1][2])/y; for(i=0;i<4;i+=2){ temp[0][i]=(x-l2*temp[1][i])/l1; temp[0][i+1]=(y-l2*temp[1][i+1])/l1; } for(j=0;j<2;j++){ for(i=0;i<4;i+=2){ if(fabs(temp[j][i])<=1) // 对函数取反余弦函数 取值范围 0,π 但关节角的活动范围为 负180-180;因此可以根据sin 值的正负确定关节角的 if(temp[j][i+1]<0) //正负,result 2依次存储关节角2 的两种可能角度 0,1 ,但是也有可能不存在,此时是默认值 2*M_PI result[j][i/2]=-acos(temp[j][i]); //例如 可能角0不存在,则result2【0】= 2*M_PI else result[j][i/2]=acos(temp[j][i]); } } } for(i=0;i<2;i++){ if ((fabs(result[0][i])<=M_PI)&&(fabs(result[1][i])<=M_PI)){ is_boor[i]=1; // 若 (fabs(result[0][i])<=M_PI)&&(fabs(result[1][i])<=M_PI)为真,说明关节角1,2的可能角i--i number++; // 均存在,注:可能会出现一个小于M_PI,一个大于,这样也即是说不能同时存在i-i满足方程 } //这样也相对于方程组无界;is_boor[i]=1表示i--i存在 ,即方程组有解,能找到关节角1,2满足方程组 result[0][i]= result[0][i]*180/M_PI; result[1][i]= result[1][i]*180/M_PI; } if(number==1){ if (is_boor[0]==1){ //若number=1,说明只有一个解,那么 is_boor只有一个为1,将该数据赋值给Angle【0】,Angle【1】为默认值 Angle[0].x=result[0][0]; Angle[0].y=result[1][0]; } else{ Angle[0].x=result[0][1]; Angle[0].y=result[1][1]; } } else if (number==2){ for(i=0;i<2;i++){ Angle[i].x=result[0][i]; //number=2时,两个是解,赋值给Angle【0】【1】 Angle[i].y=result[1][i]; } if((Angle[0].x==Angle[1].x)&&(Angle[0].y==Angle[1].y)) //若两解相同,令number=1; number=1; //最终的效果 无解,Angle【0】【1】为默认值 number=0 } // 只有一解,Angle【0】为解,Angle【1】为默认值 number=1 } // 有两相同解,Angle【0】【1】均为解 number=1 } // 有两不同解,Angle【0】【1】均为解,number=2

#include<math.h> #include "Solver.h" class Robot { public: double L1,L2; Frame JointFrame1,JointFrame2; Point AimPoint_WorldFrame; Solver solver; public: Robot(double =0,double =0); void PTPMove(Frame ,Point );// 给定坐标系和点,求关节角 void PTPMove(Point ); //给定关节角,求关节3的世界坐标系 };

#include "Robot.h" #include<iostream> using namespace std; Robot::Robot(double l1,double l2) { L1=l1; L2=l2; Point O_Joint1,O_Joint2(l1); JointFrame1=Frame(O_Joint1); JointFrame2=Frame(O_Joint2); } void Robot::PTPMove(Frame Input_Frame,Point Input_point) { AimPoint_WorldFrame=Input_Frame.InputPoint_WorldFrame(Input_point); solver.Neg_calculation(L1,L2,AimPoint_WorldFrame); if (solver.number==0) cout<<"该点超出活动范围"<<endl; else if(solver.number==1) cout<<"机械手两关节转角"<<‘(‘<<solver.Angle[0].x<<‘,‘<<solver.Angle[0].y<<‘)‘<<endl; else if(solver.number==2){ cout<<"机械手两关节第一组转角"<<‘(‘<<solver.Angle[0].x<<‘,‘<<solver.Angle[0].y<<‘)‘<<endl; cout<<"机械手两关节第二组转角"<<‘(‘<<solver.Angle[1].x<<‘,‘<<solver.Angle[1].y<<‘)‘<<endl; } solver.number=0; } void Robot::PTPMove(Point Input_Angle) { solver.Pos_calculation(L1,L2,Input_Angle); cout<<"关节3在世界坐标系中的坐标"<<‘(‘<<solver.point_World.x<<‘,‘<<solver.point_World.y<<‘)‘<<endl; }

#include<iostream> #include"Robot.h" using namespace std; int main() { //输入的角度均为XX度,范围-180~180 ,超过自动转换,反解时解得范围-180~180 Point a(5,0),b(15,0),c(25,0); Point P1(0,10),P2(15,20/sqrt(3)),P3(15,0),P4(15,15); Robot myRobot(10,20); Frame WF; Frame TF1(a); Frame TF2(b); Frame TF3(c); cout<<"PTPMove(WF,P1)得到的关节角"<<endl; myRobot.PTPMove(WF,P1); cout<<"PTPMove(TF1,P2)得到的关节角"<<endl; myRobot.PTPMove(TF1,P2); //此点在世界坐标系中的坐标如果为原点,可能会出现错误,例如如果L1=L2,那么关节角1,2分别为Angle,180-Angle,这样存在无数解 cout<<"PTPMove(TF2,P3)得到的关节角"<<endl; myRobot.PTPMove(TF2,P3); cout<<"PTPMove(TF3,P4)得到的关节角"<<endl; myRobot.PTPMove(TF3,P4); return 0; }
程序运行的截图如下:
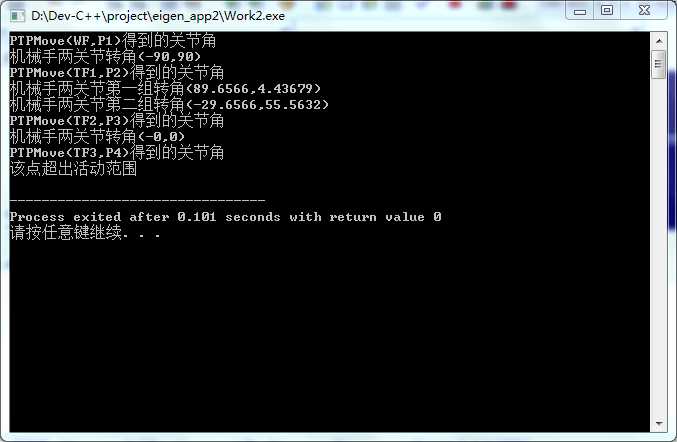
该程序的总结:
1.Slover逆变换时能很好的得出结果,但如果为世界坐标系的原点,有无数解,系统不能解出
2.如果无解,则输出“该点超出活动范围”,且两相同解视为一解
3.此程序可以限定关节角1,2的角度,思路如下,只要能够求出所有解来,只需判断解是否在限定范围内选择性输出,但是程序仍然算出所有解,只不过输出时加以限定即可
4.此程序没有使用到Vector容器
标签:
原文地址:http://www.cnblogs.com/zhibos/p/5080409.html