标签：
1、 比如拿到一个汽车的样本，里面既有以“千米/每小时”度量的最大速度特征，也有“英里/小时”的最大速度特征，显然这两个特征有一个多余。
2、 拿到一个数学系的本科生期末考试成绩单，里面有三列，一列是对数学的兴趣程度，一列是复习时间，还有一列是考试成绩。我们知道要学好数学，需要有浓厚的兴趣，所以第二项与第一项强相关，第三项和第二项也是强相关。那是不是可以合并第一项和第二项呢？
3、 拿到一个样本，特征非常多，而样例特别少，这样用回归去直接拟合非常困难，容易过度拟合。比如北京的房价：假设房子的特征是（大小、位置、朝向、是否学区房、建造年代、是否二手、层数、所在层数），搞了这么多特征，结果只有不到十个房子的样例。要拟合房子特征‐>房价的这么多特征，就会造成过度拟合。
4、 这个与第二个有点类似， 假设在 IR 中我们建立的文档‐词项矩阵中， 有两个词项为 “learn”和“study” ，在传统的向量空间模型中，认为两者独立。然而从语义的角度来讲，两者是相似的，而且两者出现频率也类似，是不是可以合成为一个特征呢？
5、 在信号传输过程中，由于信道不是理想的，信道另一端收到的信号会有噪音扰动，那么怎么滤去这些噪音呢？
将 n维特征映射到 k 维上（k<n） ，这 k 维是全新的正交特征。这 k 维特征称为主元，是重新构造出来的 k 维特征，而不是简单地从 n 维特征中去除其余 n‐k 维特征。
最大方差理论、最小平方误差理论、坐标轴相关度理论
假设我们得到的 2 维数据如下：
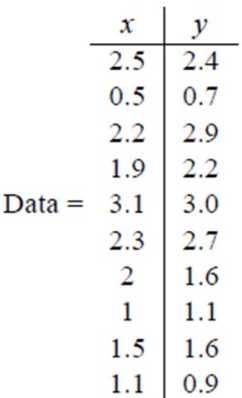
行代表样例，列代表特征，这里有 10 个样例，每个样例两个特征。
第一步，分别求 x 和 y 的平均值，然后对于所有的样例，都减去对应的均值。
这里 x 的均值是 1.81，y 的均值是 1.91，减去后得到
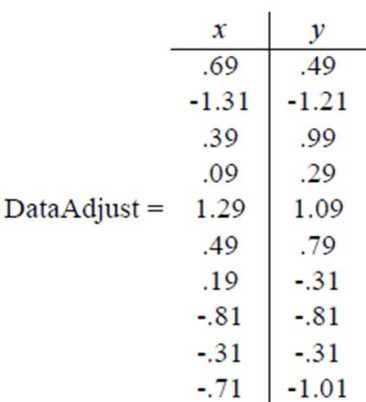
若样本特征之间的方差存在明显差异，需要对特征做方差归一化（可省略）。求每个特征的标准差σ，然后对每个样例在该特征下的数据除以σ。
第二步，求特征协方差矩阵。
如果数据是 3 维，那么协方差矩阵是
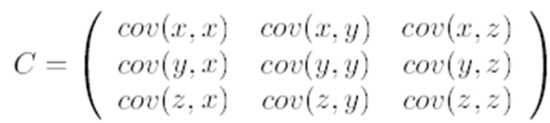
这里只有 x 和 y，求解得
注：对角线上分别是 x 和 y 的方差，非对角线上是协方差。
l 协方差 > 0时，表示 x 和 y 若有一个增，另一个也增；
l 协方差 < 0时，表示一个增，一个减；
l 协方差 = 0 时，两者独立。
l 协方差绝对值越大，两者对彼此的影响越大，反之越小。
求解协方差流程：
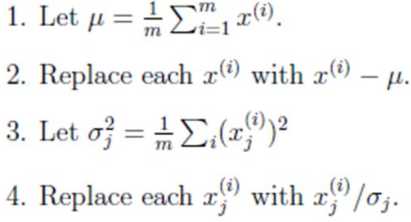
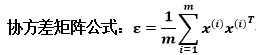
第三步，求协方差的特征值和特征向量，得到
这里的特征向量都归一化为单位向量。
第四步，将特征值按照从大到小的顺序排序，选择其中最大的 k 个，然后将其对应的 k个特征向量分别作为列向量组成特征向量矩阵。
第五步，将样本点投影到选取的特征向量上。
假设样例数为 m，特征数为 n，减去均值后的样本矩阵为 DataAdjust(m*n)，协方差矩阵是 n*n，选取的 k 个特征向量组成的矩阵为EigenVectors(n*k)。
那么投影后的数据为
这样，就将原始样例的 n 维特征变成了 k 维，这 k 维就是原始特征在 k 维上的投影。
本案例令k=1，得到结果：
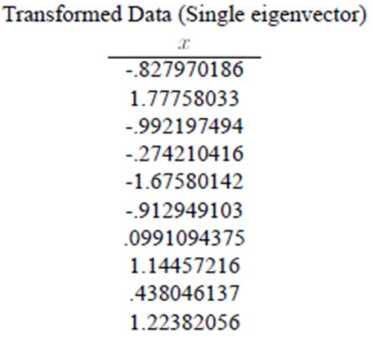
在信号处理中认为信号具有较大的方差， 噪声有较小的方差， 信噪比就是信号与噪声的方差比，越大越好。
如下图所示，样本在横轴上的投影方差较大， 在纵轴上的投影方差较小，那么认为纵轴上的投影是由噪声引起的。因此我们认为，最好的k维特征，是将n维样本点转换为k维后，每一维上的样本方差都很大。
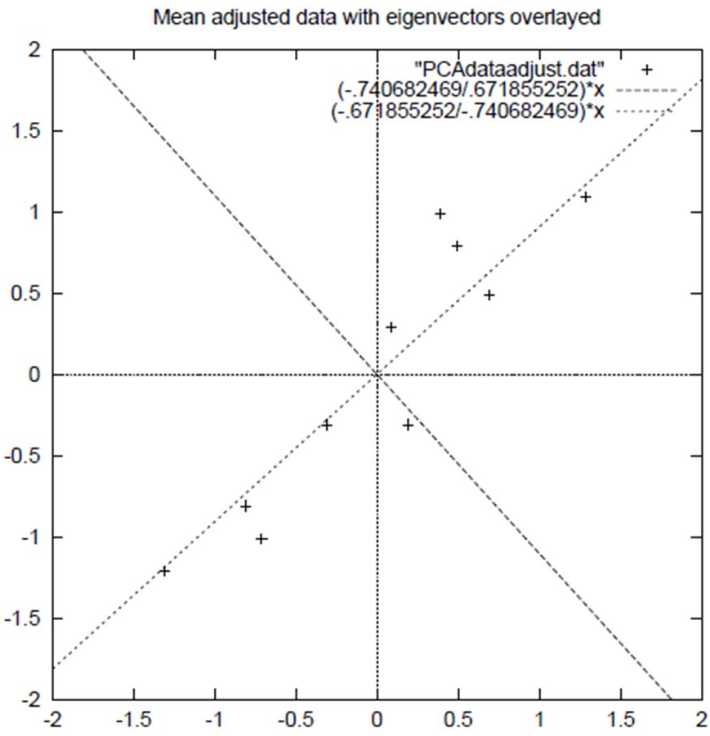
对于下图的5个样本点，假设我们选择两条不同的直线做投影。根据方差最大化理论，左边的好，因为左边投影后的样本点之间的方差最大。
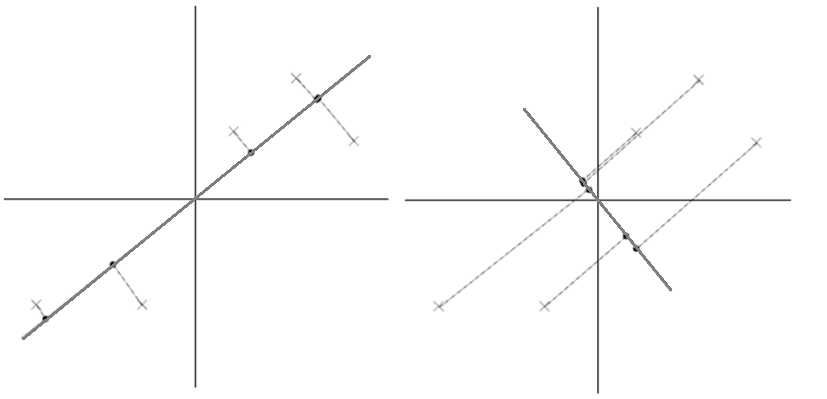
投影
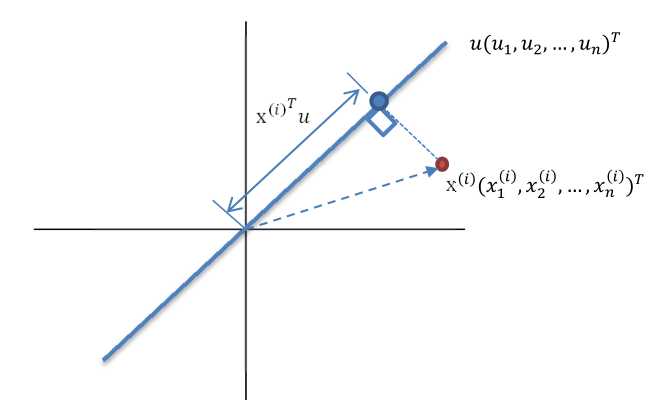
1) 红色点表示样例
2) 蓝色点是在u上的投影点，离原点的距离是<>（即或）
3) u是直线的斜率，也是直线的方向向量，而且是单位向量。
4) 样本点（样例）的每一维特征的均值，和投影到 u上的样本点的均值相等。
最佳的投影向量u，可以使得投影后的样本点方差最大。
在本案例中，已知均值为0，因此方差为
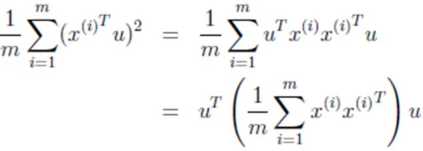
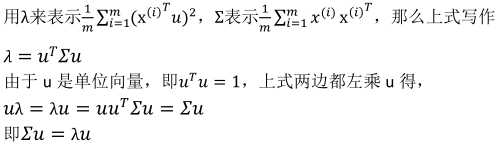
因此，λ就是Σ的特征值，u 是特征向量。最佳的投影直线，是特征值λ最大时对应的特征向量。我们只需要对协方差矩阵进行特征值分解，得到的前 k 大特征值对应的特征向量就是最佳的k维新特征，而且这k维新特征是正交的。
获得的新样本为：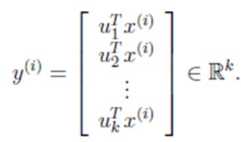
，其中的第 j 维就是在上的投影。
通过选取最大的 k 个 u，使得方差较小的特征（如噪声）被丢弃。
PCA——主成分分析（Principal components analysis ）
标签：
原文地址：http://www.cnblogs.com/sweetyu/p/5085798.html
