electrica writeup

标签：

关于 caesum.com 网上上的题目，分类有Sokoban，Ciphers，Maths，Executables，Programming，Steganography，Misc。题目有点难度，在努力奋战中……

problem 21 Factor
what is the largest prime factor of 806515533049393?
因数分解题，32位int范围在四十亿左右。全球六十多亿人口，很多人还不能上网，而且有局域网的存在，IP本来够用的，因为北美划用了很多，导致了现在的IP不够用，出现了IPv4。64位的int放得下，可以使用int64_t存储，算法嘛，平方筛就可以。
我就不再手写了，直接用linux的命令factor得到答案。
martin@M2037:~$ factor 120
120: 2 3 4 5

problem 4 In days of Olde
提到了Caesar加密，类似汇编的ROL/ROR指令，加密的时候，字符串循环移动。
给了一串字符dvoowlmvgsvdliwblfhvvprhzgyzhs，说用的不是Caesar加密，而是一种更古老的方法。
这难道是要让我翻阅历史，追溯比Caesar加密更古老的加密方法么？
字符少，频率分析不靠谱。大概扫了一眼，看到了oo与vv，应该只是简单的字符替换。
推敲了几分钟，发现用的也是线性变换。只不过从y=a+x变成y=a-x了。

problem 5 Pythagoras
毕达哥拉斯定理在中国称之为勾股定理。这让我想起了《三体》第一部里面把欧姆定律改成电阻定律的场景，说知识是人民智慧的结晶，不应该冠名在一个人头上。不过，话又说回来，勾股定理确实发现得较早些，只是没有传出到国外。
回到正题，像 3,4,5 和 5,12,13 这样的整数勾股数对还有很多，题目要求找出面积为666666的此类三角形。

problem 6 Keyword
简单的EXE加密题，上OllyDbg工具
把exepuzz0.exe 拖到OllyDbg界面里加载。
目前一切正常，还没有反调试的指令。
汇编代码块上鼠标右键，Search for => All referenced strings
Search - Text strings referenced in exepuzz0, item 2
Address = 00401141
Command = PUSH OFFSET 00402010
Comments = ASCII "The solution you need is "

用linux下的命令strings命令输出可打印的字符串，看有什么可疑的。
发现了 cmbipof 和 1‘1B1G1V1g1l1{1
用了标准的显示对话框的函数 MessageBox
martin@M2037:~$ strings exepuzz0.exe
This program must be run under Win32
CODE
`DATA
.idata
.reloc
P.rsrc
fJt(
8hl @
hl @
G@FB;
hl @
h* @
7hl @
hD @
h6 @
hf @
hR @
%X0@
%\0@
%`0@
%d0@
%l0@
cmbipof
The solution you need is
Correct key
Incorrect key
Incorrect key
Blah, see if I care
Blah
USER32.dll
KERNEL32.dll
DialogBoxParamA
EndDialog
MessageBoxA
SendDlgItemMessageA
GetModuleHandleA
1‘1B1G1V1g1l1{1

用了以下几个系统函数
Address Hex dump Command
004011C8 $- FF25 58304000 JMP DWORD PTR DS:[<&USER32.DialogBoxParamA>]
004011CE $- FF25 5C304000 JMP DWORD PTR DS:[<&USER32.EndDialog>]
004011D4 $- FF25 60304000 JMP DWORD PTR DS:[<&USER32.MessageBoxA>]
004011DA $- FF25 64304000 JMP DWORD PTR DS:[<&USER32.SendDlgItemMessageA>]
004011E0 $- FF25 6C304000 JMP DWORD PTR DS:[<&KERNEL32.GetModuleHandleA>]

Address Hex dump Command Comments
004010FF |. A1 0020400 MOV EAX,DWORD PTR DS:[402000] ; ASCII "cmbipof"
00401104 |. 50 PUSH EAX ; /Arg1 => ASCII "cmbipof"
00401105 |. E8 62FFFFF CALL 0040106C ; \exepuzz0.0040106C
0040110A |. 59 POP ECX

这里PUSH字符串指针EAX，通过POP ECX平衡栈。

CPU Disasm
Address Hex dump Command Comments
0040106C /$ 55 PUSH EBP ; exepuzz0.0040106C(guessed Arg1)
0040106D |. 8BEC MOV EBP,ESP
0040106F |. 33D2 XOR EDX,EDX
00401071 |. 8B45 08 MOV EAX,DWORD PTR SS:[ARG.1]
00401074 |. EB 02 JMP SHORT 00401078
00401076 |> 42 /INC EDX
00401077 |. 40 |INC EAX
00401078 |> 8A08 |MOV CL,BYTE PTR DS:[EAX]
0040107A |. 84C9 |TEST CL,CL
0040107C |.^ 75 F8 \JNZ SHORT 00401076
0040107E |. 8BC2 MOV EAX,EDX
00401080 |. 5D POP EBP
00401081 \. C3 RETN

0040106C 这个函数计算字符串的长度，相当于C语言的strlen
第一列是地址，第二列是二进制代码，第三列是反汇编代码，第四列是可添加的注释。
在这一行的最后一列加上注释 strlen(const char*) 方便理解。

我们看到 0040113F |. /75 4C JNE SHORT 0040118D 处的跳转越过了下面这一行。
0040117A |. 68 2A20400 PUSH OFFSET 0040202A ; |Arg3 = ASCII "Correct key"
很显然，我们要阻止这里的跳转发生。
先尝试NOP掉这条指令，让其 fall-through，运行看发生什么。
输入test，显示The solution you need is test

注意到我们的key会通过USER32.MessageBoxA显示出来，其地址为exepuzz0.402094，即数据段的0x00402094处。
Address Hex dump Command Comments
00401178 |. 6A 00 PUSH 0 ; /Arg4 = 0
0040117A |. 68 2A20400 PUSH OFFSET 0040202A ; |Arg3 = ASCII "Correct key"
0040117F |. 68 9420400 PUSH OFFSET 00402094 ; |Arg2 = exepuzz0.402094
00401184 |. 6A 00 PUSH 0 ; |Arg1 = 0
00401186 |. E8 4900000 CALL <JMP.&USER32.MessageBoxA> ; \apphelp.70048650

而输入的字符串存储在数据段的0x0040206C处。
Address Hex dump Command Comments
0040102B |> \68 6C20400 PUSH OFFSET 0040206C ; /lParam = ASCII "test"
00401030 |. 6A 0F PUSH 0F ; |wParam = 15.
00401032 |. 6A 0D PUSH 0D ; |Msg = WM_GETTEXT
00401034 |. 6A 66 PUSH 66 ; |ItemID = 102.
00401036 |. 8B4D 08 MOV ECX,DWORD PTR SS:[ARG.1] ; |
00401039 |. 51 PUSH ECX ; |hDialog => [ARG.1]
0040103A |. E8 9B01000 CALL <JMP.&USER32.SendDlgItemMes ; \USER32.SendDlgItemMessageA

现在，我们要关注 0x0040206C 0x00402094 两个地方进行读写的操作指令。

Address Hex dump Command Comments
00401104 |. 50 PUSH EAX ; /Arg1 => ASCII "cmbipof"
00401105 |. E8 62FFFFF CALL 0040106C ; \exepuzz0.0040106C
0040110A |. 59 POP ECX
0040110B |. 8BD8 MOV EBX,EAX
0040110D |. 68 6C20400 PUSH OFFSET 0040206C ; /Arg1 = ASCII "test"
00401112 |. E8 55FFFFF CALL 0040106C ; \exepuzz0.0040106C
00401117 |. 59 POP ECX
00401118 |. 3BD8 CMP EBX,EAX
0040111A |. 75 21 JNE SHORT 0040113D
这个地方判断输入的key的长度与"cmbipof"这个目前不知道什么鬼的字符串比较长度，不相等就玩完。
那我们就干脆输入cmbipof，运行后说The solution you need is blahone
原来对cmbipof作了rotate操作，即循环减一。

problem 7 Dry Run
第一个编程题，用来练手的。
Given two variables x and y:
set x=0
for y=1 to 100
add y*y+y+1 to x
end for
print x

编程就不用说了，这里可以直接用公式计算的。
1 + 2 + 3 + ... + n = n*(n+1)/2
1² + 2² + 3² + ... + n² = n*(n+1)*(2n+1)/6

结合上面的两个式子在n=100的结果，再加上100。

problem 10 Fibber
斐波拉契数列
题目要求找最小的正整数，满足F[x]=0 mod 2^32
也就是这个斐波拉契数的最低32位数全为0。
我们不需要用int64_t来搜索，直接用int32_t x; 如果发现 x == 0 了，就是解了。

problem 15 Transposition
http://www.caesum.com/game/problems/ciph_2a.php
在计算机没出现之前，大家玩的加密手段主要是替换和移位。
做这道题需要了解一下columnar transposition cipher，去这里https://en.wikipedia.org/wiki/Transposition_cipher
atloflgjnheinisoitlhtnalosnetwatlinlwlrheohawdsestnlkiixeomn

5x12
atloflgjnhei
nisoitlhtnal
osnetwatlinl
wlrheohawdse
stnlkiixeomn

6*10
atloflgjnh
einisoitlh
tnalosnetw
atlinlwlrh
eohawdsest
nlkiixeomn

atlofl
gjnhei
nisoit
lhtnal
osnetw
atlinl
wlrheo
hawdse
stnlki
ixeomn

atlof
lgjnh
einis
oitlh
tnalo
snetw
atlin
lwlrh
eohaw
dsest
nlkii
xeomn

atloflgjnheinisoitlhtnalosnetwatlinlwlrheohawdsestnlkiixeomn
atloflgjnh of all th
einisoitlh
tnalosnetw
atlinlwlrh
eohawdsest
nlkiixeomn

atlofl
gjnhei
nisoit
lhtnal
osnetw
atlinl
wlrheo
hawdse
stnlki
ixeomn

// swap columns
ofallt
hegnij
oinsti
naltlh
etonws
inallt
hewrol
dshwea
lksnit
omienx

ofallthegnijoinstinaltlhetonwsinallthewroldshwealksnitomienx
of all the gni joins tinaltl het onws in all the wrold shw ealks nitomienx
of all the joining he owns in all the world she walks
Of all the gin joints, in all the towns, in all the world, she walks into mine…

gin [d??n]
n.杜松子酒，； 轧棉机； 陷阱
vt.轧棉，用轧棉机去籽； 用陷阱（网）捕捉

Google 了一下这句话，找到电影 Casablanca，中文《北非谍影》，发现电影还挺不错的，于是一边做题一边下载。

problem 13 Imagine

problem 1 Sokoban1
problem 2 Sokoban2
经典的推箱子游戏
题目的编号靠前，现在的浏览器都不怎么支持applet了，不能在浏览器里玩了。
chrome浏览器鼠标右键，inspect element
<applet code="Sok2" width="370" height="320" title="undefined"></applet>
对应链接为 http://www.caesum.com/game/problems/Sok2.class 下载下来

然后编辑一个简单的网页 page.html
martin@M2037:~$ cat page.html
<html>
<head>
<meta http-equiv="Content-Type" content="text/html; charset=utf-8">
<title>html page for appletviewer</title>
</head>
<body class="class">

<applet code="Sok2.class" width="500" height="200"></applet>

</body>
</html>

再使用JDK里面的 appletviewer 打开，JRE是没有这个工具的。
答案肯定需要完成推箱子游戏，但是完成后会显示出答案，还是提交答案到服务器呢？
为了一探究竟，我用 jd-gui 工具反编译了代码。

完成任务后，这边会发送POST请求 ?action=answer&moves=33331113124222... 到服务端。
我就不公开答案了，希望你从做题中找到乐趣。

problem 11 Projectile
过六边形的抛物线。
以地为x轴，垂直向上为y轴，
抛物线过(1/2, sqrt(3)), (1, sqrt(3)/2) 且关于y轴对称，开口朝下
y=-2/sqrt(3) * (x^2 - 7/4);
x=0, 则 y = 7/(2*sqrt(3));
y=0, 则 x = sqrt(7)/2;
y‘ = -4/sqrt(3) * x;
求曲线积分
2*int(sqrt(1+(y‘)^2), 0, sqrt(7)/2)

int(sqrt(1+x^2)) = (asinh(x) + x*sqrt(x^2+1))/2 + C

sqrt(3)/2 * int(sqrt(1+x^2), 0, 2*sqrt(7/3));

; asinh(2)
1.44363547517881034249
; f(x) = x;
"x" is undefined

; a=2*sqrt(7/3)
; asinh(a)/2+a*sqrt(a*a+1)/2-asinh(0)/2
~5.82816295644181367911
; sqrt(3)/2*(asinh(a)/2+a*sqrt(a*a+1)/2-asinh(0)/2)
~5.04733717767402940018
;

; x0 = 0
; x1 = 2+2/sqrt(3)
; x
~3.15470053837925152902
; sqrt(3)/2 * ((asinh(x1) + x1*sqrt(x1^2+1))/2 - (asinh(x0) + x0*sqrt(x0^2+1))/2)

5.047 = 5.828 * sqrt(3)/2 wrong!

信心满满地提交答案，发错是错的。还以为自己的计算哪一步出错了，
The final numerical values, as displayed, were rounded off to three decimal places.
最终数值舍入到小数三位，我没弄错啊，保留三位小数。

problem 22 Coloured Cubes
B 4/6 绿色相对 1/2蓝色相邻
D 1/2/6 红色相邻
四个立方体的颜色布局如下：r/g/b/w分别为红、绿、蓝、白色。

A 2r, 1g, 1b, 2w
B 1r, 2g, 2b, 1w
C 1r, 2g, 1b, 2w
D 3r, 1g, 1b, 1w
================
7r, 6g, 5b, 6w

viewed from front, back, top and bottom, there are always four different colours on display.
假设每个立方体提供一个 R/G/B/W 颜色
那么D的三种红色放置固定了

不想用纸剪，图颜色粘贴成立方体，好在我会简单的Blender建模，决定在Blender展UV得到下面的效果。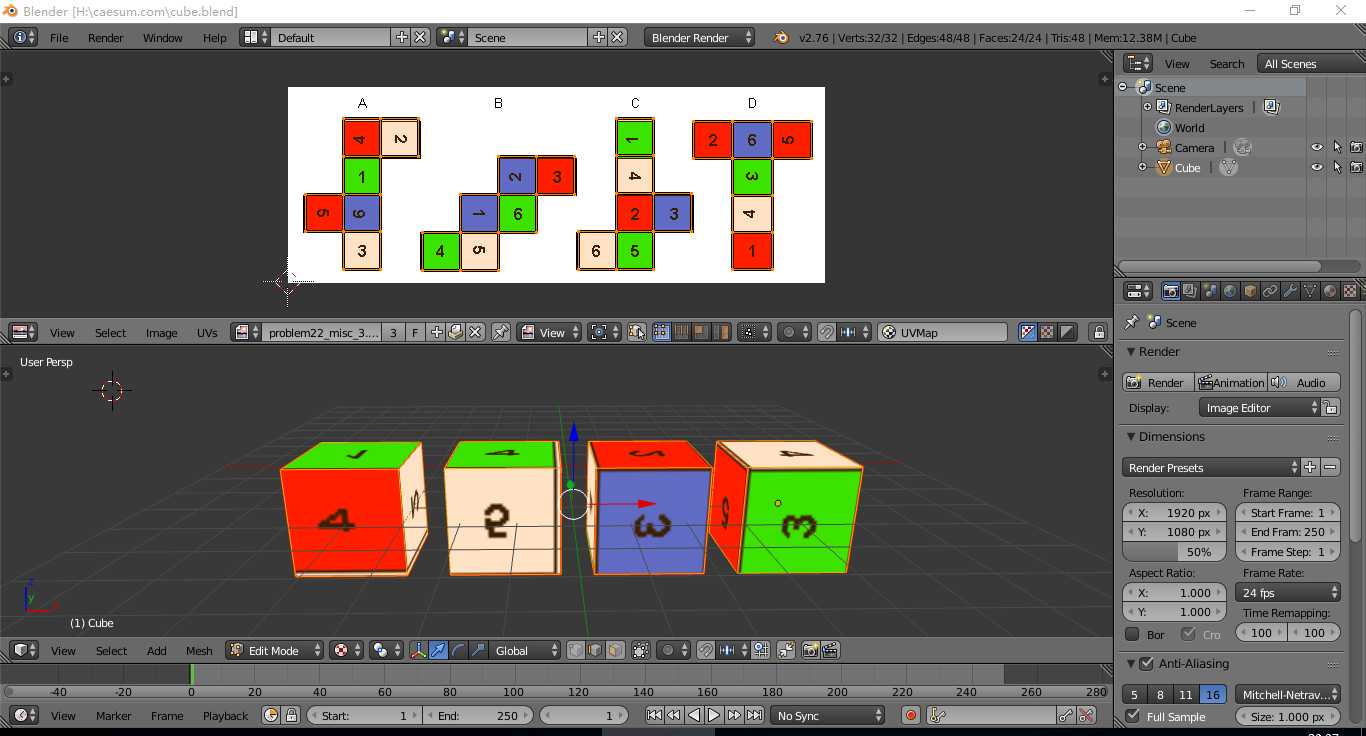

平面图上不好辨认上下左右颜色块，下面立体模型就很容易辨认了。
以为很容易得到答案，在3D世界里对各个方块沿着XYZ轴旋转尝试。
最后还是写了程序，搜索空间不算大，蛮力搜索得到答案。

electrica writeup

标签：

原文地址：http://www.cnblogs.com/Martinium/p/electrica_writeup.html