线性模型（3）——多重线性回归模型

标签：

前面介绍了简单线性回归模型，接下来讲多重线性回归模型。

简单线性回归是针对一个因变量和一个自变量之间的线性回归关系，而多重线性回归是指一个因变量和多个自变量之间的线性回归关系。相对于简单线性回归，多重线性回归更具有实际意义，因为在实际生活中，多因素相互作用非常普遍，同时对因变量造成影响的往往不止一个自变量。

多重线性回归主要解决的问题是
1.估计自变量与因变量之间的线性关系（估计回归方程）
2.确定哪些自变量对因变量有影响（影响因素分析）
3.确定哪个自变量对因变量最影响最大，哪个最小（自变量重要性分析）
4.使用自变量预测因变量，或在控制某些自变量的前提下，进行预测（预测分析）

多重线性回归方程的基本模型为

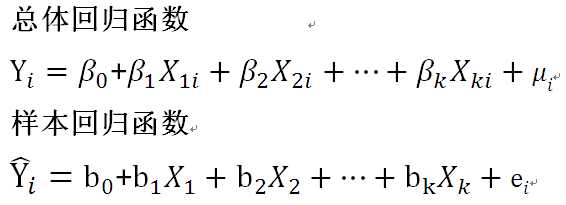
上式中：

β₀和b₀为常数项

β_k和b_k为偏回归系数，表示在其他自变量固定的情况下，某个自变量变化一个单位，相应Y的变换值

μ和e为误差项，即Y变化中不能由现有自变量解释的部分

===============================================

偏回归系数

偏回归系数是多重线性回归和简单线性回归最主要的区别，若要考察一个自变量对因变量的影响，就必须假设其他自变量保持不变。

偏回归系数的标准化：

偏回归系数是有量纲的，由于各自变量的单位量纲不同，导致他们的偏回归系数无法直接比较，如果我们想综合评价各自变量对因变量Y的贡献大小，就需要对偏标准化系数进行标准化，标准化之后的偏回归系数没有单位，系数越大，说明该自变量对Y的影响幅度越大。

偏标准化系数的计算方法为：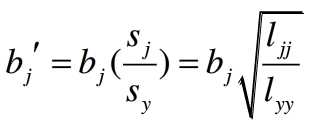

=====================================================

多重线性回归的适用条件

1.线性：因变量与各自变量之间具有线性关系，可通过散点图矩阵来加以判断
2.无自相关性：任意两个xi、xj对应的随机误差μi，μj之间是独立不相关的
3.随机误差服从均值为0，方差为一定值的正态分布
4.在x一定条件下，残差的方差相等(为一常数)，也就是方差齐性

以上四点适用条件和简单线性回归类似，需要通过残差图进行判断，如果不满足，需要作出相应的改变，不满足线性条件需要修改模型或使用曲线拟合，不满足2、3点要进行变量转换，不满足第4点不要采用最小二乘法估计回归参数。

多重线性回归的参数估计方法也使用最小二乘法，但是相比简单线性回归，由于自变量大于1个，计算起来比较繁琐，需要借助计算机，目前主要的统计软件都可以直接给出结果。

===================================================

多重线性回归模型的检验

1.拟合优度检验

多重线性回归拟合优度检验也是通过计算判定系数用来判断，计算原理和方法同简单线性回归一样。这里说一下复相关系数，复相关系数是多重线性回归方程中衡量因变量与所有自变量之间的相关关系的指标，其计算方法也是判定系数的开方，但是复相关系数随着自变量个数的增加而增大，因此使用复相关系数衡量方程的优劣是不妥的，一般采用校正的复相关系数R_ad，计算公式为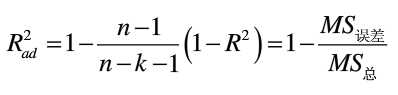


校正的复相关系数当有统计学意义的自变量进入方程时，会增大，当无统计学意义的自变量金融方程时会减小，因此Rad是可以有效的衡量多重线性回归方程的优劣性，也可以作为筛选变量的指标。

还有一个指标是剩余标准差，用来衡量回归方程的精度，剩余标准差小则估计值与观测值接近，反之则相差较大，计算公式为：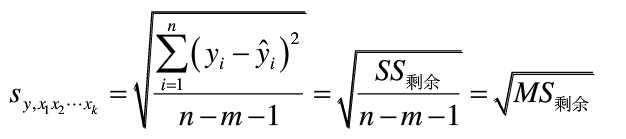

2.回归方程的显著性检验（F检验）

和简单线性回归方程一样，多重线性回归方程的显著性检验也是指对方程中解释变量与被解释变量之间的线性回归关系在总体上是否显著成立做出判断，检验方程中所有被估计的回归系数是否在指定α显著性水平上全部为0，总的来说，若该方程成立，则这些回归系数里面至少有一个不为0，主要有一个不为0，这个方程在形式上就是成立的。检验原理也是根据总差异分解构建F统计量进行检验，统计量的计算公式和简单线性回归一样

对于回归方程Yi=β₀+β₁X₁+β₂x₂+...+β_ix_i+μ_i

提出原假设
H₀:β₁=β₂=β_i=0
H₁:β₁，β₂...β_i不全为0

根据F统计量计算值，并根据显著性水平α查询临界值F_{α (m,n-m-1)}，n为样本量 m为自变量个数

如果F>F_α，则拒绝H0，认为估计出的参数不同时为0，回归方程是显著的
如果F<F_α，则接受H0，认为估计出的参数同时为0，回归模型是不显著的


3.变量的显著性检验（t检验）

在通过回归方程的显著性检验后，我们可以得出至少有一个回归系数不为0的结论，也就是说至少有一个自变量与因变量存在线性关系，这并不意味着每个自变量是这样，在众多的自变量中，到底哪个或那些与因变量存在线性关系呢？这需要对每个回归系数进行分别检验，将没通过检验的自变量从模型中剔除。

检验的方法也是构建t统计量进行t检验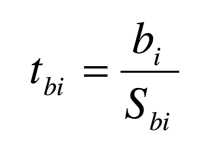

S_bi是第i个偏回归系数的标准误，指的是回归系数的变异程度

对于回归方程Yi=β₀+β₁X₁+β₂x₂+...+β_ix_i+μ_i，以回归系数β₁为例，提出原假设
H₀:β₁等于0
H₁:β₁不等于0
根据显著性水平α查询临界值t_α/2(n-m-1)
如果|t|>t_α/2(n-m-1)，则拒绝H0，认为系数β₁不等于0
如果|t|<t_α/2(n-m-1)，则接受H0，认为系数β₁等于0

====================================================

自变量的筛选

多重线性回归涉及多个自变量，而这些自变量并非全部会对因变量产生影响，因此就涉及自变量的筛选问题，将对因变量产生影响的自变量引入回归模型，其余的剔除掉。将没有通过检验的自变量剔除之后，需要对剩下的数据重建回归方程并重新开始检验，遇到没有通过检验的自变量再删除，再对剩下的数据重建回归方程再重新开始检验，如此反复，直到模型中所有的自变量均通过检验为止，这一过程称为变量筛选，

变量筛选要遵循二个原则：

一、尽可能不漏掉重要的变量。

二、尽可能减少自变量个数，保持模型精简。


目前常用的变量选择的方法有以下几种

1.前向选择法

设定一个进入和剔除标准(P值)，开始回归方程中没有自变量，将k个变量分别与因变量拟合成简单线性回归模型，共有k个，在有统计学意义并且符合进入标准的p个方程中，选择出P值最小或者对因变量贡献最大的那个自变量x_i进入模型，在已经引入x_i的基础上，再分别拟合k-1个自变量的简单线性回归模型，再将其中P值最小或对因变量贡献最大的那个自变量引入模型，如此反复，某变量开始时可能不符合进入标准，但是随着回归方程中进入的变量逐渐增多时，该变量就有可能符合进入标准，这样逐个变量直到不再拟合出具有统计学意义且符合进入标准的简单线性模型为止。

向前选择法的局限：

进入标准选择过小时，可能会导致重要变量无法进入，选择过大时，可能会导致开始进入的变量后期变得无统计学意义而检验不出来。


2.向后选择法

设定一个进入和剔除标准(P值)，将所有自变量与因变量拟合一个回归方程，并进行检验，在对自变量显著性检验中，将无统计学意义并且符合剔除标准的自变量，按照P值最大或对因变量贡献最小原则进行剔除，每剔除一个变量，对回归方程进行重新检验，如此反复，直到回归方程中的自变量全部具有统计学意义并且不符合剔除标准为止。

向后选择法的局限：

剔除标准选择过小时，可能会导致最开始被剔除的变量即使在后期对因变量有较大贡献，也不能被重新引入模型了。剔除标准选择过大时，可能会导致变量不能被有效剔除。

3.逐步回归法

向前发只进不出，向后法只出不进，都有局限，而逐步回归法则是向前和向后的结合，可分为前进逐步回归和后退逐步回归，先以前进逐步回归为例：

设定一个进入和剔除标准(P值)，开始和向前法一样，回归方程中没有自变量，将k个变量分别与因变量拟合成简单线性回归模型，共有k个，在有统计学意义并且符合进入标准的p个方程中，选择出P值最小或者对因变量贡献最大的那个自变量x_i进入模型，在已经引入x_i的基础上，再分别拟合k-1个自变量的简单线性回归模型，再将其中P值最小或对因变量贡献最大的那个自变量x_j引入模型，这时模型中会有两个自变量x_i和x_j，此时按照后退法对这个只有两个自变量的回归模型进行检验，将无统计学意义并且符合剔除标准的自变量，按照P值最大或对因变量贡献最小原则进行剔除，然后再回到变量引入阶段，如此反复，直到没有新的、有统计学意义的自变量可引入模型，且模型中所有变量都具有统计学意义为止。

逐步回归法每引入一个自变量，都对整个模型重新检验，将不符合要求的自变量剔除，这样做到了有进也有出。

逐步回归法的局限是：进入和剔除仅以设定的P值为标准，有时会脱离实际。

4.全面分析法（最优子集法）

顾名思义，就是从所有可能的变量组合中挑出最优者，假设有k个变量，一个变量有两种状态：保留或剔除，那么一共会有2k-1个方程，从中挑出剩余标准差最小的，这种方法最为精确，但是缺点是计算量过大。

5.其他方法

除了上述方法之外，还有最大R2增量法、最小R2增量法、R2选择法、修正R2选择法、Mallow‘s Cp选择法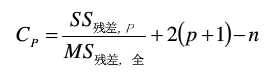

综上所述，自变量的选择有多种方法，但是最终选择的最优回归模型，通常要符合以下几个原则

1.回归模型在整体上有统计学意义
2.回归模型中各参数的估计值的假设检验结果都有统计学意义
3.回归模型中各参数的正负号与其变量在专业上的含义吻合
4.根据回归模型计算出因变量的预测值，在专业上有意义
5.如有多个较好的回归模型，取残差平方和较小且所含变量个数较少者为最佳。

==================================================================

多重共线性问题

多重线性回归会遇到一个问题是多个自变量之间存在相关关系，这种情况会使得回归系数的估计不稳定，预测值的精度降低甚至重要的变量没有引入模型，    

造成多重共线性的原因可能有
1.研究设计不够合理
2.资料收集存在问题
3.自变量间本身就存在相关关系
4.数据中存在异常点
5.样本少而变量多

多重共线性的判断主要有以下几种方式

1.相关系数
两两变量计算相关系数，如果相关系数在0.7以下，一般不会出现太大问题

2.容忍度(tolerance)
值越接近0，共线性越大

3.方差膨胀因子VIF

4.特征根(Eigenvalue)
特征根趋于0，则自变量之间存在共线性

5.条件指数CI(Condition Index)
最大特征根与其余每个特征根比值的平方根，称为条件指数

条件指数在10-30之间，认为是中等程度共线性，若条件指数大于30，则认为是严重的多重共线性。

多重共线性问题的解决

1.变量筛选
通过变量筛选，可以在一定程度上避免共线性的存在

2.使用岭回归或主成分回归分析
有时发现自变量存在多重共线性但是在专业上又不建议剔除的时候，不宜使用最小二乘法估计模型，此时可以使用岭回归或主成分回归分析，这两种估计为有偏估计。

3.增大样本量
通过增大样本量，可以提高估计精度，在一定程度上客服多重共线性

========================================================

多重线性回归的分析步骤

1.考察变量间的相关关系
多重线性回归要满足自变量与因变量呈线性关系，因此第一步就是确定变量间的相关关系是怎样的，可做矩阵散点图进行考察，同时，矩阵散点图还可以发现异常点，异常点对多重线性回归的参数估计影响较大，需要及时发现并做出处理。

2.考察数据分布
考察数据的正态性或方差齐性等问题，如果不符合，需要进行数据变换，数据变换会导致相关关系的改变，需要重新考察相关关系。

3.初步建模
对数据进行初步建模，包括变量筛选等

4.模型诊断，残差分析
建模之后，需要对模型进行各种检验和校正，以保证拟合出的是最佳模型，具体就是显著性检验和残差分析。残差分析主要是检验残差间的线性、独立性、正态性、方差齐性，独立性一般采用Durbin-Watson残差序列相关性检验进行判断，该统计量取值在0-4之间，如果结果在2左右，则可判定残差独立，如果接近0或4，则残差可能存在相关性。正态性可通过直方图进行判断。线性和方差齐性可使用残差图进行判断，残差图是以回归方程的自变量(或因变量的拟合值)为横坐标，以残差为纵坐标，将每一个自变量的残差描在该平面坐标上的散点图，如果残差图均匀分布在以0为中心、与横轴平行的带状区域内，可认为基本满足线性和方差齐性的要求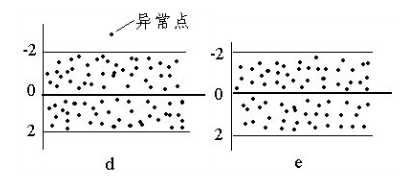

线性模型（3）——多重线性回归模型

标签：

原文地址：http://www.cnblogs.com/xmdata-analysis/p/5093726.html