标签:

"generative algorithm models how the data was generated in order to categorize a signal. It asks the question: based on my generation assumptions, which category is most likely to generate this signal?discriminative algorithm does not care about how the data was generated, it simply categorizes a given signal."
discriminative:
试图找到class之间的差异,进而找到decision boundary,最大可能性地区分数据。他是通过直接学习到$p(y|x)$(例如Logistic regress)或者$X \rightarrow Y\in (0,1,...,k)$(例如perceptron algrithm)
generative:
采取另外一种方式,首先由先验知识prori-knowledge得到 $p(x|y),p(y)$ 然后,通过Bayes rule:$p(y|x) = \frac{p(x|y)p(y)}{p(x)} $来求得$p(y|x)$,其中$p(x)=p(x|y=1)p(y=1)+p(x|y=0)p(y=0)$。这个过程可以看做由先验分布去derive后验分布。当然,在只需要判断出可能性大小的情况下,分母无需考虑,即:$$\arg\max_yp(y|x) = \arg \max_y\frac{p(x|y)p(y)}{p(x)}\\=\arg\max_yp(x|y)p(y)$$
先验知识获取$p(x|y)和p(y)$的方式,是通过现有训练数据样本获得参数的过程。
1. 首先假设一个模型,即样本分布的模型(是伯努利还是高斯分布)
2. 然后通过似然估计likelihood function估计出参数
3. 最后通过贝叶斯公式导出$p(y|x)$
example
数据集:$X=(x_1,x_2)$,$Y\in{0,1}$
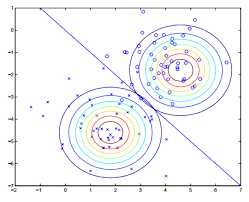
接着通过最大似然估计(max likelihood estimate)估计参数。首先写出log似然函数:$$\ell(\phi,\mu_0,\mu_1,\Sigma) = log\prod_{i=1}^{m}p(x^{(i)},y^{(i)},\mu_0,\mu_1,\Sigma) \\ =log\prod_{i=1}^mp(x^{(i)}|y^{(i)};\mu_0,\mu_1,\Sigma)p(y^{(i)};\phi).$$
然后似然函数$\ell$最大化,即求解似然函数对参数导数为零的点:$$\phi=\frac{1}{m}\sum_{i=1}^{m}1\{y^{(i)}=1\} \\ \mu_0= \frac{\sum_{i=1}^{m}1\{y^{(i)}=0\}x^{(i)}} {\sum_{i=1}^m1\{y^{(i)}=0\}} \\ \mu_1= \frac{\sum_{i=1}^{m}1\{y^{(i)}=1\}x^{(i)}} {\sum_{i=1}^m1\{y^{(i)}=1\}} \\ \Sigma = \frac{1}{m}\sum_{i=1}^m(x^{(i)}-\mu_{y^{(i)}})(x^{(i)}-\mu_{y^{(i)}})^T$$得到参数的估计值$(\phi,\mu_0,\mu_1,\Sigma)$,亦即得到分布函数$p(x|y)$。对照上面的图,$\mu_0,\mu_1$是两个二维向量,在图中的位置是两个正态分布各自的中心点,$\Sigma$则决定者多元正态分布的形状。
![此处输入图片的描述][2]
从这一步可以看出获取参数的方式是“学习”得到的,即从大量样本-先验知识去估计模型,这样想是很自然的逻辑.然而严格的依据却是大数定律law of large numbers (LLN),大数定律的证明很精彩,可自行查找资料。
Generative Learning algorithms
标签:
原文地址:http://www.cnblogs.com/vin-yuan/p/5094960.html