标签:des style blog http color os




// Compute norm of Sobel cv::Sobel(image,sobelX,CV_16S,1,0); cv::Sobel(image,sobelY,CV_16S,0,1); cv::Mat sobel; //compute the L1 norm sobel= abs(sobelX)+abs(sobelY);
The Sobel norm can be conveniently displayed in an image using the optional rescaling parameter of the convertTo method in order to obtain an image in which zero values correspond to white, and higher values are assigned darker gray shades:
// Find Sobel max value double sobmin, sobmax; cv::minMaxLoc(sobel,&sobmin,&sobmax); // Conversion to 8-bit image // sobelImage = -alpha*sobel + 255 cv::Mat sobelImage; sobel.convertTo(sobelImage,CV_8U,-255./sobmax,255);
The result can be seen in the following image:

cv::threshold(sobelImage, sobelThresholded,
threshold, 255, cv::THRESH_BINARY);

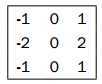
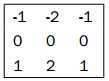
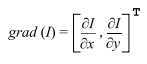
cv::Sobel(image, // input
sobel, // output
image_depth, // image type
xorder,yorder, // kernel specification
kernel_size, // size of the square kernel
alpha, beta); // scale and offset
Since the gradient is a 2D vector, it has a norm and a direction. The norm of the gradient vector tells you what the amplitude of the variation is and it is normally computed as a Euclidean norm (also called L2 norm):
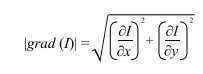
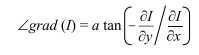
// Sobel must be computed in floating points cv::Sobel(image,sobelX,CV_32F,1,0); cv::Sobel(image,sobelY,CV_32F,0,1); // Compute the L2 norm and direction of the gradient cv::Mat norm, dir; cv::cartToPolar(sobelX,sobelY,norm,dir);

#if ! defined LAPLACIAN
#define LAPLACIAN
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>
class LaplacianZC {
private:
// original image
cv ::Mat img;
// 32-bit float image containing the Laplacian
cv ::Mat laplace;
// Aperture size of the laplacian kernel
int aperture;
public:
LaplacianZC () : aperture(3 ) {}
// Set the aperture size of the kernel
void setAperture( int a) {
aperture = a;
}
// Compute the floating point Laplacian
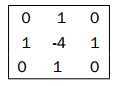
cv ::Mat computeLaplacian( const cv:: Mat &image ) {
// Compute Laplacian
cv ::Laplacian( image, laplace , CV_32F, aperture);
// Keep local copy of the image
// (used for zero-crossing)
img = image. clone();
return laplace;
}
// Get the Laplacian result in 8-bit image
// zero corresponds to gray level 128
// if no scale is provided, then the max value will be
// scaled to intensity 255
// You must call computeLaplacian before calling this
cv ::Mat getLaplacianImage( double scale = -1.0 ) {
if ( scale < 0) {
double lapmin, lapmax;
cv ::minMaxLoc( laplace, &lapmin, &lapmax );
scale = 127 / std ::max(- lapmin, lapmax );
}
cv ::Mat laplaceImage;
laplace .convertTo( laplaceImage, CV_8U , scale, 128);
return laplaceImage;
}
};
#endif
main.cpp:
#include "laplacianZC.h"
int main() {
cv ::Mat image = cv::imread ("../boldt.jpg", 0);
if (! image.data ) {
return 0 ;
}
cv ::namedWindow( "Original Image" );
cv ::imshow( "Original Image" , image);
// Compute Laplacian using LaplacianZC class
LaplacianZC laplacian ;
laplacian .setAperture( 7);
cv ::Mat flap = laplacian.computeLaplacian (image);
cv ::Mat laplace = laplacian.getLaplacianImage ();
cv ::namedWindow( "Laplacian Image" );
cv ::imshow( "Laplacian Image" , laplace);
cv ::waitKey( 0);
return 0 ;
}



// Get a binary image of the zero-crossing
// if the product of the two adjascent pixels is
// less than threshold then this zero-crsooing
// will be ignored
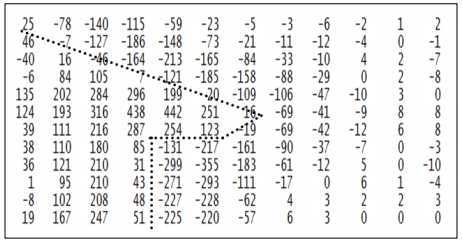
cv ::Mat getZeroCrossing( float threshold = 1.0) {
// Create the iterators
cv ::Mat_< float>::const_iterator it = laplace. begin<float >() + laplace.step1 ();
cv ::Mat_< float>::const_iterator itend = laplace. end<float >();
cv ::Mat_< float>::const_iterator itup = laplace. begin<float >();
// Binary image initialize to white
cv ::Mat binary( laplace.size (), CV_8U, cv::Scalar (255));
cv ::Mat_< uchar>::iterator itout = binary. begin<uchar >() + binary.step1 ();
// negate the input threshold value
threshold *= - 1.0;
for ( ; it != itend; ++it , ++ itup, ++itout) {
// if the product of two adjascent pixel is
// negative the there is a sign change
if (* it * *(it - 1) < threshold ) {
*itout = 0; // horizontal zero-crossing
} else if (*it * *itup < threshold) {
*itout = 0; // vertical zeor-crossing
}
}
return binary;
}
Using the function as follows:
double lapmin, lapmax;
cv ::minMaxLoc( flap,&lapmin ,&lapmax);
// Compute and display the zero-crossing points
cv ::Mat zeros;
zeros = laplacian. getZeroCrossing(lapmax );
cv ::namedWindow( "Zero-crossings" );
cv ::imshow( "Zero-crossings" ,zeros);
Then we get the following result:

Learning OpenCV Lecture 5 (Filtering the Images),布布扣,bubuko.com
Learning OpenCV Lecture 5 (Filtering the Images)
标签:des style blog http color os
原文地址:http://www.cnblogs.com/starlitnext/p/3861440.html