标签:
红黑树是一种自平衡二叉搜索树,每个结点都有一个额外的位(bit),代表了结点的颜色(红色或黑色)。这些代表颜色的位用来确保红黑树在插入和删除时保持基本平衡。
红黑树不保证完全平衡,但是已经足够使得搜索能在O(log n)时间内完成,n为树中元素的个数。插入和删除操作,伴随树结构的重新构造和重新着色,也能在O(log n)时间内完成。
红黑树除了满足二叉搜索树的属性之外,还需要满足以下特性:
1、一个结点要么是红色,要么是黑色
2、根结点是黑色
3、所有的叶子结点不包含数据,也就是指NIL,并且都是黑色
4、如果一个结点是红色的,那么它的子结点都是黑色
5、每一条从给定结点到其后代叶子结点(NIL)的路径都包含相同的黑色结点数量,从根结点到叶子结点(NIL)的黑色结点数量称为黑色树高(black-height)
这些性质强制保证了红黑树的一个特性:从根结点到叶子结点的最长的路径不大于最短路径的两倍。这样可以保证红黑树大体上是平衡的。由于像插入,删除以及搜索在最差情形下运行时间也需要和树的高度成比例,前面的特性在理论上保证了树高的上界,进而使得红黑树在最差情形下也是高效的,而这一点是与一般的二叉搜索树不同的。
这个特性到底是如何确保的呢?是因为前面的第4条和第5条属性共同作用的结果。假设B是满足第5条属性的黑色结点个数,并且是从根结点到叶子结点的最短的路径所包括的结点个数,那么更长的路径只能通过插入红色结点来构造,然而第4条属性不允许插入超过一个连续的红色结点,因为红色结点的子结点必须是黑色结点。因此,如果忽略黑色的NIL叶子结点,则最长的路径由2×B个结点组成,其中红色结点和黑色结点交替出现,如果计算黑色的NIL叶子结点,则最长的路径由2×B-1个结点组成。
与4阶B树(B-tree of order 4)的关系
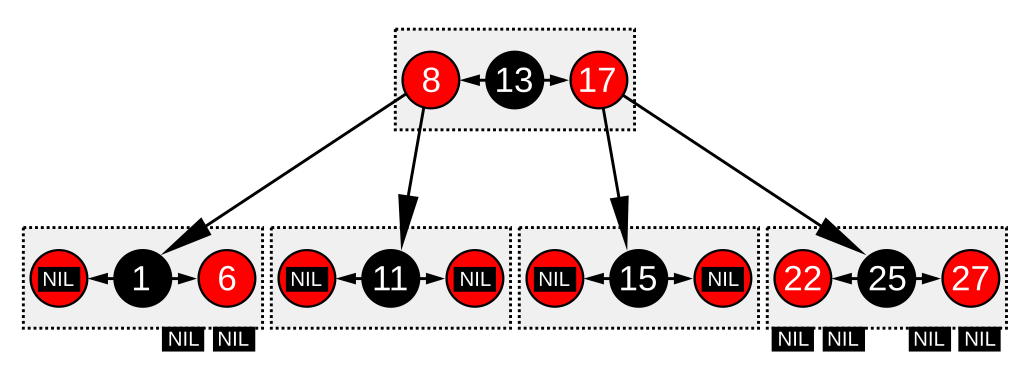
红黑树与一棵4阶B树的结构相似,在4阶B树中,每一个结点可以包含1到3个值,以及2到4个孩子指针。在这样的一棵B树中,每个结点中都包含一个值与红黑树中的黑色结点的值相对应,该值前后的值是可选的(因为总共可以有3个值),共同存在于一个结点当中,前后的值与红黑树中红色结点的值相对应。
了解这种对应关系的一种方法是将红黑树中的红色结点往上移动,这样就和它们的黑色父结点在水平方向上对齐了,同时构造了一个水平方向上的簇(cluster),这样和一棵4阶B树对应起来了。其中每个簇中的最少的填充因子(也就是只有一个值)是最大填充容量(具有三个值)的三分之一。
本文摘自:https://en.wikipedia.org/wiki/Red%E2%80%93black_tree
标签:
原文地址:http://www.cnblogs.com/lengyue365/p/5107646.html