标签：
题意：n个开关m个灯泡，每个开关可以打开多个灯泡（按下其他开关不会导致已经亮的灯泡熄灭），问能否打开所有的灯。
做法：模拟，用tag标记能被打开的灯，遍历一遍所有的灯泡，看是否全部都能被打开。
代码如下：
#include<bits/stdc++.h>
#define rep(i,n) for(i=1;i<=n;i++)
using namespace std;
bool tag[110];
int main()
{
int n,m;
cin>>n>>m;
int i;
rep(i,n)
{
int x,j;
cin>>x;
rep(j,x)
{
int u;
cin>>u;
tag[u]=true;
}
}
rep(i,m)
if(!tag[i])
{
printf("NO");
return 0;
}
printf("YES");
return 0;
}
题意：n个点m条边无自环无重边，找一条下标递增的线段作为尾巴，尾巴末端的点连接的边作为刺，求出尾巴长度*刺的数量的最大值。
思路：如果尾巴确定，那么它的刺的数量也是确定的，只需要用一次dfs找出所有的尾巴，并且在每个节点标记上它作为末端的刺的数量（即连边数）*尾巴长度的值，完成后统计出最大值即可。
做法：从n->1依次枚举每个节点（不能从1->n,从1->n不能把当前节点作为末端)，进行dfs，记录答案。
代码如下：
#include<bits/stdc++.h>
#define rep(i,n) for(i=1;i<=n;i++)
using namespace std;
typedef long long int ll;
const int maxn=100100;
const int maxm=200100;
int fir[maxn],Next[maxm*2],End[maxm*2];
ll vis[maxn],connum[maxn];
int n,m,size;
bool tag[maxn];
void addedge(int x,int y)
{
size++;
Next[size]=fir[x];
fir[x]=size;
End[size]=y;
}
ll dfs(int v)
{
for(int u=fir[v];u;u=Next[u])
{
int ed=End[u];
if(ed<v)
{
if(vis[ed]!=1)vis[v]=max(vis[v],vis[ed]+1);
else vis[v]=max(vis[v],dfs(ed)+1);
}
}
return vis[v];
}
int main()
{
// freopen("B.in","r",stdin);
// freopen("B.out","w",stdout);
scanf("%d%d",&n,&m);
int i;
rep(i,m)
{
int x,y;
scanf("%d%d",&x,&y);
addedge(x,y);
addedge(y,x);
connum[x]++;
connum[y]++;
}
rep(i,n)vis[i]=1;
for(i=n;i>0;i--)
if(vis[i]==1)
vis[i]=dfs(i);
ll ans=0;
//rep(i,n)cout<<vis[i]<<endl;
rep(i,n)
ans=max(ans,vis[i]*connum[i]);
cout<<ans;
}
题意：给多个原始字符串s，可以进行剪切和连接（能够反向），问最少用几个s就可以得到目标字符串t，并输出方案，不能就输出-1.
题意：给出数n的所有质因数，计算出n的所有因子的乘积。
做法：公式，定理太多，直接搬题解
接下来是 d(x)=(a1+1)(a2+1)...(ak+1)的证明。
计算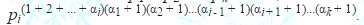
可以用费马小定理：
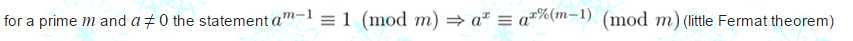
关于快速的计算（a1+1)(a2+1)...(an+1)可以用下面的方法：
这样就可以计算答案了（不用讨论是否是完全平方数的情况），代码如下：
#include<bits/stdc++.h>
#define rep(i,n) for(i=1;i<=n;i++)
using namespace std;
constexpr int maxn=200100;
typedef long long int ll;
map<ll,ll>a;
const ll MOD=1e9+7;
array<ll,maxn>lmul,rmul;
int n;
ll ksm(ll a,ll b,ll c)
{
ll ans=1LL,x=a%c;
while(b)
{
if(b&(1LL))ans=(ans*x)%c;
x=(x*x)%c;
b/=2LL;
}
return ans;
}
int main()
{
freopen("D.in","r",stdin);
freopen("D.out","w",stdout);
ios::sync_with_stdio(false);
int i;
cin>>n;
// bool ok=true;
rep(i,n)
{
ll p;
cin>>p;
a[p]++;
}
ll ans=1LL,tans=1LL;
map<ll,ll>::iterator it;
int num=0;
lmul[0]=rmul[a.size()+1]=1LL;
for(it=a.begin();it!=a.end();++it)
{
++num;
lmul[num]=lmul[num-1]*(it->second+1)%(MOD-1);
}
map<ll,ll>::reverse_iterator rit;
for(rit=a.rbegin();rit!=a.rend();++rit)
{
rmul[num]=rmul[num+1]*(rit->second+1)%(MOD-1);
--num;
}
for(it=a.begin();it!=a.end();++it)
{
++num;
ll u=it->second*(it->second+1LL)/2LL;
ll p=ksm(it->first,u,MOD);
u=lmul[num-1]*rmul[num+1]%(MOD-1);
// cout<<"u="<<u<<endl;
p=ksm(p,u,MOD);
// cout<<"p="<<p<<endl;
ans=ans*p%MOD;
//tans=ksm(it->first,it->second/2LL,MOD);
// if(it->second&1LL)ok=false;
}
//if(ok)ans=ans*tans%MOD;
cout<<ans;
}
*Codeforces Round #338 (Div. 2)
标签：
原文地址：http://www.cnblogs.com/xionglinlin/p/5117160.html
