标签:
参考 《算法设计与分析》 第四章 分治法 Anany Levitin著 翻译版 清华大学出版社
在上一篇文章中,介绍了分治策略的思想,主定理,以及几个用分治策略的经典案例。这一篇文章将继续探讨分治算法的其他应用,包括大整数乘法和Strassen矩阵乘法,最近点对问题和凸包问题这4个算法,一般来说常规的数据结构教程上不包括这些内容。
--------------------------------------------------------------------------------------------------------------------------------------------------
4.5 大整数乘法和Strassen矩阵乘法
两个算法都试图以增加少量的加法为代价,减少乘法运算的次数。
1)大整数乘法
书上讲述的是2个位数都为n位的数相乘,我这里扩展一下,写一个更为一般的方法,任意位数的2个数相乘:
对于任意位数的2个数相乘a * b,写成:
a = a1 * 10^(n1/2) + a0 -----n1为a的位数
b = b1 * 10^(n2/2) + b0 -----n2为b的位数
分治策略就是基于以上变换,将a,b写成前一半数字和后一半数字相加的形式,例如若a = 5423678,那么a1 = 542,a0 = 3678(注意若不是偶数截取较小一半)
这样a和b相乘就可以写为:a * b = { a1 * 10^(n1/2) + a0 } * { b1 * 10^(n2/2) + b0 }
展开后整理得: a * b = a1*b1 * 10^[ (n1+n2)/2 ] + a1*b0 * 10^(n1/2) + a0*b1 * 10^(n2/2) + a0*b0 四项
这样就很容易递归的来求a * b,如果你嫌分解后的数还太大,就可以继续分解。(你可以自己规定在何时结束递归)
实现方法:我们定义一个支持方法Mul(String s1,String s2),用于在结束递归时(在本例中,我定义有一个数是1位时结束递归,直接用普通乘法)计算两个字符串的乘积(为了表示大数,用字符串来接受参数)。有了这个支持方法,分治递归实现两个大数乘法的实现如下:
可以看到如果我们2个字符串都大于1位,那么我们就继续分解a和b。
完整的代码和测试的例子:
BigIntegerMutiply
package Section4;
import java.util.Arrays;
/*第4章 分治法 大整数乘法--计算2个大整数的乘积*/
public class BigIntegerMutiply {
/**
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
long a = 95211154;
long b = 9039;
String s1 = "95211154";
String s2 = "9039";
long suppose = a * b;
long result = Mutiply(s1,s2);
System.out.println(suppose + " " + result);
System.out.println(suppose == result);
}
public static long Mutiply(String a,String b)//用字符串读入2个大整数
{
long result = 0;
if(a.length() == 1 || b.length() == 1) //递归结束的条件
result = Mul(a,b);
else //如果2个字符串的长度都 >= 2
{
String a1 = a.substring(0, a.length() / 2 ); //截取前一半的字符串(较短的一半)
String a0 = a.substring(a1.length(), a.length()); //截取后一半的字符串
//System.out.println(a1);
//System.out.println(a0);
String b1 = b.substring(0, b.length() / 2);
String b0 = b.substring(b1.length(), b.length());
//分治的思想将整数写成这样: a = a1 * 10^(n1/2) + a0, b = b1 * 10^(n2/2),相乘展开得到以下四项
//其中n1,n2为2个整数a,b的位数
result = (long) (Mutiply(a1,b1) * Math.pow(10, a0.length() + b0.length())
+ Mutiply(a1,b0) * Math.pow(10, a0.length()) + Mutiply(a0,b1) * Math.pow(10, b0.length())
+ Mutiply(a0,b0));
}
return result;
}
private static long Mul(String s1,String s2){ //计算2个字符串表示的大整数的乘积
//实际上只有当一个字符串的长度为1时,这个函数才会被调用
int[] a = new int[s1.length()]; //存放大整数s1的各位
int[] b = new int[s2.length()]; //存放大整数s2的各位
for(int i = 0;i < a.length;i++) //将字符‘i‘转化为整数i放入整数数组
a[i] = (int) s1.charAt(i) - 48;
for(int i = 0;i < b.length;i++)
b[i] = (int) s2.charAt(i) - 48;
long num1 = toNum(a);
long num2 = toNum(b);
return num1 * num2;
}
private static long toNum(int[] a){ //将一个整数的位数组转化为它对应的数
long result = 0;
for(int i = 0;i < a.length;i++)
result = result * 10 + a[i];
//System.out.println(result);
return result;
}
}
95211154和903923的乘积:
86063551957142 86063551957142
true
注意,写这个算法仅仅是看看分治是怎样实现的,我的测试用例也算不上是大整数,真正的大整数在普通的计算机上会溢出,计算不出来。一些研究人员的实验显示,在大于600位的整数相乘时,分治策略的性能才超过普通的算法,显然,这么大的数字在常规的计算机上无法运算。
扩展一点,大整数加法怎么做?----------大整数乘法是为了提高效率,减少乘法运算次数而设计的,这里所说的大整数加法不是效率的问题,而是计算机无法表示的问题。例如对于100位甚至1000位的数字,计算机的表示范围显然无法达到,那么应该用数组来存放大整数的每一位,对于进位,直接向前一位加一即可。
2)Strassen矩阵乘法
理论上的分析就不多写了,涉及很多数学上的东西,计算麻烦,直接上书上的图:
分治策略将2个二阶矩阵采用下列方式来计算: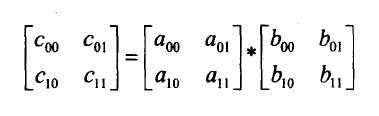
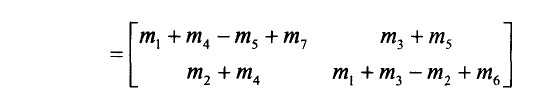
其中: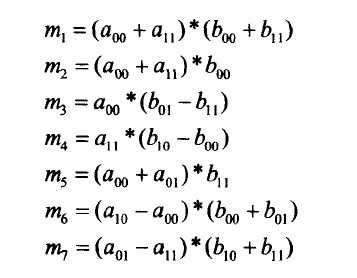
数一下,这样来计算2个二阶矩阵的乘法用了7次乘法,18次加法。而蛮力法用了8次乘法和4次加法。当然,这还不能体现出它的优越性,它的优越性表现在当矩阵的阶趋于无穷大时的渐进效率。
由上面的式子,根据矩阵的相关知识,对于分块矩阵,也可以写成上述形式: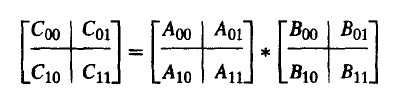
用分治策略来计算矩阵乘法的方法如下:(支持方法较多,详见完整代码)
完整代码:
 Strassen
Strassen
对给出的2个矩阵,乘积输出如下:
输出矩阵:
5 4 7 3
4 5 1 9
8 1 3 7
5 8 7 7
当然,矩阵的阶较大时才能体现出它的优势。
提示:其实二阶的时候结束递归直接蛮力就行了,而且你可以在四阶的时候就结束递归也行,取决于你的实现
--------------------------------------------------------------------------------------------------------------------------------------------------
4.6 用分治法解最近点对问题和凸包问题
问题描述在蛮力法里都介绍过,不再介绍了。
1)最近点对问题
在蛮力法里写了一个2重循环的蛮力算法,时间复杂度是n^2。
a,预排序!
b,在预排序基础上,将点递归的分为左右一半。
实现方式:按照x坐标升序对所求点集进行升序排序。然后递归的将点集分为左右一半,在点集中仅剩2或3个点时用蛮力法结束递归。
注意分治的策略:
划分子问题:每次将问题规模递归的划分为2个一半
合并子问题的解:分别求的2个一半中距离最近的2个点,假设在左一半是点A,点B,右边是点C,点D。再取其距离更小的2个作为暂时的最小值。注意此时AB或CD还不是最终要求的2个点,最小值可能还来自于一个点在左子集中一个点在右子集中。(位于左右子集分割边界上的2个点,一个在左子集中,一个在由子集中)
主方法如下:该方法接受一个点数组,返回其中距离最近的2个点。
注意要得到左右边界的值,然后从左右边界处往两边扩展,看看有没有更小的值。一开始再这个地方犯了错误,见注释。
其他支持方法见完整代码:
 NearestPoint
NearestPoint
输出距离最近的两个点是:
(7,8) (7,9)
这个算法递归的关系式为: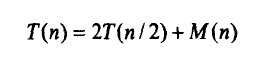
根据主定理,时间复杂度为n * log(n),注意这仅仅是对于划分和合并子问题的解的递推式。还有一个预排序,由于预排序时间复杂也是n * log(n),故它不影响整体的复杂度。
提示:这个例子告诉我们,有时候合并子问题的解并不仅仅是简单的把子问题的解合并起来,它需要一些进一步的处理。最终的解可能并不在子问题的解中,但它来自于对子问题的解进一步的处理结果。
2)凸包问题
描述比较复杂,简单说下,先预排序,预排序后最左和最右的点肯定是凸包中的点。然后可以递归的从内向外扩展凸包,在当前直线的2侧寻找最高点,最高点肯定在凸包中,这里涉及到一些数学知识:
a,首先定义射线p1到p2的左侧:若p1 p2 p构成的顺序是逆时针,称p在射线的左侧
b,三角形p1 p2 p3的面积等于下列行列式的一半: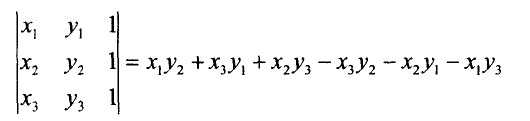
仅当p3在射线p1p2左侧时这个值才为正。
由此我们很容易求p1,p2左侧的最高点(离直线最远的点,这个点即凸包向外扩展得到的新顶点),得到一个最高点后,就得到了2条新边,继续向外扩展,如图: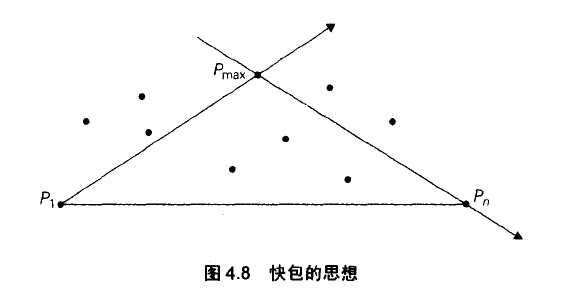
注意我只定义了左侧,其实左右都一样,你把射线方向换一下,处理右侧不就等于处理左侧了吗,免得搞得那么麻烦。详见代码:
以上测试的14个点是精心构造的包含了各种特殊情况的14个点(包括有3点共线,有点的横坐标相等,等等),运行结果如下,有兴趣的可以在坐标系里画一下。
一共有 6 个顶点, 凸包的顶点是:
(-5,7) (6,0) (1,7) (5,4) (-5,-5) (3,-6)
提示:这个代码写的不好,其实每次判断一侧后,就可以将另一侧的点排除掉,这里还没有这样去做。
--------------------------------------------------------------------------------------------------------------------------------------------------
总结:
分治的策略
怎么划分子问题
怎么用递归
规模小的时候结束递归
怎么合并结果
标签:
原文地址:http://www.cnblogs.com/litao0505/p/5123059.html