标签:
混合线性模型也称为多水平线性模型或层次结构线性模型,前面介绍的线性模型,无论是方差分析模型还是线性回归模型,都有三个前提条件:1.正态性、2.独立性、3.方差齐性,但是实际生活中,有时并不能完全满足三个条件,特别是独立性和方差齐性,如果此时仍勉强使用这些一般线性模型,会得出错误结论。
混合线性模型对一般线性模型进行了扩展,除了自变量外。还在模型中加入了一个随机效应变量,使得混合线性模型对内部相关性数据和方差不齐的数据也有很好的效果。
一般线性模型中,假定自变量X是没有随机误差或者随机误差非常小可以忽略不计,这样一来自变量对因变量的作用效应就是固定的,也就是方差、协方差分析模型,具体结构为: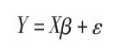
X为自变量矩阵,
β为与X对应的固定效应参数,
ε为残差
Xβ为在X条件下的Y的均值
ε需要满足三个条件:1.均值为0的正态分布、2.独立性、3.方差齐性
通常使用最小二乘法估计β的值
混合线性模型具体结构为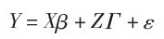
参数含义和传统线性模型一致
只是Z为随机效应变量矩阵,其构造与X相同
Γ为与Z对应的随机效应参数,服从均值为0,方差协方差矩阵为G的正态分布
这里ε只要求满足均值为0的正态分布即可
可以看到,当Z=0时,混合线性模型就成为了一般线性模型和一般线性模型相比,混合线性模型主要是对原随机误差进行了更加精细的分解,从而得到更多的分析信息。
标签:
原文地址:http://www.cnblogs.com/xmdata-analysis/p/5133860.html