标签:
题目
给出两个字符串,找到最长公共子串,并返回其长度。
给出A=“ABCD”,B=“CBCE”,返回 2
子串的字符应该连续的出现在原字符串中,这与子序列有所不同。
解题
注意:
子序列:这个序列不是在原字符串中连续的位置,而是有间隔的,如:ABCDE 和AMBMCMDMEM 最长公共子序列是ADCDE
子串:子串一定在原来字符串中连续存在的。如:ABCDEF 和SSSABCDOOOO最长公共子串是ABCD
参考链接,讲解很详细
根据子串定义,暴力破解

public class Solution { /** * @param A, B: Two string. * @return: the length of the longest common substring. */ public int longestCommonSubstring(String A, String B) { // write your code here if(A == null || B == null ||A.length() ==0 || B.length() ==0) return 0; int lenA = A.length(); int lenB = B.length(); int longest = -1; for(int i=0 ; i <lenA ;i++){ for(int j=0; j <lenB ;j++){ int m = i; int n = j; int sublongest = 0; while(m<lenA && n < lenB){ char ch1 = A.charAt(m); char ch2 = B.charAt(n); if(ch1 == ch2){ m++; n++; sublongest += 1; }else{ break; } } longest = Math.max(longest,sublongest); } } return longest; } }
时间复杂度O(N2M2)
该解法的思路就如前所说,以字符串中的每个字符作为子串的端点,判定以此为开始的子串的相同字符最长能达到的长度。其实从表层上想,这个算法的复杂度应该只有O(n2)因为该算法把每个字符都成对相互比较一遍,但关键问题在于比较两个字符串的效率并非是O(1),这也导致了实际的时间复杂度应该是满足O(n2)和O(n3)。
上面博客中给了第一种动态规划的解法
定义数组C[lenA+1][lenB+1] C[i][j] 表示字符串A 以A[i-1] 结束 B以B[j-1] 最大相同子串的长度
当A[i-1] ==B[j-1] 的时候 C[i][j] = C[i-1][j-1] + 1 理解了子串的定义就很显然的,”连续字符串“
当A[i-1] ==B[j-1] 的时候 C[i][j] = 0
数组中的最大值就是答案了

public class Solution { /** * @param A, B: Two string. * @return: the length of the longest common substring. */ public int longestCommonSubstring(String A, String B) { // write your code here // String A = "cpoe.com code"; // String B = "ccht.com code"; if(A == null || B == null ||A.length() ==0 || B.length() ==0) return 0; int lenA = A.length(); int lenB = B.length(); int [][] C = new int[lenA + 1][lenB + 1]; int longest = -1; for(int i=1;i<= lenA;i++){ for(int j= 1;j<= lenB;j++){ char ch1 = A.charAt(i-1); char ch2 = B.charAt(j-1); if( ch1 == ch2){ C[i][j] = C[i-1][j-1] + 1; }else{ C[i][j] = 0; } longest = Math.max(C[i][j],longest); } } return longest; } }
在求最长公共子序列的题目中我考虑过利用数组进行求解,但是好的解法都没有直接用到我定义的那么简单的数组
对于这个题目,字符串数组表示为:相同字符是 1
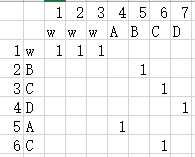
你一定会发现:子串一定在对角线上,连续对角线上1最多的那个就是最长的子串,子串的起始位置就是左上的第一个1,结束位置就是右下的最后一个一,暴力方法就是对每一个点开始的对角线1的个数,最大值就是答案,这个方法其实和上面的暴力方法一个意思的。

public class Solution { /** * @param A, B: Two string. * @return: the length of the longest common substring. */ public int longestCommonSubstring(String A, String B) { // write your code here if(A == null || B == null ||A.length() ==0 || B.length() ==0) return 0; int lenA = A.length(); int lenB = B.length(); int [][] C = new int[lenA ][lenB ]; int longest = -1; for(int i=0;i<lenA;i++){ for(int j= 0;j< lenB;j++){ char ch1 = A.charAt(i); char ch2 = B.charAt(j); if( ch1 == ch2){ C[i][j] = 1; }else{ C[i][j] = 0; } } } for(int i =0;i< lenA;i++){ for(int j=0;j<lenB;j++){ int m = i; int n = j; int sublongest = 0; while(m<lenA && n <lenB){ if(C[m][n] ==1){ sublongest +=1; m++; n++; }else{ break; } } longest = Math.max(longest,sublongest); } } return longest; } }
上面的动态规划解法是在求出数组的同时求对角线上1的个数,上面的分开计算更容易理解,更容易想到动态规划的解法。
上面博客还要其他方法,待更新。。。
lintcode 中等题:longest common substring 最长公共子串
标签:
原文地址:http://www.cnblogs.com/theskulls/p/5134361.html