svm原理解释及推理

    换言之，在进行分类的时候，遇到一个新的数据点x，将x代入f(x) 中，如果f(x)小于0则将x的类别赋为-1，如果f(x)大于0则将x的类别赋为1。

    接下来的问题是，如何确定这个超平面呢？从直观上而言，这个超平面应该是最适合分开两类数据的直线。而判定“最适合”的标准就是这条直线离直线两边的数据的间隔最大。所以，得寻找有着最大间隔的超平面。

    1.2函数间隔与几何间隔

     在超平面w*x+b=0确定的情况下，|w*x+b|能够表示点x到距离超平面的远近，而通过观察w*x+b的符号与类标记y的符号是否一致可判断分类是否正确，所以，可以用(y*(w*x+b))的正负性来判定或表示分类的正确性。于此，我们便引出了函数间隔（functional margin）的概念。 定义函数间隔（用表示）为：

   而超平面(w，b)关于T中所有样本点(xi，yi)的函数间隔最小值（其中，x是特征，y是结果标签，i表示第i个样本），便为超平面(w, b)关于训练数据集T的函数间隔：

                                                                                  = mini  (i=1，...n)

    但这样定义的函数间隔有问题，即如果成比例的改变w和b（如将它们改成2w和2b），则函数间隔的值f(x)却变成了原来的2倍（虽然此时超平面没有改变），所以只有函数间隔还远远不够。

    事实上，我们可以对法向量w加些约束条件，从而引出真正定义点到超平面的距离--几何间隔（geometrical margin）的概念。

    假定对于一个点 x ，令其垂直投影到超平面上的对应点为 x0 ，w 是垂直于超平面的一个向量，为样本x到分类间隔的距离，如下图所示：

有，其中||w||表示的是范数。

  又由于 x0 是超平面上的点，满足 f(x0)=0 ，代入超平面的方程即可算出：

为了得到的绝对值，令乘上对应的类别 y，即可得出几何间隔（用表示）的定义：

1.3最大间隔分类器

 因为现在的目标函数是二次的，约束条件是线性的，所以它是一个凸二次规划问题。这个问题可以用现成的QP (Quadratic Programming) 优化包进行求解。一言以蔽之：在一定的约束条件下，目标最优，损失最小。此外，由于这个问题的特殊结构，还可以通过拉格朗日对偶性（Lagrange Duality）变换到对偶变量 (dual variable) 的优化问题，即通过求解与原问题等价的对偶问题（dual problem）得到原始问题的最优解，这就是线性可分条件下支持向量机的对偶算法，这样做的优点在于：一者对偶问题往往更容易求解；二者可以自然的引入核函数，进而推广到非线性分类问题。那什么是拉格朗日对偶性呢？简单来讲，通过给每一个约束条件加上一个拉格朗日乘子（Lagrange multiplier），定义拉格朗日函数（通过拉格朗日函数将约束条件融合到目标函数里去，从而只用一个函数表达式便能清楚的表达出我们的问题）：

然后令：

 容易验证，当某个约束条件不满足时，例如，那么显然有（只要令即可）。而当所有约束条件都满足时，则最优值为，亦即最初要最小化的量。

 因此，在要求约束条件得到满足的情况下最小化，实际上等价于直接最小化（当然，这里也有约束条件，就是≥0,i=1,…,n）   ，因为如果约束条件没有得到满足，会等于无穷大，自然不会是我们所要求的最小值。具体写出来，目标函数变成了：

这里用表示这个问题的最优值，且和最初的问题是等价的。如果直接求解，那么一上来便得面对w和b两个参数，而又是不等式约束，这个求解过程不好做。不妨把最小和最大的位置交换一下，变成：

交换以后的新问题是原始问题的对偶问题，这个新问题的最优值用来表示。而且有≤，在满足某些条件的情况下，这两者相等，这个时候就可以通过求解对偶问题来间接地求解原始问题。  换言之，之所以从minmax的原始问题，转化为maxmin的对偶问题，一者因为是的近似解，二者，转化为对偶问题后，更容易求解。 下面可以先求L 对w、b的极小，再求L 对的极大。

2.2KTT条件

上文中提到“≤在满足某些条件的情况下，两者等价”，这所谓的“满足某些条件”就是要满足KKT条件。 一般地，一个最优化数学模型能够表示成下列标准形式：

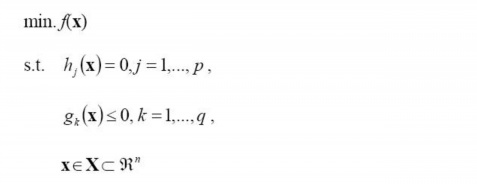
同时，得明白以下两点：

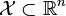• 凸优化的概念： 为一凸集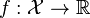，  为一凸函数。凸优化就是要找出一点  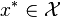，使得每一  满足  。
• KKT条件的意义：它是一个非线性规划（Nonlinear Programming）问题能有最优化解法的必要和充分条件。

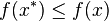    而KKT条件就是指上面最优化数学模型的标准形式中的最小点 x* 必须满足下面的条件：

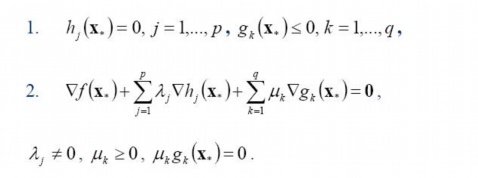
附加：拉格朗日乘子法和KTT条件原理解释：http://www.cnblogs.com/zhangchaoyang/articles/2726873.html

2.3对偶问题的求解方法

（1）、首先固定，要让 L 关于 w 和 b 最小化，我们分别对w，b求偏导数，即令 ∂L/∂w 和 ∂L/∂b 等于零（对w求导结果的解释请看本文评论下第45楼回复）：

将以上结果代入之前的L： 

得到：       

求对的极大，即是关于对偶问题的最优化问题。经过上面第一个步骤的求w和b，得到的拉格朗日函数式子已经没有了变量w，b，只有。从上面的式子得到：

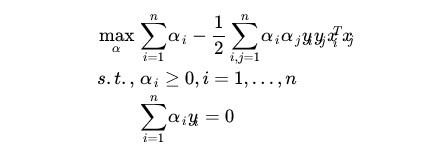
 这样，求出了，根据，即可求出w，然后通过将支持向量带入原方程，即可求出b，最终得出分离超平面和分类决策函数。

2.4线性不可分的情况

 OK，为过渡到下节2.2节所介绍的核函数，让我们再来看看上述推导过程中得到的一些有趣的形式。首先就是关于我们的 hyper plane ，对于一个数据点 x 进行分类，实际上是通过把 x 带入到算出结果然后根据其正负号来进行类别划分的。而前面的推导中我们得到 

因此分类函数为：

 这里的形式的有趣之处在于，对于新点 x的预测，只需要计算它与训练数据点的内积即可（表示向量内积），这一点至关重要，

是之后使用 Kernel 进行非线性推广的基本前提。此外，所谓 Supporting Vector 也在这里显示出来——事实上，所有非Supporting Vector 所对应的系数都是等于零的，

因此对于新点的内积计算实际上只要针对少量的“支持向量”而不是所有的训练数据即可。

为什么非支持向量对应的等于零呢？直观上来理解的话，就是这些“后方”的点——正如我们之前分析过的一样，对超平面是没有影响的，由于分类完全有超平面决定，所以这些无关的点并不会参与分类问题的计算，因而也就不会产生任何影响了。

2.5核函数

特征空间的隐式映射：核函数

 咱们首先给出核函数的来头：在上文中，我们已经了解到了SVM处理线性可分的情况，而对于非线性的情况，SVM 的处理方法是选择一个核函数 κ(⋅,⋅) ，通过将数据映射到高维空间，来解决在原始空间中线性不可分的问题。此外，因为训练样例一般是不会独立出现的，它们总是以成对样例的内积形式出现，而用对偶形式表示学习器的优势在为在该表示中可调参数的个数不依赖输入属性的个数，通过使用恰当的核函数来替代内积，可以隐式得将非线性的训练数据映射到高维空间，而不增加可调参数的个数(当然，前提是核函数能够计算对应着两个输入特征向量的内积)。在线性不可分的情况下，支持向量机首先在低维空间中完成计算，然后通过核函数将输入空间映射到高维特征空间，最终在高维特征空间中构造出最优分离超平面，从而把平面上本身不好分的非线性数据分开。如图7-7所示，一堆数据在二维空间无法划分，从而映射到三维空间里划分：

 而在我们遇到核函数之前，如果用原始的方法，那么在用线性学习器学习一个非线性关系，需要选择一个非线性特征集，并且将数据写成新的表达形式，这等价于应用一个固定的非线性映射，将数据映射到特征空间，在特征空间中使用线性学习器，因此，考虑的假设集是这种类型的函数：

1. 首先使用一个非线性映射将数据变换到一个特征空间F，
2. 然后在特征空间使用线性学习器分类。

    而由于对偶形式就是线性学习器的一个重要性质，这意味着假设可以表达为训练点的线性组合，因此决策规则可以用测试点和训练点的内积来表示：

                                                              

如果有一种方式可以在特征空间中直接计算内积〈φ(x_i · φ(x)〉，就像在原始输入点的函数中一样，就有可能将两个步骤融合到一起建立一个非线性的学习器，这样直接计算法的方法称为核函数方法：

    核是一个函数K，对所有x，z(-X，满足，这里φ是从X到内积特征空间F的映射。

 

2.6核函数如何处理非线性数据

来看个核函数的例子。如下图所示的两类数据，分别分布为两个圆圈的形状，这样的数据本身就是线性不可分的，此时咱们该如何把这两类数据分开呢(下文将会有一个相应的三维空间图)？

                                                                               

  事实上，上图所述的这个数据集，是用两个半径不同的圆圈加上了少量的噪音生成得到的，所以，一个理想的分界应该是一个“圆圈”而不是一条线（超平面）。

如果用 X1 和 X2 来表示这个二维平面的两个坐标的话，我们知道一条二次曲线（圆圈是二次曲线的一种特殊情况）的方程可以写作这样的形式：

                                                                                  

注意上面的形式，如果我们构造另外一个五维的空间，其中五个坐标的值分别为 Z1=X1, Z2=X21, Z3=X2, Z4=X22, Z5=X1X2，那么显然，上面的方程在新的坐标系下可以写作：

 

                                                                                   

关于新的坐标 Z ，这正是一个 hyper plane 的方程！也就是说，如果我们做一个映射 ?:R2→R5 ，将 X 按照上面的规则映射为 Z ，那么在新的空间中原来的数据将变成线性可分的，

从而使用之前我们推导的线性分类算法就可以进行处理了。这正是 Kernel 方法处理非线性问题的基本思想。

 再进一步描述 Kernel 的细节之前，不妨再来看看这个例子映射过后的直观例子。

当然，你我可能无法把 5 维空间画出来，不过由于我这里生成数据的时候就是用了特殊的情形，具体来说，我这里的超平面实际的方程是这个样子（圆心在 X2 轴上的一个正圆）：

                                                                                 

映射之后就可以分了：

                                                          

核函数相当于把原来的分类函数：

映射成：

                          

   而其中的可以通过求解如下 dual 问题而得到的：

                                                                

 

  这样一来问题就解决了吗？似乎是的：拿到非线性数据，就找一个映射  ，然后一股脑把原来的数据映射到新空间中，再做线性 SVM 即可。

不过事实上没有这么简单！其实刚才的方法稍想一下就会发现有问题：在最初的例子里，我们对一个二维空间做映射，选择的新空间是原始空间的所有一阶和二阶的组合，得到了五个维度；

如果原始空间是三维，那么我们会得到 19 维的新空间，这个数目是呈爆炸性增长的，这给  的计算带来了非常大的困难，而且如果遇到无穷维的情况，就根本无从计算了。所以就需要 Kernel 出马了。

  不妨还是从最开始的简单例子出发，设两个向量和，而即是到前面说的五维空间的映射，因此映射过后的内积为：

另外，我们又注意到：

 二者有很多相似的地方，实际上，我们只要把某几个维度线性缩放一下，然后再加上一个常数维度，具体来说，上面这个式子的计算结果实际上和映射

之后的内积的结果是相等的，那么区别在于什么地方呢？

1. 一个是映射到高维空间中，然后再根据内积的公式进行计算；
2. 而另一个则直接在原来的低维空间中进行计算，而不需要显式地写出映射后的结果。

  回忆刚才提到的映射的维度爆炸，在前一种方法已经无法计算的情况下，后一种方法却依旧能从容处理，甚至是无穷维度的情况也没有问题。

    我们把这里的计算两个向量在隐式映射过后的空间中的内积的函数叫做核函数 (Kernel Function) ，例如，在刚才的例子中，我们的核函数为：

为了处理这种情况，SVM 允许数据点在一定程度上偏离一下超平面。例如上图中，黑色实线所对应的距离，就是该 outlier 偏离的距离，如果把它移动回来，就刚好落在原来的超平面上，而不会使得超平面发生变形了。

插播下一位读者@Copper_PKU的理解：“换言之，在有松弛的情况下outline点也属于支持向量SV，同时，对于不同的支持向量，拉格朗日参数的值也不同，如此篇论文《Large Scale Machine Learning》中的下图所示：

  对于远离分类平面的点值为0；对于边缘上的点值在[0, 1/L]之间，其中，L为训练数据集个数，即数据集大小；对于outline数据和内部的数据值为1/L。更多请参看本文文末参考条目第51条。”

  OK，继续回到咱们的问题。我们，原来的约束条件为：

 现在考虑到outlier问题，约束条件变成了：

其中称为松弛变量 (slack variable) ，对应数据点允许偏离的 functional margin 的量。当然，如果我们运行任意大的话，那任意的超平面都是符合条件的了。所以，我们在原来的目标函数后面加上一项，使得这些的总和也要最小：

其中  是一个参数，用于控制目标函数中两项（“寻找 margin 最大的超平面”和“保证数据点偏差量最小”）之间的权重。注意，其中  是需要优化的变量（之一），而  是一个事先确定好的常量。完整地写出来是这个样子：

  用之前的方法将限制或约束条件加入到目标函数中，得到新的拉格朗日函数，如下所示：

 分析方法和前面一样，转换为另一个问题之后，我们先让针对、和最小化：

 将  带回  并化简，得到和原来一样的目标函数：

   不过，由于我们得到而又有（作为 Lagrange multiplier 的条件），因此有，所以整个 dual 问题现在写作：

3   SMO算法

   在上文中，我们提到了求解对偶问题的序列最小最优化SMO算法，但并未提到其具体解法。首先看下最后悬而未决的问题：

等价于求解：

3.1SMO算法的推导

 咱们首先来定义特征到结果的输出函数：

 注：这个u与我们之前定义的实质是一样的。

    接着，重新定义下咱们原始的优化问题，权当重新回顾，如下：

 求导得到：

 代入中，可得

 通过引入拉格朗日乘子转换为对偶问题后，得：

 经过加入松弛变量后，模型修改为：

  从而最终我们的问题变为：

下面要解决的问题是：在上求上述目标函数的最小值。为了求解这些乘子，每次从中任意抽取两个乘子和，然后固定和以外的其它乘子，

使得目标函数只是关于和的函数。这样，不断的从一堆乘子中任意抽取两个求解，不断的迭代求解子问题，最终达到求解原问题的目的。

   而原对偶问题的子问题的目标函数可以表达为：

                                                                其中：

为了解决这个子问题，首要问题便是每次如何选取和。实际上，其中一个乘子是违法KKT条件最严重的，另外一个乘子则由另一个约束条件选取。

 根据KKT条件可以得出目标函数中取值的意义：

这里的还是拉格朗日乘子：

1. 对于第1种情况，表明是正常分类，在边界内部（我们知道正确分类的点）；
2. 对于第2种情况，表明了是支持向量，在边界上；
3. 对于第3种情况，表明了是在两条边界之间；

  而最优解需要满足KKT条件，即上述3个条件都得满足，以下几种情况出现将会出现不满足：

• <=1但是<C则是不满足的，而原本=C
• >=1但是>0则是不满足的，而原本=0
• =1但是=0或者=C则表明不满足的，而原本应该是0<<C

  也就是说，如果存在不满足KKT条件的，那么需要更新这些，这是第一个约束条件。此外，更新的同时还要受到第二个约束条件的限制，

 因此，如果假设选择的两个乘子和，它们在更新之前分别是、，更新之后分别是、，那么更新前后的值需要满足以下等式才能保证和为0的约束：

  其中，是常数。

两个因子不好同时求解，所以可先求第二个乘子的解（），得到的解（）之后，再用的解（）表示的解（）。

 为了求解，得先确定的取值范围。假设它的上下边界分别为H和L，那么有：

 接下来，综合和这两个约束条件，求取的取值范围。

  当y1 != y2时，根据可得，所以有，，如下图所示：

    当y1 = y2时，同样根据可得：，所以有，，如下图所示：

 如此，根据y1和y2异号或同号，可得出的上下界分别为：

 回顾下第二个约束条件，令上式两边乘以y1，可得： 其中，

  因此可以用表示，，从而把子问题的目标函数转换为只含的问题：

 对求导，可得：

化简下： 然后将，，代入上式可得：

 令（表示预测值与真实值之差），，然后上式两边同时除以，得到一个关于单变量的解：

  这个解没有考虑其约束条件，即是未经剪辑时的解。

    然后考虑约束可得到经过剪辑后的的解析解为：

   而b在满足下述条件：

    下更新b：

    最后更新所有，y和b，这样模型就出来了，从而即可求出咱们开头提出的分类函数：