Alice和Bob居住在一个由N座岛屿组成的国家,岛屿被编号为0到N-1。某些岛屿之间有桥相连,桥上的道路是双
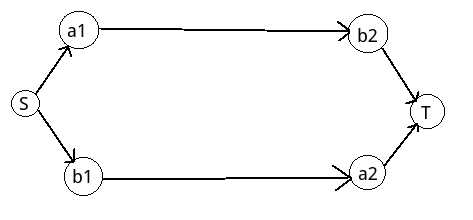
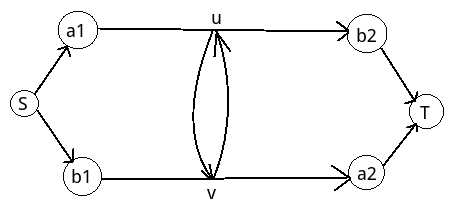
向的,但一次只能供一人通行。其中一些桥由于年久失修成为危桥,最多只能通行两次。Alice希望在岛屿al和a2之间往返an次(从al到a2再从a2到al算一次往返)。同时,Bob希望在岛屿bl和b2之间往返bn次。这个过程中,所有危桥最多通行两次,其余的桥可以无限次通行。请问Alice和Bob能完成他们的愿望吗?
标签:
Alice和Bob居住在一个由N座岛屿组成的国家,岛屿被编号为0到N-1。某些岛屿之间有桥相连,桥上的道路是双
向的,但一次只能供一人通行。其中一些桥由于年久失修成为危桥,最多只能通行两次。Alice希望在岛屿al和a2之间往返an次(从al到a2再从a2到al算一次往返)。同时,Bob希望在岛屿bl和b2之间往返bn次。这个过程中,所有危桥最多通行两次,其余的桥可以无限次通行。请问Alice和Bob能完成他们的愿望吗?
本题有多组测试数据。
每组数据第一行包含7个空格隔开的整数,分别为N、al、a2、an、bl、b2、bn。
接下来是一个N行N列的对称矩阵,由大写字母组成。矩阵的i行j列描述编号i一1和j-l的岛屿间的连接情况,若为“O”则表示有危桥相连:为“N”表示有普通的桥相连:为“X”表示没有桥相连。
|
对于每组测试数据输出一行,如果他们都能完成愿望输出“Yes”,否则输出“No”。
1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 #include<cstring> 5 #include<algorithm> 6 #define maxn 55 7 #define maxm 5050 8 #define inf 1061109567 9 using namespace std; 10 char s[52]; 11 int n,a1,a2,an,b1,b2,bn; 12 struct flow{ 13 int s,t,tot,now[maxn],son[maxm],pre[maxm],val[maxm]; 14 int dis[maxn],head,tail,list[maxn]; 15 bool bo[maxn]; 16 void init(){s=0,t=n+1,tot=1,memset(now,0,sizeof(now));} 17 void put(int a,int b,int c){pre[++tot]=now[a],now[a]=tot,son[tot]=b,val[tot]=c;} 18 void add(int a,int b,int c){put(a,b,c),put(b,a,0);} 19 bool bfs(){ 20 memset(bo,0,sizeof(bo)); 21 head=0,tail=1,list[1]=s,dis[s]=0,bo[s]=1; 22 while (head<tail){ 23 int u=list[++head]; 24 for (int p=now[u],v=son[p];p;p=pre[p],v=son[p]) 25 if (val[p]&&!bo[v]) bo[v]=1,dis[v]=dis[u]+1,list[++tail]=v; 26 } 27 return bo[t]; 28 } 29 int dfs(int u,int rest){ 30 if (u==t) return rest; 31 int ans=0; 32 for (int p=now[u],v=son[p];p&&rest;p=pre[p],v=son[p]) 33 if (val[p]&&dis[v]==dis[u]+1){ 34 int d=dfs(v,min(rest,val[p])); 35 val[p]-=d,val[p^1]+=d,ans+=d,rest-=d; 36 } 37 if (!ans) dis[u]=-1; 38 return ans; 39 } 40 int dinic(){ 41 int ans=0; 42 while (bfs()) ans+=dfs(s,inf); 43 return ans; 44 } 45 }f,g; 46 int main(){ 47 while (~scanf("%d%d%d%d%d%d%d",&n,&a1,&a2,&an,&b1,&b2,&bn)){ 48 a1++,a2++,an<<=1,b1++,b2++,bn<<=1,f.init(); 49 for (int i=1;i<=n;i++){ 50 scanf("%s",s+1); 51 for (int j=1;j<=n;j++) if (s[j]==‘O‘) f.add(i,j,2); else if (s[j]==‘N‘) f.add(i,j,inf); 52 } 53 g=f; 54 f.add(f.s,a1,an),f.add(a2,f.t,an),f.add(f.s,b1,bn),f.add(b2,f.t,bn); 55 g.add(g.s,a1,an),g.add(a2,g.t,an),g.add(g.s,b2,bn),g.add(b1,g.t,bn); 56 if (f.dinic()==an+bn&&g.dinic()==an+bn) puts("Yes"); else puts("No"); 57 } 58 return 0; 59 }
标签:
原文地址:http://www.cnblogs.com/chenyushuo/p/5139556.html