随机森林

标签：

三个臭皮匠顶个诸葛亮
　　　　　　--谁说的，站出来！

1 前言

 　　在科学研究中，有种方法叫做组合，甚是强大，小硕们毕业基本靠它了。将别人的方法一起组合起来然后搞成一个集成的算法，集百家之长，效果一般不会差。其实 也不能怪小硕们，大牛们也有这么做的，只是大牛们做的比较漂亮。

　　在PAC学习框架下（Probably Approximately Correct）, Kearns和Valiant指出，若存在一个多项式级的学习算法来识别一组概念，并且识别正确率很高，那么这组概念是强可学习的；而如果学习算法识别一组概念的正确率仅比随机猜测略好，那么这组概念是弱可学习的。Schapire证明了弱学习算法与强学习算法的等价性问题，这样在学习概念时，只要找到一个比随机猜测略好的弱学习算法，就可以将其提升为强学习算法，而不必直接去找通常情况下很难获得的强学习算法。这为集成学习提供了理论支持。

　　在进一步介绍前，先解释几个常用术语。
　　Bootstraping: 名字来自成语“pull up by your own bootstraps”，意思是依靠你自己的资源，称为自助法，它是一种有放回的抽样方法，它是非参数统计中一种重要的估计统计量方差进而进行区间估计的统计方法。其核心思想和基本步骤如下：
　　（1） 采用重抽样技术从原始样本中抽取一定数量（自己给定）的样本，此过程允许重复抽样。
　　（2） 根据抽出的样本计算给定的统计量T。
　　（3） 重复上述N次（一般大于1000），得到N个统计量T。
　　（4） 计算上述N个统计量T的样本方差，得到统计量的方差。
　　bagging：bootstrap aggregating的缩写。让该学习算法训练多轮，每轮的训练集由从初始的训练集中随机取出的n个训练样本组成，某个初始训练样本在某轮训练集中可以出现多次或根本不出现，训练之后可得到一个预测函数序列h_1，? ?h_n ，最终的预测函数H对分类问题采用投票方式，对回归问题采用简单平均方法对新示例进行判别。

　　boosting: 其中主要的是AdaBoost（Adaptive Boosting）。初始化时对每一个训练例赋相等的权重1／n，然后用该学算法对训练集训练t轮，每次训练后，对训练失败的训练例赋以较大的权重，也就是让学习算法在后续的学习中集中对比较难的训练例进行学习，从而得到一个预测函数序列h_1,?, h_m , 其中h_i也有一定的权重，预测效果好的预测函数权重较大，反之较小。最终的预测函数H对分类问题采用有权重的投票方式，对回归问题采用加权平均的方法对新示例进行判别。

　　Bagging与Boosting的区别：二者的主要区别是取样方式不同。Bagging采用均匀取样，而Boosting根据错误率来取样，因此Boosting的分类精度要优于Bagging。Bagging的训练集的选择是随机的，各轮训练集之间相互独立，而Boostlng的各轮训练集的选择与前面各轮的学习结果有关；Bagging的各个预测函数没有权重，而Boosting是有权重的；Bagging的各个预测函数可以并行生成，而Boosting的各个预测函数只能顺序生成。对于象神经网络这样极为耗时的学习方法。Bagging可通过并行训练节省大量时间开销。

　　在众多单模型中（与集成模型相对应），决策树这种算法有着很多良好的特性，比如说训练时间复杂度较低，预测的过程比较快速，模型容易展示（容易将得到的决策树做成图片展示出来）等。但是同时，单决策树又有一些不好的地方，比如说容易over-fitting，虽然有一些方法，如剪枝可以减少这种情况，但是还是不够的。

　　模型组合（比如说有Boosting，Bagging等）与决策树相关的算法比较多，这些算法最终的结果是生成N(可能会有几百棵以上）棵树，这样可以大大的减少单决策树带来的毛病，有点类似于三个臭皮匠等于一个诸葛亮的做法，虽然这几百棵决策树中的每一棵都很简单（相对于C4.5这种单决策树来说），但是他们组合起来确是很强大。

2 随机森林(Random Forest)

2.1 原理介绍

　　随机森林是一个最近比较火的集成算法，它有很多的优点：

　　(a) 在当前所有算法中，具有极好的准确率/It is unexcelled in accuracy among current algorithms；
　　(b) 能够有效地运行在大数据集上/It runs efficiently on large data bases；
　　(c) 能够处理具有高维特征的输入样本，而且不需要降维/It can handle thousands of input variables without variable deletion；
　　(d) 能够评估各个特征在分类问题上的重要性/It gives estimates of what variables are important in the classification；
　　(e) 在生成过程中，能够获取到内部生成误差的一种无偏估计/It generates an internal unbiased estimate of the generalization error as the forest building progresses；
　　(f) 对于缺省值问题也能够获得很好得结果/It has an effective method for estimating missing data and maintains accuracy when a large proportion of the data are missing

　　随机森林顾名思义，是用随机的方式建立一个森林，森林里面有很多的决策树组成，随机森林的每一棵决策树之间是没有关联的。在得到森林之后，当有一个新的输入样本进入的时候，就让森林中的每一棵决策树分别进行一下判断，看看这个样本应该属于哪一类（对于分类算法），然后看看哪一类被选择最多，就预测这个样本为那一类。

　　打个形象的比喻：森林中召开会议，讨论某个动物到底是老鼠还是松鼠，每棵树都要独立地发表自己对这个问题的看法，也就是每棵树都要投票。该动物到底是老鼠还是松鼠，要依据投票情况来确定，获得票数最多的类别就是森林的分类结果。森林中的每棵树都是独立的，99.9%不相关的树做出的预测结果涵盖所有的情况，这些预测结果将会彼此抵消。少数优秀的树的预测结果将会超脱于芸芸“噪音”，做出一个好的预测。将若干个弱分类器的分类结果进行投票选择，从而组成一个强分类器，这就是随机森林bagging的思想（关于bagging的一个有必要提及的问题：bagging的代价是不用单棵决策树来做预测，具体哪个变量起到重要作用变得未知，所以bagging改进了预测准确率但损失了解释性。）

　　有了树我们就可以分类了，但是森林中的每棵树是怎么生成的呢？
　　每棵树的按照如下规则生成：
　　　　1）如果训练集大小为N，对于每棵树而言，随机且有放回地从训练集中的抽取N个训练样本（这种采样方式称为bootstrap sample方法），作为该树的训练集；
　　 从这里我们可以知道：每棵树的训练集都是不同的，而且里面包含重复的训练样本（理解这点很重要）。这样使得在训练的时候，每一棵树的输入样本都不是全部的样本，使得相对不容易出现over-fitting。
　　　　2）如果每个样本的特征维度为M，在决策树的每个节点需要分裂时，随机从这M个属性中选取出m个属性，满足条件m << M。然后从这m个属性中采用某种策略（比如说信息增益）来选择1个属性作为该节点的分裂属性。

　　　　3）每棵树都尽最大程度的生长，并且没有剪枝过程。由于之前的两个随机采样的过程保证了随机性，所以就算不剪枝，也不会出现over-fitting。

　　一开始我们提到的随机森林中的“随机”就是指的这里的两个随机性。两个随机性的引入对随机森林的分类性能至关重要。由于它们的引入，使得随机森林不容易陷入过拟合，并且具有很好得抗噪能力（比如：对缺省值不敏感）

　　是的，随机森林的基本算法就这么讲完了。是不是觉得很简单？嗯，确实就是这么简单。

2.2 袋外错误率（oob error）　　

　　随机森林有一个重要的优点就是，没有必要对它进行交叉验证或者用一个独立的测试集来获得误差的一个无偏估计。它可以在内部进行评估，也就是说在生成的过程中就可以对误差建立一个无偏估计。
　　我们知道，在构建每棵树时，我们对训练集使用了不同的bootstrap sample（随机且有放回地抽取）。所以对于每棵树而言（假设对于第k棵树），大约有1/3的训练实例没有参与第k棵树的生成，它们称为第k棵树的oob样本。
　　而这样的采样特点就允许我们进行oob估计，它的计算方式如下：（note：以样本为单位）
　　1）对每个样本，计算它作为oob样本的树对它的分类情况（约1/3的树）；
　　2）然后以简单多数投票作为该样本的分类结果；
　　3）最后用误分个数占样本总数的比率作为随机森林的oob误分率

2.3 参数选择

（1） 树的个数

　　较多的子树可以让模型有更好的性能，但同时让你的代码变慢。 你应该选择尽可能高的值，只要你的处理器能够承受的住，因为这使你的预测更好更稳定。

（2） 特征抽样m

　　随机森林分类效果（错误率）与两个因素有关：

　　　　森林中任意两棵树的相关性：相关性越大，错误率越大；
　　　　森林中每棵树的分类能力：每棵树的分类能力越强，整个森林的错误率越低。

　　推荐的做法，对于分类问题，选用sqrt(M)，对于 回归问题，选用M/3 or log2(M).

2.4 特征重要性

　　random forest是个black box，feature importance特性有助于模型的可解释性。简单考虑下，就算在解释性很强的决策树模型中，如果树过于庞大，人类也很难解释它做出的结果。随机森林通常会有上百棵树组成，更加难以解释。好在我们可以找到那些特征是更加重要的，从而辅助我们解释模型。更加重要的是可以剔除一些不重要的特征，降低杂讯。比起pca降维后的结果，更具有人类的可理解性。
　　feature importance有两种常用思路实现。
　　（1） mean decrease in node impurity: feature importance is calculated by looking at the splits of each tree. The importance of the splitting variable is proportional to the improvement to the gini index given by that split and it is accumulated (for each variable) over all the trees in the forest.
　　　　就是计算每棵树的每个划分特征在划分准则（gini或者entropy）上的提升，然后对聚合所有树得到特征权重
　　（2） mean decrease in accuracy: This method, proposed in the original paper, passes the OOB samples down the tree and records prediction accuracy. A variable is then selected and its values in the OOB samples are randomly permuted. OOB samples are passed down the tree and accuracy is computed again. A decrease in accuracy obtained by this permutation is averaged over all trees for each variable and it provides the importance of that variable (the higher the decreas the higher the importance).
　　　　简单来说，如果该特征非常的重要，那么稍微改变一点它的值，就会对模型造成很大的影响。再偷个懒，自己造数据太麻烦，可以直接在OOB数据集对该维度的特征数据进行打乱，重新训练测试，打乱前的准确率减去打乱后的准确率就是该特征的重要度。该方法又叫permute。

　　sklearn中实现的是第一种方法。使用iris数据集我们来看下效果。

　　首先，对于单棵决策树，权重是怎么计算的呢？

iris = load_iris()
X = iris.data
y = iris.target
dt = DecisionTreeClassifier(criterion=‘entropy‘, max_leaf_nodes=3)
dt.fit(X, y)

　　使用Graphviz画出生成的决策树

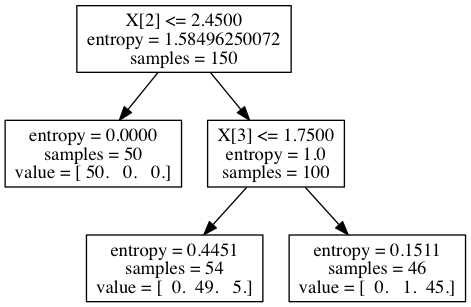
　　sklearn中tree的代码是用Cython编写的，具体这部分的源码在compute_feature_importances方法中

importance_data[node.feature] += (
                        node.weighted_n_node_samples * node.impurity -
                        left.weighted_n_node_samples * left.impurity -
                        right.weighted_n_node_samples * right.impurity)

　　根据上面生成的树，我们计算特征2和特征3的权重

　　　　特征2： 1.585*150 - 0*50 - 1.0*100 = 137.35

　　　　特征3： 1.0*100 - 0.445*54 - 0.151*46 = 69.024

　　归一化之后得到[0, 0, 0.665, 0.335] 我们算的结果和sklearn输出的结果相同。

　　得到每课树的权重之后，sklearn聚合得到结果，具体代码如下：

def feature_importances_(self):
        """Return the feature importances (the higher, the more important the
           feature).

        Returns
        -------
        feature_importances_ : array, shape = [n_features]
        """
        check_is_fitted(self, ‘n_outputs_‘)

        if self.estimators_ is None or len(self.estimators_) == 0:
            raise ValueError("Estimator not fitted, "
                             "call `fit` before `feature_importances_`.")

        all_importances = Parallel(n_jobs=self.n_jobs, backend="threading")(
            delayed(getattr)(tree, ‘feature_importances_‘)
            for tree in self.estimators_)

        return sum(all_importances) / len(self.estimators_)

参考文章

(1) http://www.cnblogs.com/maybe2030/p/4585705.html#_label5
(2) http://blog.datadive.net/interpreting-random-forests/
(3) http://www.csdn.net/article/2015-10-08/2825851
(4) http://blog.datadive.net/random-forest-interpretation-with-scikit-learn/
(5) http://jasonding1354.github.io/2015/07/23/Machine%20Learning/%E3%80%90%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0%E5%9F%BA%E7%A1%80%E3%80%91%E9%9A%8F%E6%9C%BA%E6%A3%AE%E6%9E%97%E7%AE%97%E6%B3%95/
(6) http://www.add-for.com/blog/2015/10/10/ensemble-methods-randomforests/

随机森林

标签：

原文地址：http://www.cnblogs.com/yxzfscg/p/5142620.html