标签:
题目链接:http://www.lydsy.com/JudgeOnline/problem.php?id=2705
令
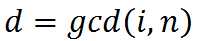
则
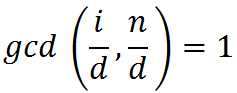
满足上式的 i 的数量就是
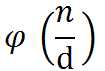
每个 d 对答案的贡献是
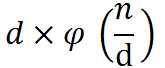
所以 O ( sqrt ( n ) ) 枚举 d,将对答案的贡献值累加起来,答案就是
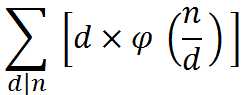
欧拉函数根据定义暴力计算就行了


1 #include <cstdio> 2 #include <cmath> 3 #define rep(i,l,r) for(int i=l; i<=r; i++) 4 using namespace std; 5 typedef long long ll; 6 ll n,m,ans=0; 7 ll phi(ll x){ 8 int ret = x; 9 for(int i = 2; i * i <= x; i++){ 10 if (!(x % i)){ 11 ret = ret / i * (i - 1); 12 while (!(x % i)) x /= i; 13 } 14 } 15 if (x > 1) ret = ret / x * (x - 1); 16 return ret; 17 } 18 int main(){ 19 scanf("%lld",&n); m = floor(sqrt(n)); 20 rep(i,1,m){ 21 if (!(n % i)){ 22 ans += i * phi(n / i); 23 if (i * i != n) ans += (n / i) * phi(i); 24 } 25 } 26 printf("%lld\n",ans); 27 return 0; 28 }
标签:
原文地址:http://www.cnblogs.com/jimzeng/p/bzoj2705.html