3.2 一般的哈尔空间Vj

标签：

例3.2给予我们继续往下面做的动力。很明显的我们对于g（t）的逼近还是太粗糙了.很自然的，我们会想到，如果继续细分我们的短点，比如每1/2取一个值，甚至每1/4取一个值，那么就会有更好的逼近效果。

• 不同分辨率的分段常函数

有没有一种能在“半整数”点和整数点间断的常整数分段函数？我们可以采用与这个类似的处于V₀空间里的函数进行描述。对从门函数引出的Φ（t）进行缩放便可以达到我们的目的

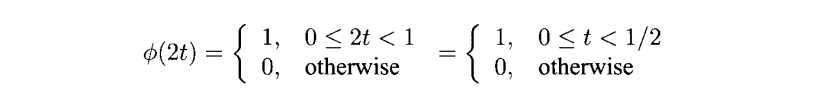
可以看出，这个函数的支撑集是[0,1/2)，那么对它进行尺度变换之后的函数是什么样子呢？由于。从高中的平移知识不难看出这个东西其实就是向右平移了1/2个单位（注意不是一个单位）。那么更一般的来说，也就是平移了k/2个单位。

按照上面的规律，不难得出分段在能被1/4整除的点的常整数分段函数的表达式Φ（4t），又或者分段在偶数点的常整数分段函数Φ（(1/2)t）。这些函数我们在图3.6画出

（译者注：本段对于原文有所删减）

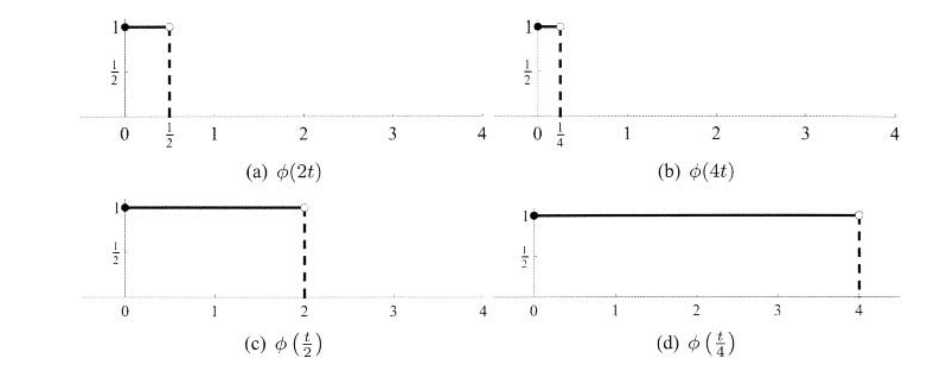
图3.6 函数

• V_j空间的定义

 定义3.2（v_j空间）V_j空间的定义如下所示

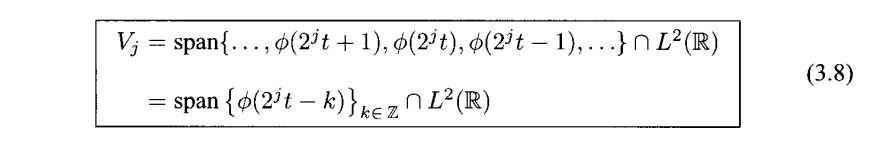
 为了描述v_j ，j∈Z，我们给出一些新的概念，它们如下

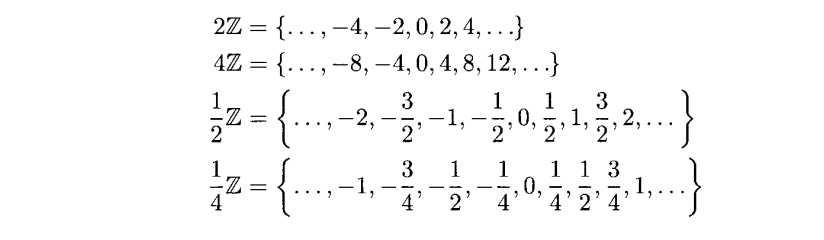
 并且对于j∈Z

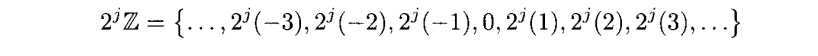
以后，我们的2Z就代表偶整数，1/2 Z就代表“半整数”，1/4就代表“四分之一整数“。我们不难发现V_j 是包含在2^-j处有断点的常分段函数。

我们下面来看一些例子

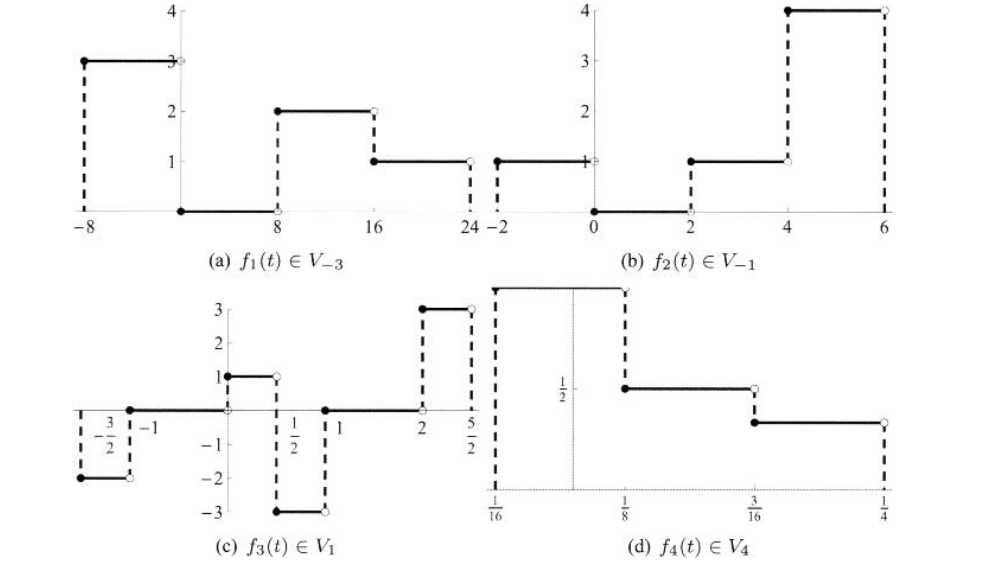
例3.3 （V_j里面的函数）画出以下函数

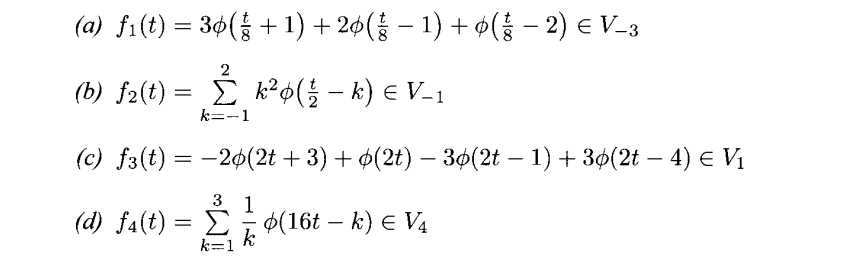
解：

 （译者注：我真的懒了-  -，这些相信读者不会陌生，看小波的人起码初中的函数变换是会的吧，不多叙述了）

•  函数Φ_j,k（k）的定义

 在练习3.7你会知道对于j∈Z来说，{Φ（2^jt-k）}_k∈z是线性无关的，同时，在练习3.8你会知道V_j是L²（R）的子空间。同时，在Vj空间的函数都能通过{Φ（2^jt-k）}_k∈z线性变换而得。所以{Φ（2^jt-k）}_k∈z是这个空间的一组基。在练习3.9你会知道

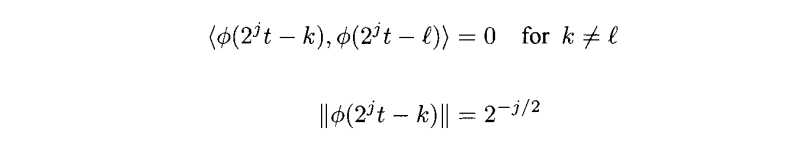
我们可以用这些去形成V_j里面的一组基。

主题3.2（Vj的正交基）Vj的正交基为

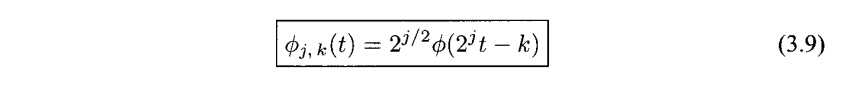
证明：我们从练习3.7可以看出Φ（2^jt-k）是线性无关的。所以任意位于V_j的函数都能表达成它们的线性组合。下面我们来证明正交性，如果k！=l我们有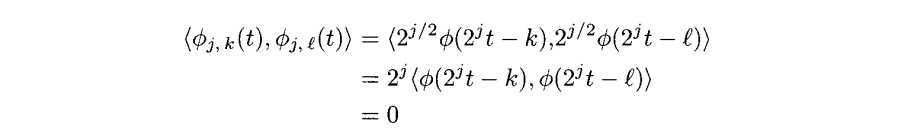

如果k=l，||Φj,k||²=2^j||Φ（2^jt-k）||²。在练习3.9（b）中知道||Φ（2^jt-k）||² 所以||Φj,k||²=1，因此{Φ_j,k（t）}是v_j的一组正交基。

我们来看一些Φ_j,k（t）的例子

例3.4 （画出Φj,k（t））请写出以下的函数的支撑集以及画出每个函数

解：

 以上四个函数在图3.8画出。由于此题过于简单，我们直接给出算式以及答案，不再过多说明

(a)

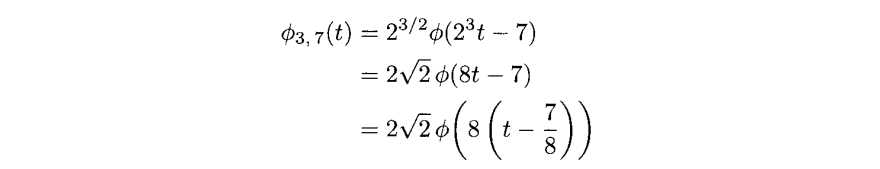
supp（Φ_3,7（t））=[7/8,1]

(b)

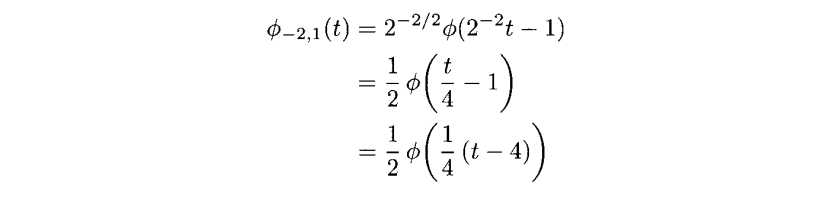
supp(Φ_-2,1（t）)=[4,8]

(c)

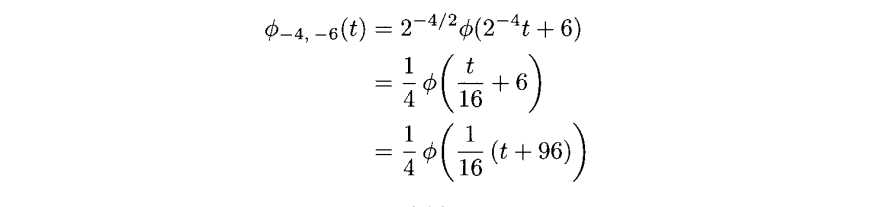
supp（Φ_-2,1（t））=[-96,-80]

(d)

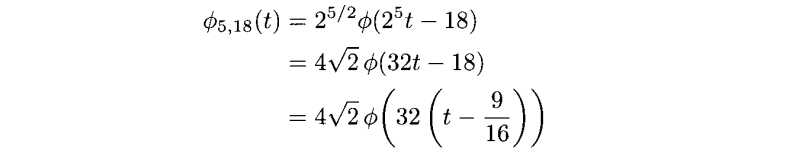
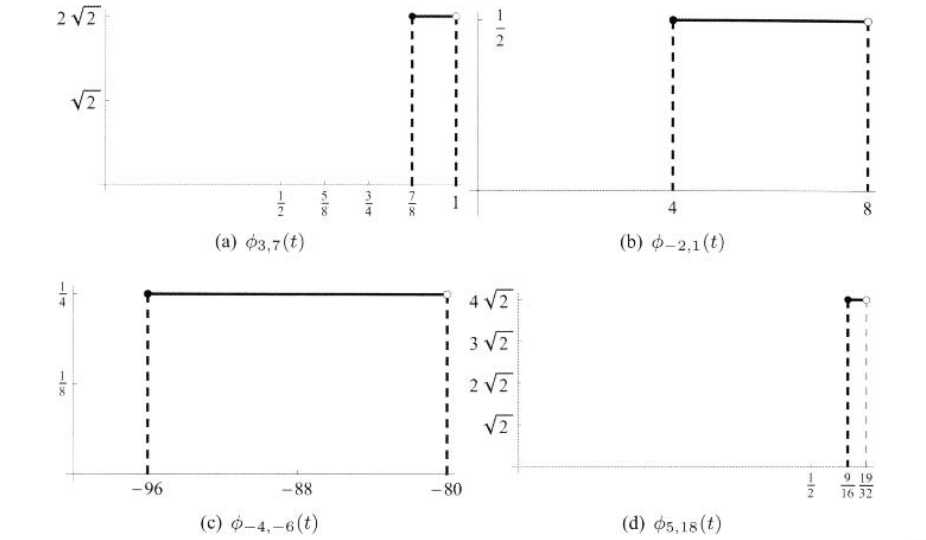
图3.8 3.4中的例子

• Φ_j，k（t）的支撑区间以及二元区间

主题3.3（Φ_j，k（t）的支撑区间）函数Φ_j，k（t）的支撑区间为

证明：留作练习3.11

对于我们的分析来说实在是非常重要的。因此我们对这个区间定义一个新的概念

定义3.3（二元区间I_jk）我们定义区间I_j,k（j,k∈Z）为

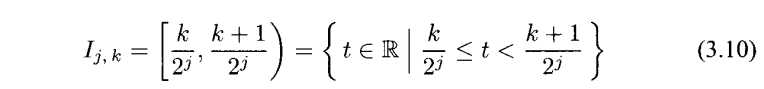
我们将第一个参数j称为区间水平。

词语“二元”表明这个区间是由两个参数组成的。我们来看一些I_j,k的例子

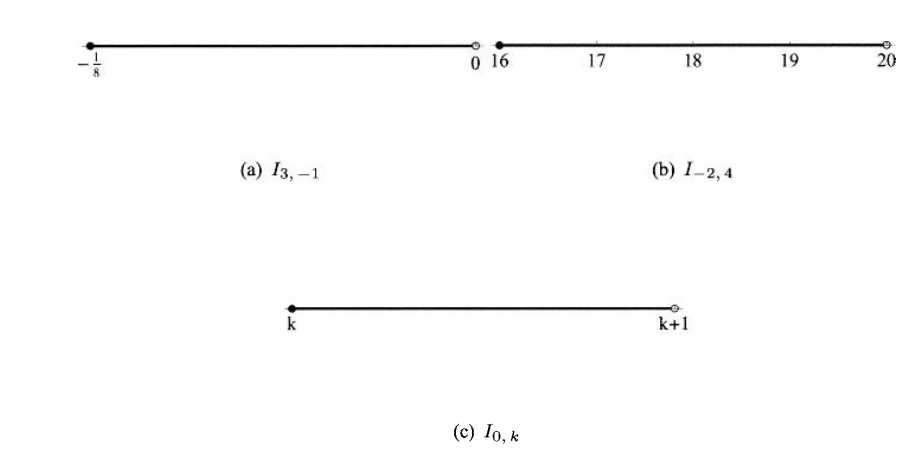
例3.5（区间I_j,k的例子）简述下列区间

解：

对于（a），我们有，区间（b）为，c为。每一个的区间如下图所示

我们对以下的两种二元间隔特别感兴趣，他们分别是

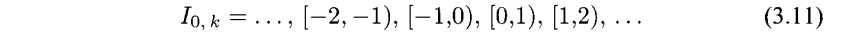
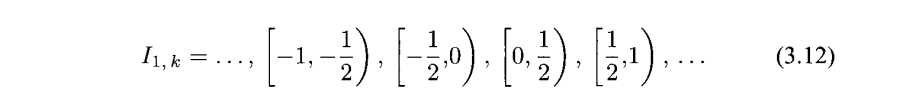
从上面的式子可以看出，这些区间都是不相交的，下面的性质就是说，如果你将他们都并起来将会是实数集R。

主题3.4（二元区间的并集）令

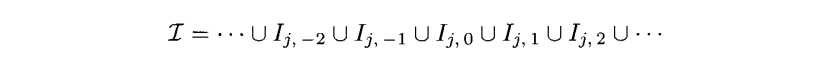
则 。

证明：因为τ是从R衍生出来的，我们有。现在如果要证明这个命题，我们就要证明。那么，我们现在设t∈R，并且集中研究2^jt。

我们总可以找到一个k来使得。（作者注：如果读者学过数理分析我们可以通过阿基米德公理来证明K的存在，详见Bartle和Sherbert的书）

那么现在我们将等式两边除以2^j，得到，这就证明了t∈I_j,k 。所以，证毕。

下面的主题就是来说明任意区间水平相等的不同区间不会相交

主题3.5（相同区间水平的二元间隔）对于k！=m，则有

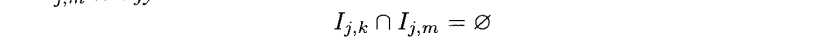
证明：留作练习3.14

这个主题告诉了我们同水平的区间之间的关系。下一个主题将告诉我们不同水平区间的关系

主题3.6（不同区间水平的二元间隔）假设l>j，他们的关系要么是或者

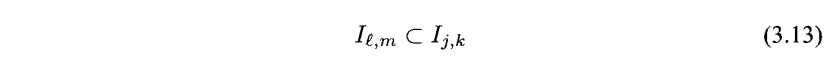
在（3.13）的情况

 证明： 我们分为两种情况来讨论，第一种是，这种情况已经包含在我们的命题里面了，所以我们考虑另一种情况。

现在我们只需要证明这一种情况是符合（3.13）的情况即可。

因为l>j，我们有，以及。因为是分分别为区间的长度。同时，又因为 1/2^l起码是1/2^j的一半。因此，I_l,m的长度最多是I_j,k的一半。

下面我们再分为两种情况。第一种情况（i）区间的左端点位于区间I_j,k内，也就是，第二种情况（ii）是区间的右端点位于区间I_j,k内。我们只证明第一种情况，将第二种情况的证明留作练习3.15。

我们不妨对其再一步的细分，如果端点在这个区间I_j,k左半部分，如图3.10所示，同时，我们得到以下的式子

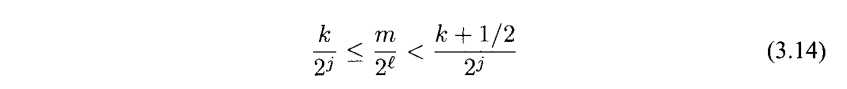
对它进行进一步的化简

图3.10 m/2^l在I_j,k 的左半区间

下面我们需要证明的是（m+1）/2^j 比（k+1）/2^j+1 小就可以了。我们从式子（3.15）说起。因为2^l-j>2所以不等式最右端变为(2k+1)/2^l,无论m取和值，m+1的值总是比2k+1的值要小，所以命题得证。另一种情况也是相似的，我们不再赘述。

（译者注：本文相对于原文略有修改，相信各位读者不难想象这个性质，因为无论区间以及下标都必须是整数，并且，大的区间起码是小的区间的长度的两倍。而小的区间肯定有一个区间的右端点在大区间的中点处，又一定有一个区间在大区间的左（右）端点处。在l-k=1的情况下，这两个区间为同一区间，否则，这些区间的序号都在这两个包含端点的区间之间。有兴趣的读者可以根据译者这个思路进行证明）

• L2(R)在Vj里面的投影

我们可以与上一节的投影的概念类比，定义一个类似的投影的概念

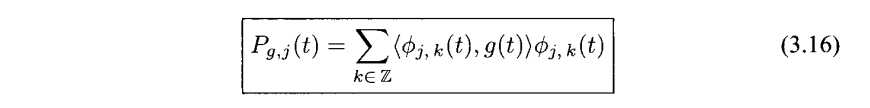
我们可以用（3.9）来表示（3.16）有

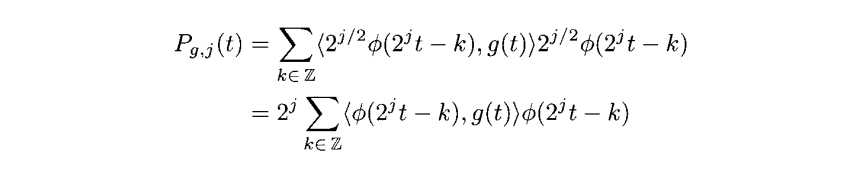
我们来举一些例子来发现它的一些性质

例3.6（在V_j上的投影） 我们采用例3.2中的函数g（t）来计算P_g，2（t）以及P_g,-1(t).

解：

我们先考虑第一种的情况

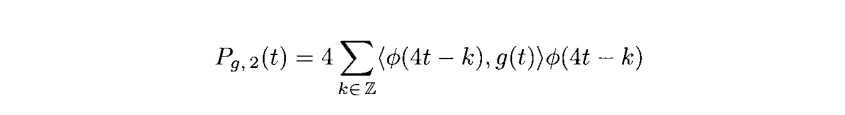
使用练习3.11的结果我们知道，因此，内积可以写作

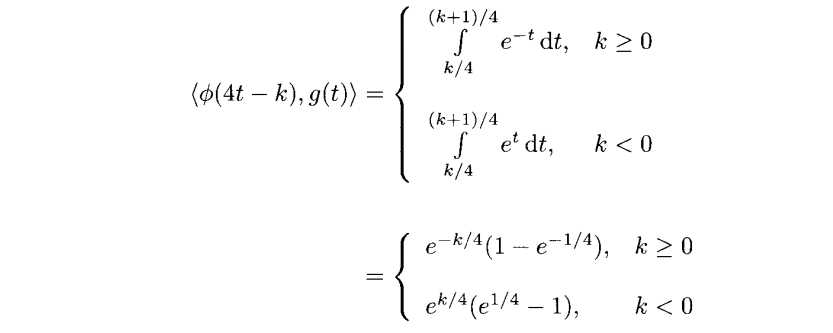
因此

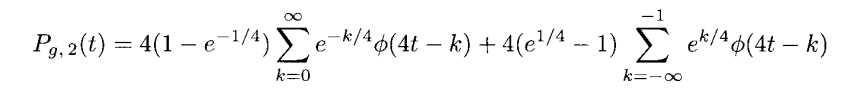
这个投影P_g,2（t）在图3.11（a）画出。我们继续考虑第二种情况

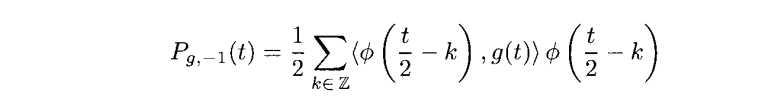
同样分析其支撑集，所以积分化为两种情况

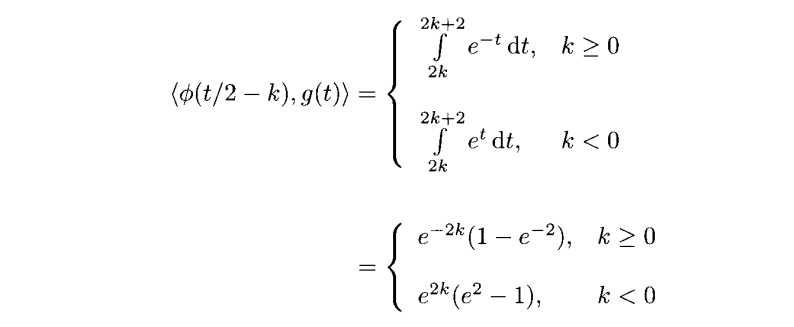
所以内积能写作

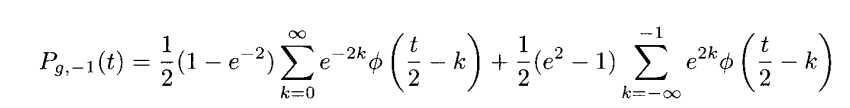
这个结果在图3.11（b）中画出

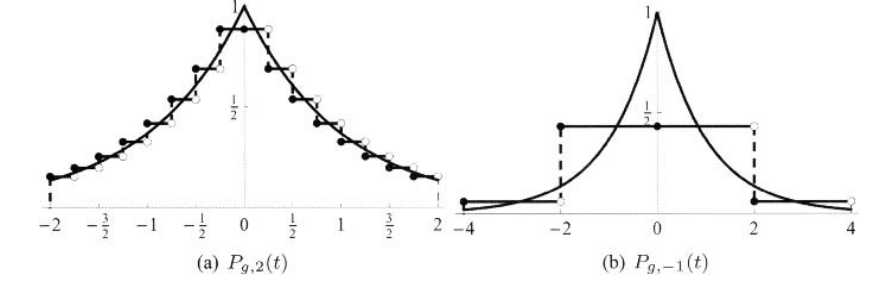
图3.11 例3.6中的函数在两个空间上的投影

• V_j的嵌套性质以及其他性质

V_j空间满足一种特殊的嵌套性质。例如，一个函数f（t）属于V0，它的常函数的分段点在于整数点处，同时，我们也可以认为它的分段点在（1/2）Z处，只不过，在中点分段和没有分段一样——为同一个数

因此，有下面的这个等式

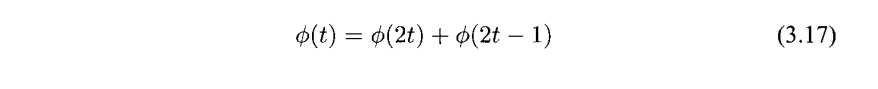
V0空间里面的元素可以视作V1空间的元素。假设

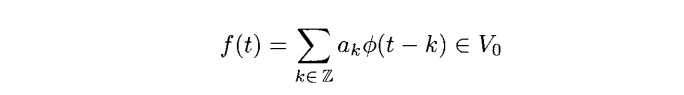
我们运用式子（3.17）对这个函数改写，如下

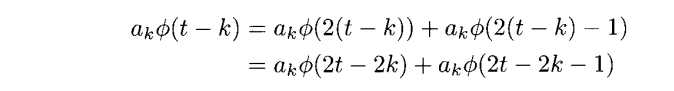
因此有

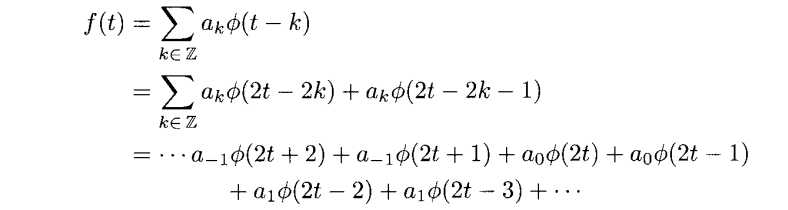
这就表示成为了V₁空间中的正交基的线性组合了，所以这个函数属于V₁空间。我们运用这个论点很容易能证明下面的性质。

性质3.7（V_j空间的嵌套性质） 对于（3.2）定义的V_j 空间有

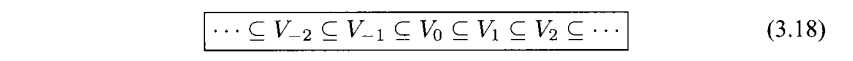
 证明：练习3.19

 Vj空间不仅仅是嵌套的，而且我们可以通过乘以系数2，来从一个空间变换到另一个空间。这个观点由下面的性质来阐述

性质3.8 （从一个Vj空间到另一个） 当且仅当函数f（2t）∈V_j+1时，函数f（t）∈V_j

证明：我们先假设f（t）∈V_j，从而要证明f（2t）∈V_j+1，而必要性论证留作练习3.20

首先f（t）∈V_j，那么这个函数能够表示成为Φ_j，k（t）的线性组合。

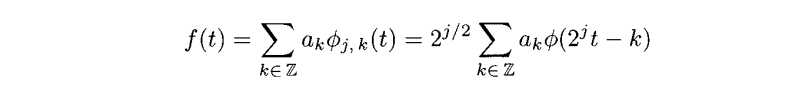
我们代入f（2t）

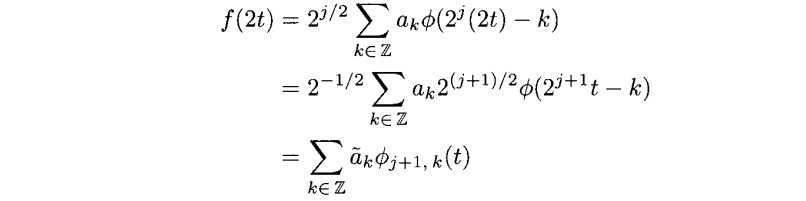
其中。因为我们能用Φ_j+1，k（t）的线性组合来表示f（2t），所以f（2t）∈Vj+1

这节的最后，我们用两个{V_j}_k∈Z最重要的性质来结束。

理论3.1（Vj空间的特性）哈尔空间满足以下两个性质

证明：这个定理的证明超出了本书的范围，因此有兴趣的读者可以去参考Frazier的书。（作者注：如果读者学过分析数学，这个问题实在是太简单了，如果读者尚未学习，我建议你去参加一个分析数学的课程并且重新审视在Frazier的书上给出的证明）

我们对理论3.1作一点说明。（3.19）说明的是，如果我们对所有的哈尔空间做交集，得出来是只包含唯一一个元素f（t）=0的集合。这是哈尔空间的分离性质。

我们可以通过口头证明（并不严谨的数学证明）来让读者更好的理解。（3.18）有

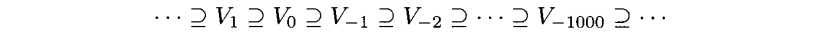
随着V_j空间的j趋向于-∞，倘若我们要采用V_j去拟合这个函数，如果f（t）不为0，始终有一个基函数是有值的，如果我们再对这个基函数的区间长度扩张至无穷。那么我们的拟合函数的能量将会趋向于无穷。因此，只有f（t）=0的函数能满足。

对于第二个式子，我们必须要先讨论并集的“栅"。”栅“表达的是并集的终止。一个集合V如果包含了他自己的极限点，我们就称这个集合是紧闭性的。也就是说如果{V_n}_n∈N是V，如果V_n的n趋近于∞，V_n仍属于V。但是如果趋向于无穷时不属于这个集合V，我们就称这个失闭点为V^-（上面有横线打不出来）。第二个性质说的就是任何函数g（t）∈L²（R），我们都能用公差不同的间断点的分段常函数的Vj来逼近它。使用嵌套性质，我们不难发现

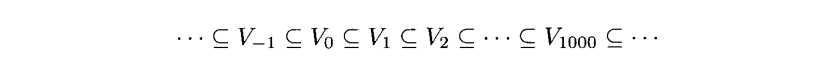
只要我们的分段足够的细，我们就能够得到足够好的精确度。

3.2 一般的哈尔空间Vj

标签：

原文地址：http://www.cnblogs.com/BIGShengun/p/5144795.html