标签:
最小生成树(Minimum Spanning Tree)
1:是一棵树(是一种特殊的图)
连通的,没有回路 有V 个顶点 一定有 V-1条边
2:生成树
包含了全部的顶点,所有的V-1条边 都在图里
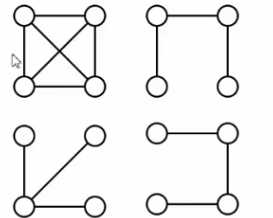 剩下的三个土 都是第一个完全图的生成树
剩下的三个土 都是第一个完全图的生成树
只要是 4个顶点 3条边 没有回路 就是生成树 这3个图 随便的加一条边 都会变成一个回路 也就不是 最小生成树了.
3:最小
边的权重之和最小
最小生成树存在 和 图连同 是充分必要条件
---------------------------------------------------------------------------------------------------------------------------
不论什么方法解决最小生成树问题都离不开 贪心算法
什么是贪 : 每一步都要最好的 .
什么是好 : 权重最小的边 .
需要约束:
只能用图里面的边.
只能刚好用掉V-1条边
不能有回路
贪心算法之一
Prim算法-让一颗小树长大
用Dijkstra算法和Prim算法比较一下感觉几乎一样
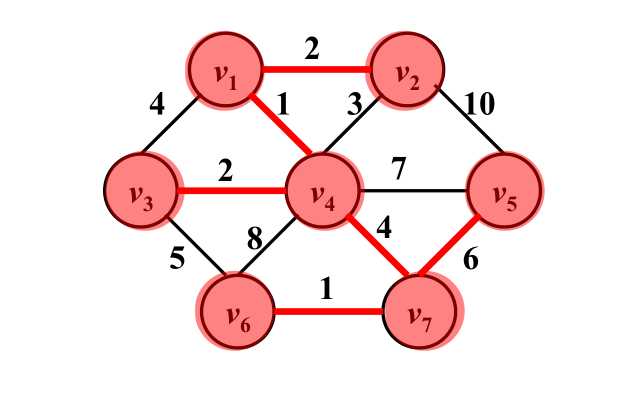
Prime算法 生成树的顺序是V1,V4,V2,V3,V7,V6,V5,
// Dijkstra算法
/*依鄙人之见,Dijkstra算法 就是走一个一定最小的步子,走完之后丈量一下去下一个地方需要多少步然后 给那个地方打上标签 这时候 可能会出现 A->B 为80 但是 A->C->B 为 5的情况 所以 在走完第一步之后 在第一部的基础上丈量完 然后走 离现在距离最近的点 这个点 该点一定没有 A 离源点近 但是改点是距离 A最近的 就这样 逐步求最小 不停的修改 */ void Dijkstra( Vertex s ) // 看来 再看一遍 写笔记 很重要 { while (1) { V = 未收录顶点中dist 最小者; if ( 这样的V在 不存在 ) break; collected[V] = true; for ( V 点 的每个邻接点 W ) if ( collected[W] == false ) if ( dist[V]+E <V,W> < dist[W] ) { dist[W] = dist[V] + E <V,W> ; path[W] = V; } } }
// Prim算法
void Prim() { MST=(s); while(1) { V=未收录顶点中dist最小者 // 和源点相邻的就是权重 . 剩下的是正无穷. if(都被收录了) break; dist[V]=0;//将V收录进MST for(V的 每个临接点W) { if(dist[W]!=0) //没有被收录 的话 { if(E(v,w)<dist[W]) { dist[W]=E(v,w); parent[W]=V; } } } } if(MST中的顶点不到V个) //就是 有独立的点 不连通的图. ERRor(生成树不存在) }
----------------图比较稀疏----------------
// Kruskal算法 //这个算法的核心就是 贪心了 将每一条边 一个一个的收录进去 (不能有回路)(变得个数是点的个数-1)void void Kruskal(Graph G) { MST={}; //生成一个空树 while(MST中不到V-1条边&&E中还有边) { 从E中取一条权重最小的边E(v,w); //用最小堆 将E(v,w)从E中删除; if(E(v,w)不再MST中构成回路) // 用并查集 将E(v,w)加入MTS; else 彻底无视E(v,w); } if(MST中不到V-1条边) Error("生成树不存在"); }
-----------最小生成树----------------
标签:
原文地址:http://www.cnblogs.com/A-FM/p/5153775.html